- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Основы алгебры логики
Содержание
- 1. Презентация к уроку Основы алгебры логики
- 2. Формы мышления. Законы логики отражают в сознании человека
- 3. Выделяют существенные признаки объекта, которые отделяют его
- 4. Свое понимание окружающего мира человек формулирует в
- 5. Умозаключение Умозаключения позволяют на основе известных фактов, выраженных
- 6. Алгебра высказываний. Алгебра высказываний разработана для того,
- 7. Логические операции над высказываниями.Логическое умножение (конъюнкция).Логическое сложение (дизъюнкция).Логическое отрицание (инверсия).Далее >>
- 8. Логическое умножение (конъюнкция).Составное высказывание, образованное в результате
- 9. Логическое сложение (дизъюнкция).Составное высказывание, образованное в результате
- 10. Логическое отрицание (инверсия). Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Слайд 2Формы мышления.
Законы логики отражают в сознании человека свойства, связи и отношения
Логика – наука о формах и способах мышления.
Первые учения о формах и способах рассуждения возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основу формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи) от его содержания.
Основные формы мышления – понятие, высказывание и умозаключение
Далее >>
Слайд 3 Выделяют существенные признаки объекта, которые отделяют его от других объектов. Например,
Понятие имеет две стороны: содержание и объем. Содержание – совокупность существенных признаков объекта. Объем – определяется совокупностью предметов, на которую он распространяется.
Понятие – это форма мышления, фиксирующая основные существенные признаки объекта.
Понятие
Далее >>
Слайд 4 Свое понимание окружающего мира человек формулирует в форме высказываний (суждений, утверждений).
Об объектах можно судить верно или не верно, то есть высказывание может быть истинным или ложным.
Истинное высказывание – то, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Например, истинное высказывание: «Солнце светит днем».
Ложное высказывание – то, которое не соответствует реальной действительности. Пример ложного высказывания: «Солнце светит ночью».
Иногда истинность того или иного высказывания является относительной. Истинность высказываний может зависеть от взглядов людей, от конкретных обстоятельств и так далее.
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть истинно или ложно.
Высказывание
Далее >>
Слайд 5Умозаключение
Умозаключения позволяют на основе известных фактов, выраженных в форме суждений (высказываний),
Примером умозаключения могут быть геометрические доказательства: если мы имеем суждение «Все углы треугольника равны», то путем умозаключения мы можем доказать, что в этом случае справедливо суждение «Этот треугольник равносторонний».
Посылками умозаключения по правилам формальной логики могут быть только истинные суждения.
Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Далее >>
К началу
Слайд 6
Алгебра высказываний.
Алгебра высказываний разработана для того, чтобы можно было определять
Истинному высказыванию соответствует значение логической переменной 1, а ложному значение 0
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: “истина”(1) и “ложь”(0)
Далее >>
Слайд 7Логические операции над высказываниями.
Логическое умножение (конъюнкция).
Логическое сложение (дизъюнкция).
Логическое отрицание (инверсия).
Далее >>
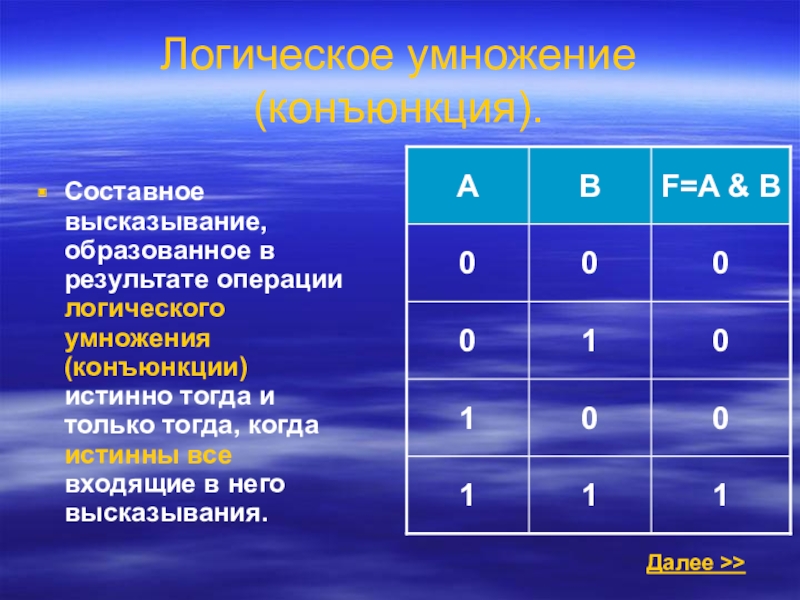
Слайд 8Логическое умножение (конъюнкция).
Составное высказывание, образованное в результате операции логического умножения (конъюнкции)
Далее >>
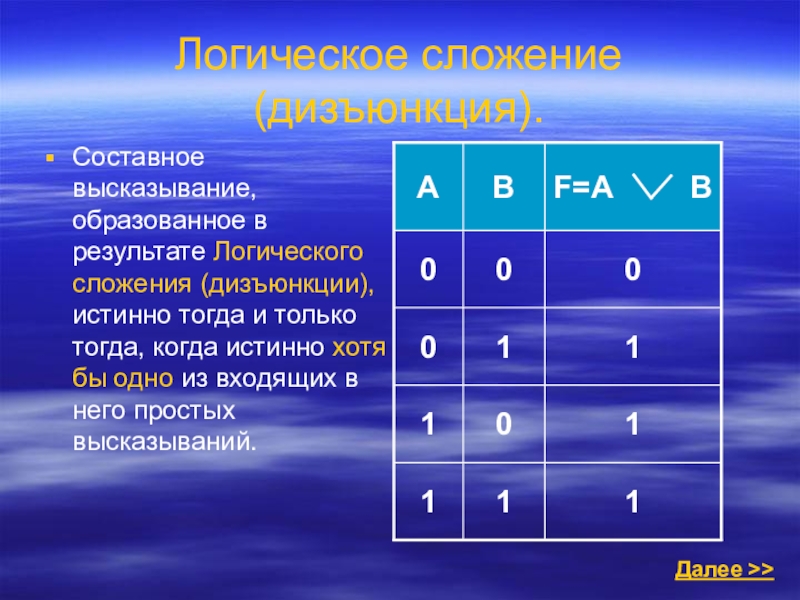
Слайд 9Логическое сложение (дизъюнкция).
Составное высказывание, образованное в результате Логического сложения (дизъюнкции), истинно
Далее >>
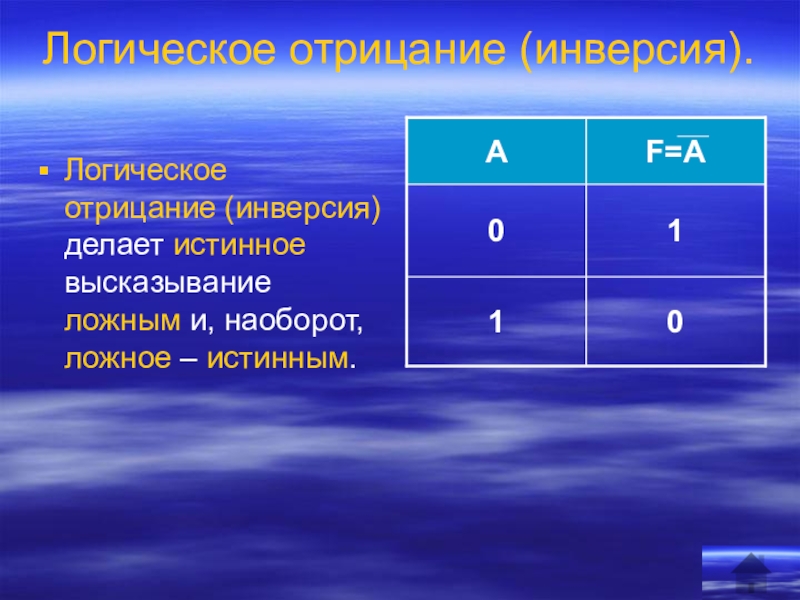
Слайд 10Логическое отрицание (инверсия).
Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот,