- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Моделирование экологических систем
Содержание
- 1. Презентация к уроку Моделирование экологических систем
- 2. Постановка задачиэкологической системе, состоящей из двух популяций
- 3. Популяция совокупность особей одного вида, существующих в одно и то же время на определенной территории.
- 4. Построение математической модели Пусть Ni –
- 5. Исследование экспоненциального роста начато еще Леонардо Фибоначчи
- 6. Скорость роста популяцииВ рассматриваемой системе «хищник-жертва» происходят
- 7. допущения1. При отсутствии хищников скорость роста численности
- 8. Составление списка параметров модели r — параметр
- 9. Вычислительный экспериментВходные параметры
- 10. Оформление программы1. Информационное поле с необходимыми пояснениями2. Начальные данные3. Расчеты4. График
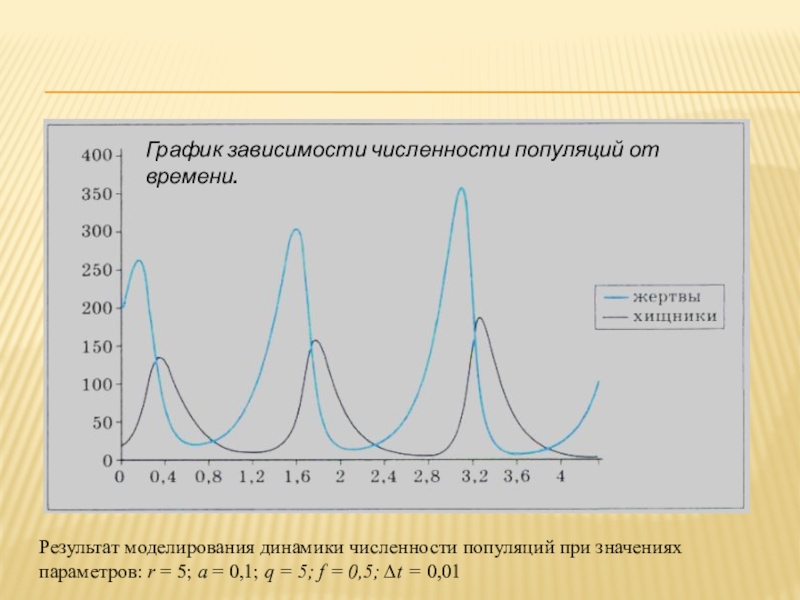
- 11. График зависимости численности популяций от времени.
- 12. Анализ полученных результатовПри каком соотношение размеров популяций,
- 13. область I — N возрастает, С убывает;область
Постановка задачиэкологической системе, состоящей из двух популяций живых организмов, одна из которых существует исключительно за счет поедания представителей другой. Такую систему принято называть «хищник-жертва». Например: волки и
Слайд 1математическое моделирование экологической системы
§3.4.5.
Подготовил учитель информатик
МОУ «Школа-лицей №1» г.Алушты
Успаленко Игорь Николаевич
Слайд 2Постановка задачи
экологической системе, состоящей из двух популяций живых организмов, одна из
которых существует исключительно за счет поедания представителей другой.
Такую систему принято называть
«хищник-жертва».
Такую систему принято называть
«хищник-жертва».
Например:
волки и овцы,
лисы и зайцы,
щуки и караси
Слайд 3Популяция
совокупность особей одного вида, существующих в одно и то же
время на определенной территории.
Слайд 4Построение математической модели
Пусть Ni – численность популяции жертв,
Сi — численность хищников в некоторый момент времени ti .
Шаг по времени ∆t — конечная величина. Примем t0 = 0 — начальный момент времени наблюдений;
ti = i ∆t, i = 1, 2, 3, ... .
Шаг по времени ∆t — конечная величина. Примем t0 = 0 — начальный момент времени наблюдений;
ti = i ∆t, i = 1, 2, 3, ... .
Слайд 5Исследование экспоненциального роста начато еще Леонардо Фибоначчи (1170–~1250) и Томасом Мальтусом
(1766–1834).
Численность популяции
Где DNi — это скорость изменения численности жертв, а
DCi — скорость изменения численности хищников.
Слайд 6Скорость роста популяции
В рассматриваемой системе «хищник-жертва» происходят процессы, способствующие как
росту
численности популяций (скорость — положительная величина),
так и убыванию численности (скорость — отрицательная величина).
так и убыванию численности (скорость — отрицательная величина).
Слайд 7допущения
1. При отсутствии хищников скорость роста численности популяции жертв пропорциональна DN
>0, r их количеству.
2. Вклад наличия хищников в скорость убывания популяции жертв пропорционален а произведению численностей обеих популяций.
3. При отсутствии пищи (жертв) скорость DCi <0 убывания популяции хищников пропорциональна q их численности.
4. Скорость роста популяции хищников благодаря поеданию жертв пропорциональна f произведению численностей обеих популяций — с поправкой на эффективность рождения потомства у хищников в результате поедания жертв.
2. Вклад наличия хищников в скорость убывания популяции жертв пропорционален а произведению численностей обеих популяций.
3. При отсутствии пищи (жертв) скорость DCi <0 убывания популяции хищников пропорциональна q их численности.
4. Скорость роста популяции хищников благодаря поеданию жертв пропорциональна f произведению численностей обеих популяций — с поправкой на эффективность рождения потомства у хищников в результате поедания жертв.
Слайд 8Составление списка параметров модели
r — параметр скорости роста популяции жертв
при отсутствии хищников (отражает допущение 1);
а — параметр эффективности поиска хищниками жертв (отражает допущение 2);
q — параметр скорости снижения популяции хищников при отсутствии пищи (отражает допущение 3);
f — параметр эффективности рождения потомства у хищников в результате поедания жертв (отражает допущение 4).
а — параметр эффективности поиска хищниками жертв (отражает допущение 2);
q — параметр скорости снижения популяции хищников при отсутствии пищи (отражает допущение 3);
f — параметр эффективности рождения потомства у хищников в результате поедания жертв (отражает допущение 4).
Слайд 9Вычислительный эксперимент
Входные параметры
N0 =
200, С0 = 25.
Параметры модели: г = 5; а = 0,1; q = 5; f = 0,5.
При вычислениях использовался
шаг по времени ∆t = 0,01.
Параметры модели: г = 5; а = 0,1; q = 5; f = 0,5.
При вычислениях использовался
шаг по времени ∆t = 0,01.
Выходные параметры
1. График зависимости численности популяций от времени.
Слайд 10Оформление программы
1. Информационное поле с необходимыми пояснениями
2. Начальные данные
3. Расчеты
4. График
Слайд 12Анализ полученных результатов
При каком соотношение размеров популяций, при котором численность, по
крайней мере, одной из них остается неизменной?
DNi = rNi – aCiNi = 0
— условие стабилизации Ni. жертв
— условие стабилизации Сi. хищников
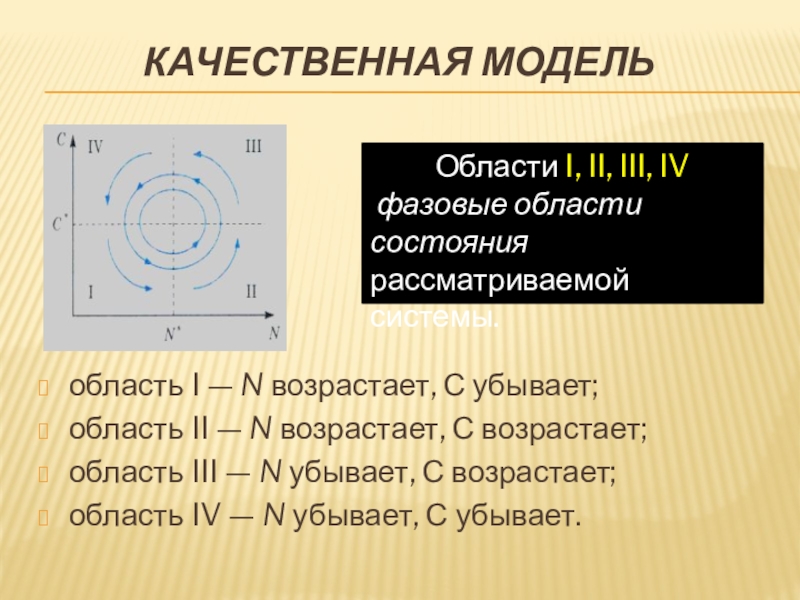
Слайд 13область I — N возрастает, С убывает;
область II — N возрастает,
С возрастает;
область III — N убывает, С возрастает;
область IV — N убывает, С убывает.
область III — N убывает, С возрастает;
область IV — N убывает, С убывает.
Качественная модель
Области I, II, III, IV
фазовые области состояния рассматриваемой системы.
