информатики ГБОУ лицей №144 Калининского района Санкт-Петербурга
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку информатики по теме Моделирование геометрических операций и фигур
Содержание
- 1. Презентация к уроку информатики по теме Моделирование геометрических операций и фигур
- 2. .
- 3. Слайд 3
- 4. Около любого правильного многоугольника можно описать окружность,
- 5. В среде графического редактора научиться моделировать геометрические объекты с заданными свойствами.
- 6. Геометрическая фигура характеризуется длинной сторон и углами,
- 7. Слайд 7
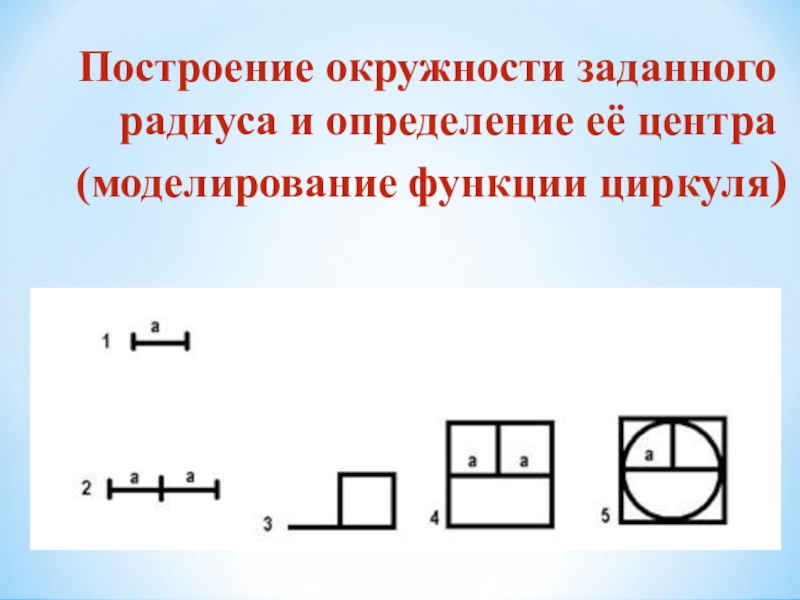
- 8. Построение окружности заданного радиуса и определение её центра (моделирование функции циркуля)
- 9. Разработка моделиКомпьютерный эксперимент
- 10. Задача №1. Построение правильного шестиугольника и треугольника.Согласно
- 11. Задача №2. Построение правильного четырехугольника и восьмиугольника.Пусть
- 12. ставший олицетворением Возрождения в Германии приводит теоретически
- 13. Задача 3. Приближенное построение правильного пятиугольника способом
- 14. А так ли уж важно изучать и
- 15. Слайд 15
- 16. Повторить материал по теме «Моделирование». Найти 3-4 примера правильных многоугольников в природе.Домашнее задание
- 17. Рефлексия
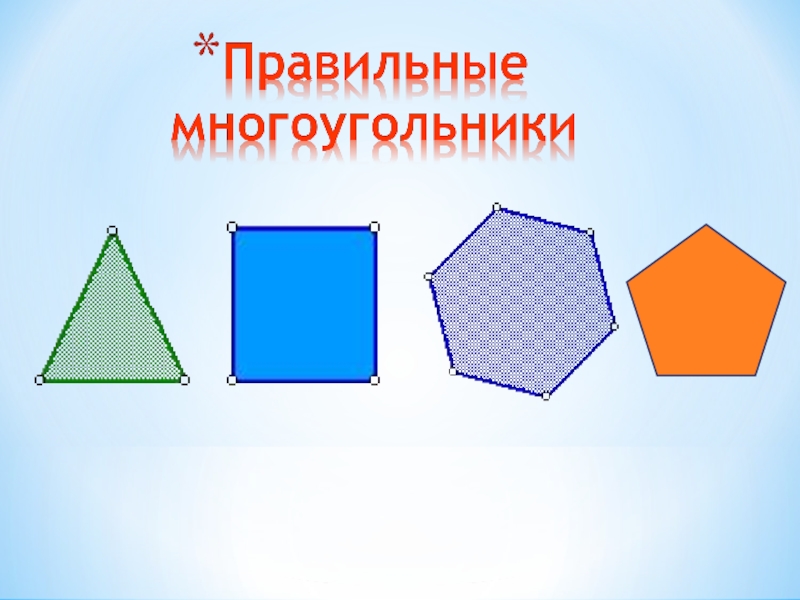
Около любого правильного многоугольника можно описать окружность, и притом только одну, и также в любой правильный многоугольник можно вписать окружность, и притом только одну. Центры описанной около правильного многоугольника и вписанной в него окружностей совпадают. Правильные
Слайд 1«Моделирование геометрических
операций и фигур»
16 марта 2015 года
Иванова Ирина Борисовна, учитель
Слайд 4Около любого правильного многоугольника можно описать окружность, и притом только одну,
и также в любой правильный многоугольник можно вписать окружность, и притом только одну.
Центры описанной около правильного многоугольника и вписанной в него окружностей совпадают.
Правильные многоугольники всегда выпуклые
Любой правильный многоугольник можно наложить сам на себя так, чтобы одна из двух произвольно заданных сторон совпала с другой; то же верно для любых двух его вершин. И обратно: многоугольник, обладающий обоими этими свойствами, правильный.
Имеется 2n способов совместить правильный n-угольник сам с собой: половина из них - повороты вокруг одной и той же точки, его центра, на углы, кратные360°/ n, вторая половина - n симметрий относительно прямых, соединяющих центр с вершинами и серединами сторон.
Центры описанной около правильного многоугольника и вписанной в него окружностей совпадают.
Правильные многоугольники всегда выпуклые
Любой правильный многоугольник можно наложить сам на себя так, чтобы одна из двух произвольно заданных сторон совпала с другой; то же верно для любых двух его вершин. И обратно: многоугольник, обладающий обоими этими свойствами, правильный.
Имеется 2n способов совместить правильный n-угольник сам с собой: половина из них - повороты вокруг одной и той же точки, его центра, на углы, кратные360°/ n, вторая половина - n симметрий относительно прямых, соединяющих центр с вершинами и серединами сторон.
Слайд 5В среде графического редактора научиться моделировать геометрические объекты с заданными свойствами.
Слайд 6
Геометрическая фигура характеризуется длинной сторон и углами, которые необходимо задать в
виде отрезков и углов на рабочем поле графического редактора перед началом построения.
Слайд 8Построение окружности заданного радиуса и определение её центра (моделирование функции циркуля)
Слайд 10Задача №1. Построение правильного шестиугольника и треугольника.
Согласно формуле Аn= 2R*sin180°/n сторона
АВ правильного шестиугольника равна радиусу R описанной окружности. Поэтому, если задан произвольный отрезок PQ, то для построения правильного шестиугольника, стороны которого равны PQ, достаточно построить окружность радиуса PQ, взять на ней произвольную точку А и, не меняя раствора циркуля, отметить на этой окружности последовательно точки B, C, D, E, F так, чтобы AB=BC=…=EF=PQ. Проведя затем отрезки AB, BC, CD, DE, EF, FA, получим шестиугольник ABCDEF, который согласно теореме о правильном многоугольнике является правильным, причем его стороны равны отрезку PQ.
Выполнить построение равностороннего
треугольника по рисунку:
Группа 1
Слайд 11
Задача №2. Построение правильного четырехугольника и восьмиугольника.
Пусть w-данная окружность с центром
в точки О и радиусом R. Через точку О проведем диаметр АС и к этому диаметру проведем серединный перпендикуляр, который пересечет окружность w в двух точках В и D.Теперь последовательно соединим точки A,B,C и D. ABCD-искомый квадрат.
Для того, чтобы построить правильный восьмиугольник нужно сначала построить правильный четырехугольник, например, А1А3А5А7-квадрат, потом построить биссектрисы углов А1OА3, А3OА5, А5OА7, А7OА1, которые прересекут окружность в точках А2, А4, А6, А8 соответственно, затем последовательно соединить точки А1,А2,А3,А4,А5,А6,А7,А8. А1А2...А8-искомый восьмиугольник.
Для того, чтобы построить правильный восьмиугольник нужно сначала построить правильный четырехугольник, например, А1А3А5А7-квадрат, потом построить биссектрисы углов А1OА3, А3OА5, А5OА7, А7OА1, которые прересекут окружность в точках А2, А4, А6, А8 соответственно, затем последовательно соединить точки А1,А2,А3,А4,А5,А6,А7,А8. А1А2...А8-искомый восьмиугольник.
Группа 2
Слайд 12
ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного
пятиугольника, заимствованный из великого сочинения Птолемея "Альмагест". Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия - в планировке крепостей
Альбрехт Дюрер (1471-1527гг),
Слайд 13
Задача 3. Приближенное построение правильного пятиугольника способом
А. Дюрера.
Приближенное построение правильного
пятиугольника представляет собой интерес. А.Дюрером оно проводится при условии неизменности раствора циркуля, что повышает точность построения. Способ построения описан Дюрером так:"Однако пятиугольник, построенный неизменным раствором циркуля, делай так. Проведи две окружности так, чтобы каждая из них проходила через центр другой. Два центра А и В соедини прямой линией. Это и будет стороной пятиугольника. Точки пересечения окружностей обозначь сверху С, снизу D и проведи прямую линию CD. После этого возьми циркуль с неизменным раствором и, установив одну его ножку в точку D, другой проведи через оба центра А и В дугу до пересечения её с обеими окружностями. Точки пересечения обозначь через E и F, а точку пересечения с прямой CD обозначь буквой G. Теперь проведи прямую линию через Е и G до пересечения с линией окружности. Эту точку обозначь Н. Затем проведи другую линию через F и G до пересечения с линией окружности и поставь здесь J.
Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник."
Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник."
Группа 3
Слайд 14А так ли уж важно изучать и знать сведения о правильных
многоугольниках?
В каких житейских ситуациях можно встретиться с правильными многоугольниками?
Историческая справка.
В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад. Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников, либо четыре квадрата, либо три правильных шестиугольник.
Вы не задумывались вот над таким вопросом: Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника?
Пчелы – удивительные творения природы. Свои геометрические способности они проявляют при построении своих сот. Если возьмем равносторонний треугольник, квадрат и правильный шестиугольник одинаковой площади (показываю модели), то периметр шестиугольника будет наименьшим. (Р3 = 45,9 см., Р4 = 40 см., Р6 = 37,8 см.).
Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек.
Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.
И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
В каких житейских ситуациях можно встретиться с правильными многоугольниками?
Историческая справка.
В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад. Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников, либо четыре квадрата, либо три правильных шестиугольник.
Вы не задумывались вот над таким вопросом: Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника?
Пчелы – удивительные творения природы. Свои геометрические способности они проявляют при построении своих сот. Если возьмем равносторонний треугольник, квадрат и правильный шестиугольник одинаковой площади (показываю модели), то периметр шестиугольника будет наименьшим. (Р3 = 45,9 см., Р4 = 40 см., Р6 = 37,8 см.).
Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек.
Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.
И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
Слайд 16Повторить материал по теме «Моделирование».
Найти 3-4 примера правильных многоугольников в
природе.
Домашнее задание