- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку информатики на тему Алгебра логики. Логическое высказывание. Основные логические операции (9 класс, учебник Семакина)
Содержание
- 1. Презентация к уроку информатики на тему Алгебра логики. Логическое высказывание. Основные логические операции (9 класс, учебник Семакина)
- 2. Логика. Основные понятияЛогика – наука о законах и
- 3. Логические операции1. Инверсия (отрицание)2. Конъюнкция (логическое умножение)3. Дизъюнкция (логическое сложение)4. Импликация (следование)5. Эквивалентность (равнозначность)
- 4. Инверсия (отрицание)Инверсия — это логическая операция, образующая
- 5. Конъюнкция (логическое умножение)Конъюнкция — это логическая операция,
- 6. Дизъюнкция (логическое сложение)Дизъюнкция — это логическая операция,
- 7. Импликация (следование)Импликация — это логическая операция, образующая
- 8. Эквивалентность (равнозначность)Эквивалентность — это логическая операция, образующая
- 9. Таблицы истинностиДля записи логических функций часто используют
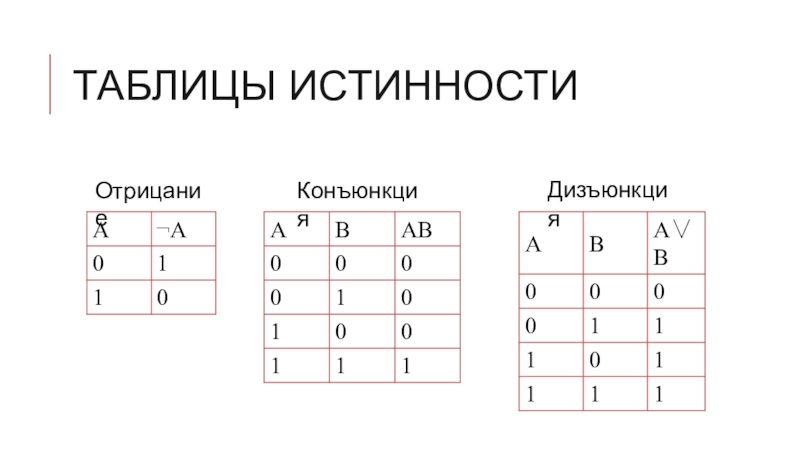
- 10. Таблицы истинностиОтрицаниеКонъюнкцияДизъюнкция
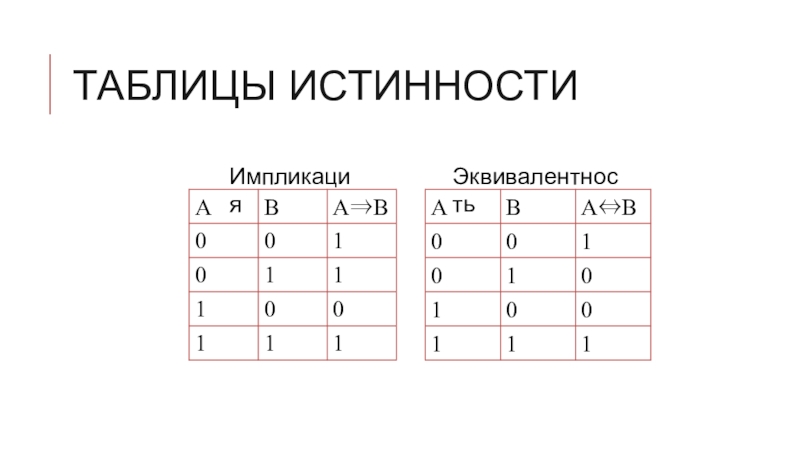
- 11. Таблицы истинностиИмпликацияЭквивалентность
Логика. Основные понятияЛогика – наука о законах и формах мышления.Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно.Утверждение – суждение, которое требуется доказать или опровергнуть.Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.Умозаключение – логическая
Слайд 2Логика. Основные понятия
Логика – наука о законах и формах мышления.
Высказывание (суждение) – некоторое
предложение, которое может быть истинно (верно) или ложно.
Утверждение – суждение, которое требуется доказать или опровергнуть.
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.
Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0).
Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
Утверждение – суждение, которое требуется доказать или опровергнуть.
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.
Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0).
Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
Слайд 3Логические операции
1. Инверсия (отрицание)
2. Конъюнкция (логическое умножение)
3. Дизъюнкция (логическое сложение)
4. Импликация
(следование)
5. Эквивалентность (равнозначность)
5. Эквивалентность (равнозначность)
Слайд 4Инверсия (отрицание)
Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда
и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или A.
Читается «НЕ» (например, «не А»).
В выражениях обозначается ¬A или A.
Читается «НЕ» (например, «не А»).
Слайд 5Конъюнкция
(логическое умножение)
Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда
и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б»)
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б»)
Слайд 6Дизъюнкция
(логическое сложение)
Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда,
когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б»)
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б»)
Слайд 7Импликация (следование)
Импликация — это логическая операция, образующая сложное высказывание, ложное тогда
и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ...ТО» (например, «если А, то Б»)
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ...ТО» (например, «если А, то Б»)
Слайд 8Эквивалентность (равнозначность)
Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда
и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
Слайд 9Таблицы истинности
Для записи логических функций часто используют таблицы истинности.
Таблица истинности —
таблица, в которой указаны значения логической функции для всех возможных комбинаций значений ее аргументов.