- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Арифметические операции
Содержание
- 1. Презентация к уроку Арифметические операции
- 2. Логическое сложение При сложении цифр двоичного кода перенос
- 3. 0101010 1010100111100011+
- 4. 0101010 101010Проверка: 26 25 24 23
- 5. 111011 + 111011100011110
- 6. Логическое умножение Операция умножения выполняется по обычной схеме,
- 7. 1001* 10100000100100001001+0010111
- 8. 1111* 11100000111111111111+000011
- 9. Логическое вычитание Вычитание чисел удобно осуществлять путем специального
- 10. Алгоритм преобразования положительного кода числа в отрицательный
- 11. 00000111 +1111110101110001111000111
- 12. Пример: 15 – 6 =
- 13. 00001111 +111110101100011111000111
- 14. Домашнее задание: § 16 [1] 10010011
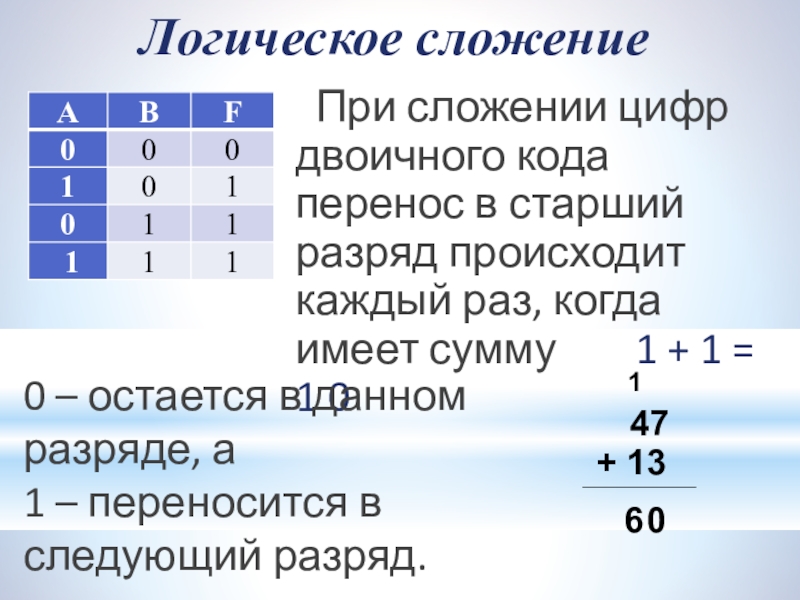
Слайд 2Логическое сложение
При сложении цифр двоичного кода перенос в старший разряд происходит
47
+ 13
0
6
1
0 – остается в данном разряде, а
1 – переносится в следующий разряд.
Слайд 40101010
101010
Проверка:
26 25 24 23 22 21 20
25 +
=32 + 8 + 2 = 42
26 + 24 + 22 =
= 64 + 16 + 4 = = 84
+
Слайд 6Логическое умножение
Операция умножения выполняется по обычной схеме, применяемой в десятичной с/с,
215
* 12
430
215
2580
+
с последовательным умножением множимого на очередную цифру множителя.
Слайд 7 1001
* 1010
0000
1001
0000
1001
+
0
0
1
0
1
1
1
* 10
90
Проверка:
26 + 24 + 23 + 21 = 64 + 16 + 8 + 2 = 90
Слайд 8 1111
* 1110
0000
1111
1111
1111
+
0
0
0
0
1
1
15
* 14
Проверка:
27 + 26 + 24 + 21 = 128 + 64 + 16 + 2 = 210
1
1
1
1
1
1
1
1
1
Слайд 9Логическое вычитание
Вычитание чисел удобно осуществлять путем специального преобразования кода, в результате
7 – 3 = 7 + ( - 3) = 4
Слайд 10Алгоритм преобразования положительного кода числа в отрицательный код
1. Код числа дописать
(3)10 = (00000011)2 – прямой код.
2. Используя логическое отрицание получаем обратный код числа (11111100)2.
3. К младшему разряду прибавляем – 1
11111100
+ 1
11111101 - дополнительный код числа(-3).
Слайд 12Пример: 15 – 6 = 15 + ( -
1. Код числа дописать до 8 бит
(6)10 = (00000110)2 – прямой код.
2. Используя логическое отрицание получаем обратный код числа (11111001)2.
3. К младшему разряду прибавляем – 1
11111001
+ 1
11111010 - дополнительный код числа (-6).
Слайд 14Домашнее задание: § 16 [1]
10010011
+ 101101
2.
3. Перевести в двоичную систему счисления числа и выполнить действие: 21 – 7 =
![Домашнее задание: § 16 [1] 10010011 + 1011012. 100001 * 1111 = 3. Перевести](/img/thumbs/fcd3ab527ecf42882c256dc95e94e73c-800x.jpg "Презентация к уроку Арифметические операции Домашнее задание: § 16 [1] 10010011 + 1011012. 100001 * 1111")
