- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Алгебра высказываний
Содержание
- 1. Презентация к уроку Алгебра высказываний
- 2. Алгебра наука об общих операциях, аналогичных сложению
- 3. ОбозначенияПростые высказывания в алгебре логики обозначаются заглавными
- 4. Логическая операция КОНЪЮНКЦИЯ (логическое умножение): ·
- 5. Таблица истинности конъюнкцииКонъюнкция - это логическая операция,
- 6. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):в естественном языке
- 7. Таблица истинности дизъюнкцииДизъюнкция - это логическая
- 8. Логическая операция ИНВЕРСИЯ (отрицание):в естественном языке соответствует
- 9. Таблица истинности ИНВЕРСИИ Отрицание
- 10. Логическая операция ИМПЛИКАЦИЯ (логическое следование):
- 11. Импликация - это логическая операция, ставящая в
- 12. Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность): · в естественном
- 13. Эквиваленция – это логическая операция, ставящая в
- 14. Логические операции имеют следующий приоритет:действия в скобках, инверсия, &, ∨, ⇒ , ⇔ .
- 15. Пример 3.6. Определите истинность составного высказывания: (А&В)
- 16. Определение истинности составного логического высказывания с использованием NumLock Calculator.
- 17. Слайд 17
- 18. Пример 3.7. Даны три числа в различных
- 19. Арифметические и логические операции с использованием Wise Calculator.
- 20. Пример 3.8. Какие из высказываний А, В,
- 21. 1. Выделите в составных высказываниях простые. Обозначьте
- 22. 2. Ниже приведена таблица, левая колонка которой
Слайд 2Алгебра наука об общих операциях, аналогичных сложению и умножению, которые могут
Алгебру логики интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.
Слайд 3Обозначения
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А =
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному — 0.
Таким образом, А = 1, В = 0.
Слайд 4Логическая операция КОНЪЮНКЦИЯ (логическое умножение):
· в естественном языке соответствует союзу
· в алгебре высказываний обозначение &;
· в языках программирования обозначение And
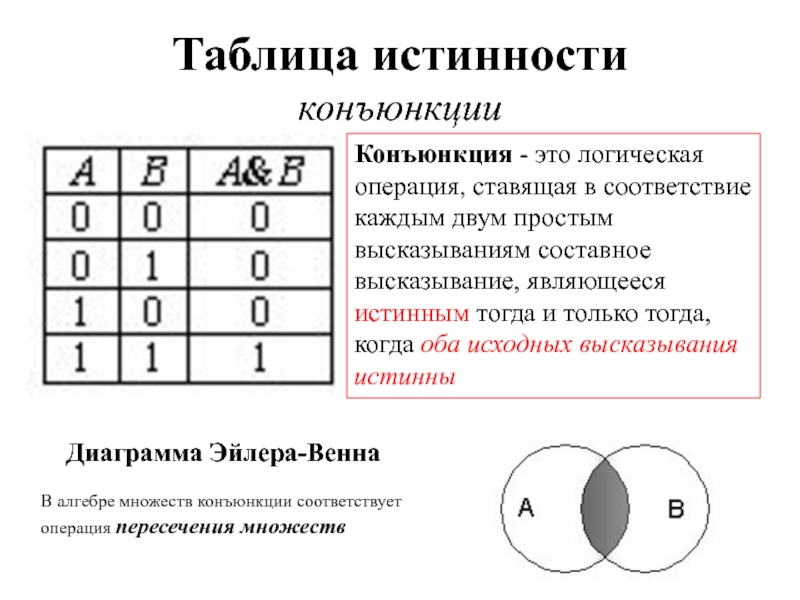
Слайд 5Таблица истинности
конъюнкции
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум
В алгебре множеств конъюнкции соответствует операция пересечения множеств
Слайд 6Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):
в естественном языке соответствует союзу или;
обозначение
в языках программирования обозначение Or.
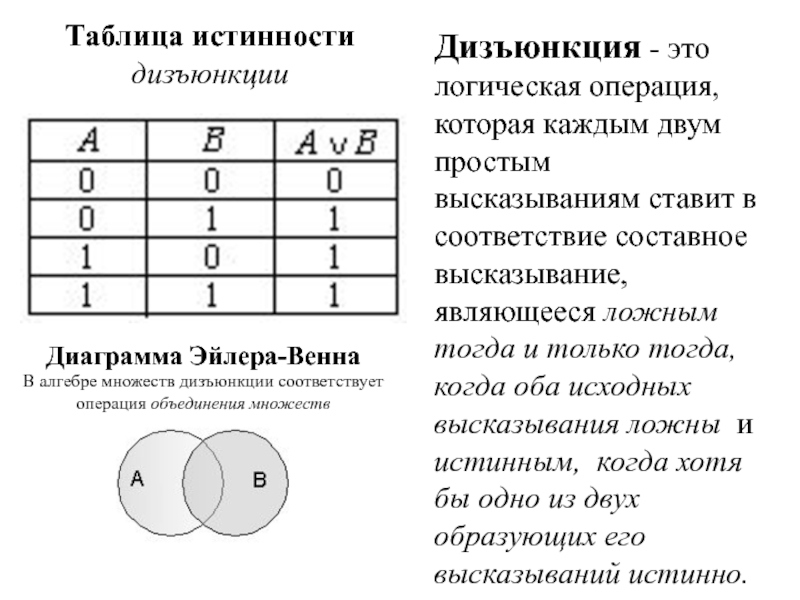
Слайд 7Таблица истинности
дизъюнкции
Дизъюнкция - это логическая операция, которая каждым двум простым
Слайд 8Логическая операция ИНВЕРСИЯ (отрицание):
в естественном языке соответствует словам неверно, что... и
обозначение ;
в языках программирования обозначение Not;
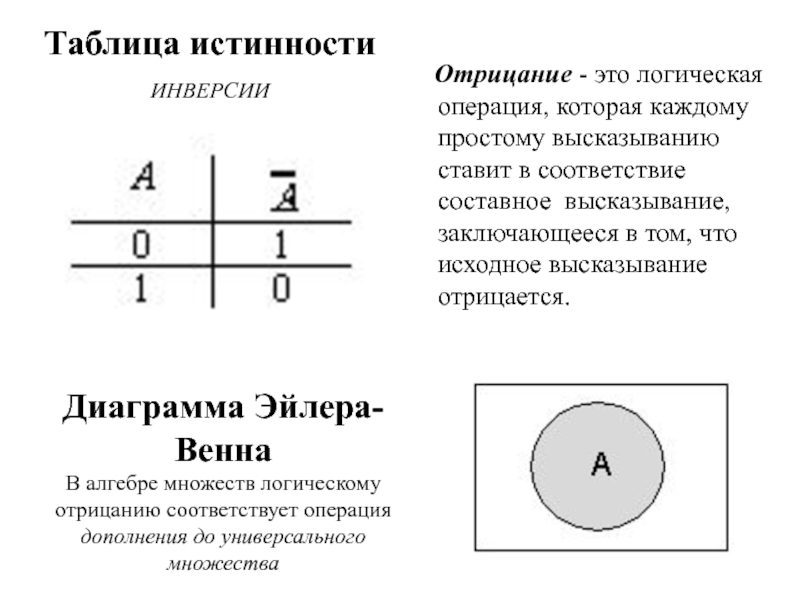
Слайд 9Таблица истинности
ИНВЕРСИИ
Отрицание - это логическая операция, которая
Слайд 10Логическая операция ИМПЛИКАЦИЯ
(логическое следование):
в естественном языке соответствует обороту если
обозначение ⇒ .
Слайд 11Импликация - это логическая операция, ставящая в соответствие каждым двум простым
Таблица истинности
ИМПЛИКАЦИИ
Слайд 12Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность):
· в естественном языке соответствует оборотам речи
· обозначения ⇔ , ~ .
Слайд 13Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым
Таблица истинности эквиваленции:
Слайд 15Пример 3.6. Определите истинность составного высказывания: (А&В) & (C ∨D), состоящего
А = {Принтер – устройство вывода информации},
В = {Процессор – устройство хранения информации},
С = {Монитор – устройство вывода информации},
D = {Клавиатура – устройство обработки информации}.
Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний: А = 1, В = 0, С = 1, D = 0.
Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:
(1 & 0 ) &(1∨ 0) = (0&1) & (1∨ 0) = 0
Ответ: Составное высказывание ложно.
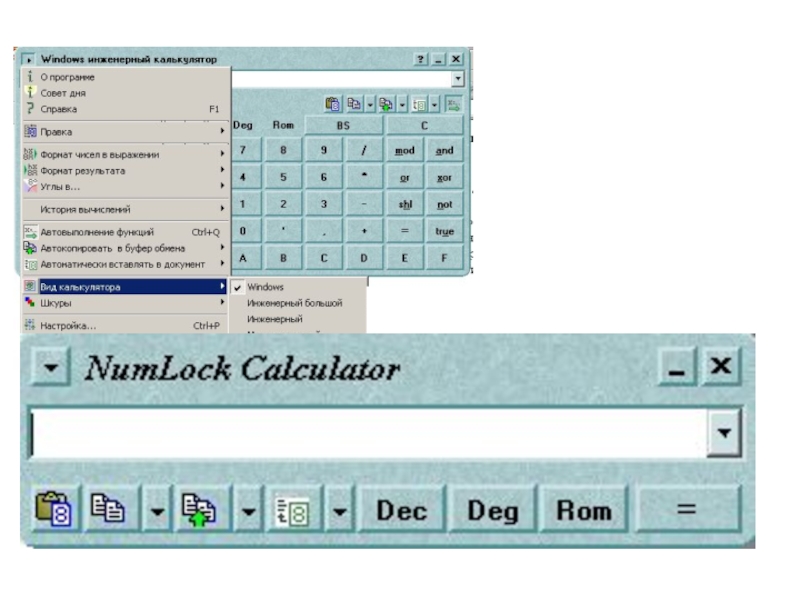
Слайд 16Определение истинности составного логического высказывания с использованием NumLock Calculator.
Слайд 18Пример 3.7. Даны три числа в различных системах счисления: А =
Слайд 20Пример 3.8. Какие из высказываний А, В, С должны быть истинны
Импликация ложна на единственном наборе логических значений (1, 0). Значит, ((A ∨ В)&В) = 1, С = 0.
Конъюнкция истинна на единственном наборе логических значений (1, 1). Значит, (A ∨ В) = 1 и В = 1.
Дизъюнкции истинна при наборах логических значений (0, 1) и (1, 1).
Ответ: существуют два набора логических значений, удовлетворяющих условию задачи: (А = 0, В = 1, С = 0) и (А = 1, В = 1, С = 0).
Слайд 211. Выделите в составных высказываниях простые. Обозначьте каждое их них буквой;
1) А = {Число 376 четное}, B = {Число 376 трехзначное}, А&B.
2) А = {Солнце движется вокруг Земли}, .
3) A = {Cумма цифр числа делится на 3}, B = {Число делится на 3}, А⇒ B.
4) А = {Число 15 делится на 3}, B = {Сумма цифр числа 15 делится на 3}, А⇔B.
1) Число 376 четное и трехзначное.
2) Неверно, что Солнце движется вокруг Земли.
3) Если сумма цифр числа делится на 3, то число делится на 3
4) Число 15 делится на 3 тогда и только тогда, когда сумма цифр числа 15 делится на 3.
Слайд 222. Ниже приведена таблица, левая колонка которой содержит основные логические союзы
А
А