- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Алгебра логики
Содержание
- 1. Презентация к уроку Алгебра логики
- 2. Готфрид Вильгельм Лейбниц (1646-1716) немецкий учёный
- 3. Понятие — форма мышления, которая выделяет существенные
- 4. ВЫСКАЗЫВАНИЯПростые(содержат только одну простую мысль) «Петров –
- 5. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ1. Отрицание (инверсия) «НЕ»
- 6. 4. Логическое следование (импликация) «ЕСЛИ … ТО»
- 7. Задания для закрепления пройденного материала:Упражнение 1:
- 8. Из данных предложений выберите те, которые являются
- 9. В приведенных предложениях вместо многоточий поставьте по
- 10. Задания : В следующих высказываниях выделите простые,
- 11. Поедем на дачуХорошая погодаПо прогнозам синоптиков предполагаются
- 12. Сегодня, завтра или через месяц он напишет
- 13. А12. Из двух высказываний «дядя Федор и
Слайд 2Готфрид Вильгельм Лейбниц (1646-1716) немецкий учёный и философ - основатель математической
Создал одну из первых механических вычислительных машин, которая могла складывать, вычитать, умножать, делить и извлекать квадратные корни.
Ступенчатый вычислитель Лейбница
- прототип современных компьютеров.
Английский математик
Джордж Буль - (1815-1864)
основатель Алгебры логики.
В своих трудах описал алфавит, орфографию и грамматику для математической логики. Считается основоположником математической логики как самостоятельной дисциплины.
Аристотель (384-328 гг. до н.э.)
- основатель формальной логики.
Описал основные формы абстрактного мышления:
понятие, высказывание, умозаключение.
Основоположники науки
ЛОГИКА
Слайд 3Понятие — форма мышления, которая выделяет существенные признаки предмета (класса предметов),
Примеры: проливной дождь, круглый шар, новый компьютер.
Высказывание (суждение/утверждение) — это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-то утверждается или отрицается. Высказывание может быть истинным или ложным.
Истинное высказывание - правильно отражает реальную действительность. Значение его истинности = 1
Ложное - противоречит действительности. Значение его истинности = 0
Примеры: «У прямоугольника все углы прямые» (Истинное высказывание).
«Компьютер был изобретен в середине XIX века (Ложное высказывание).
Умозаключение — форма мышления, с помощью которого из одного или нескольких суждений получается новое суждение.
Пример: Из высказывания: «Равнобедренный треугольник тот, у которого все углы равны» можно путём умозаключений получить другое высказывание «Этот треугольник равносторонний».
Логика - это наука о формах и способах мышления
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ
Слайд 4ВЫСКАЗЫВАНИЯ
Простые
(содержат только одну простую мысль)
«Петров – врач»
«Петров – шахматист»
Составные
(содержат несколько
«Петров - врач и шахматист» «Петров – не врач и не шахматист»
В алгебре Буля простые высказывания обозначаются буквами латинского алфавита и называются логическими переменными.
Обозначив А = «Петров – врач»,
В = «Петров – шахматист», получим логические выражения (функции):
F(A,B) = А и В («Петров - врач и шахматист»)
F(A,B) = не А и не В («Петров – не врач и не шахматист»)
Значение логической функции можно определить с помощью таблицы истинности, в которой перечисляются все комбинации значений логических переменных, входящих в выражение, и определяются соответствующие значения логической функции F.
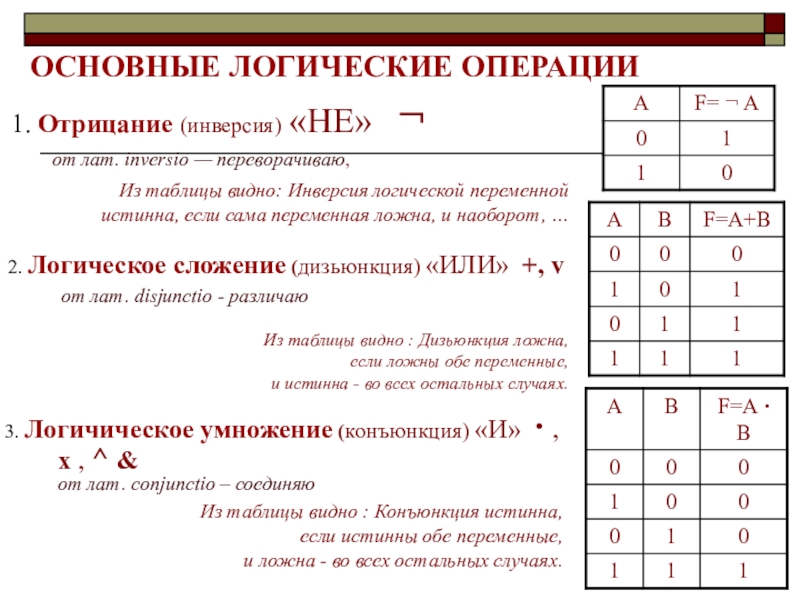
Слайд 5ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
1. Отрицание (инверсия) «НЕ» ¬
от лат. inversio
2. Логическое сложение (дизьюнкция) «ИЛИ» +, v
от лат. disjunctio - различаю
3. Логичическое умножение (конъюнкция) «И» ∙ , х , ^ &
от лат. conjunctio – соединяю
Из таблицы видно: Инверсия логической переменной истинна, если сама переменная ложна, и наоборот, …
Из таблицы видно : Дизьюнкция ложна,
если ложны обе переменные,
и истинна - во всех остальных случаях.
Из таблицы видно : Конъюнкция истинна,
если истинны обе переменные,
и ложна - во всех остальных случаях.
Слайд 64. Логическое следование (импликация) «ЕСЛИ … ТО» → от лат. implicatio
Из таблицы видно : Импликация ложна,
если из истины следует ложь,
и истинна - во всех остальных случаях.
5. Логическое равенство (эквивалентность/равнозначность)
«ТОГДА И ТОЛЬКО ТОГДА, КОГДА…» «НЕОБХОДИМО И ДОСТАТОЧНО » ≡ ↔
от лат. equivalents — равноценное
Из таблицы видно : Эквивалентность истинна,
если обе переменные одновременно либо истинны,
либо ложны.
Слайд 7Задания для закрепления пройденного материала:
Упражнение 1:
Запишите следующие высказывания в виде
Число 17 нечетное и двузначное.
Неверно, что корова - хищное животное.
Если число делится на 2, то оно - четное.
Если Маша - сестра Саши, то Саша - брат Маши.
Водительские права можно получить тогда и только тогда, когда тебе исполнится 18 лет.
Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдет на рыбалку
Слайд 8Из данных предложений выберите те, которые являются высказываниями, и обоснуйте свой
Наполеон был французским императором.
Чему равно расстояние от Земли до Марса?
Внимание! Посмотрите направо.
Электрон – элементарная частица.
Не нарушайте правил дорожного движения!
Полярная звезда находится в созвездии малой медведицы.
Не все то золото, что блестит.
Слайд 9В приведенных предложениях вместо многоточий поставьте по смыслу подходящие по смыслу
Для того, чтобы число делилось на 4, … чтобы оно было четным.
Для того, чтобы число делилось на 3, … чтобы оно делилось на 9.
Для того, чтобы число делилось на 10, … чтобы оно оканчивалось нулем.
Чтобы произведение двух чисел равнялось нулю, … чтобы каждое из них равнялось нулю.
Для того, чтобы сумма двух чисел была четным числом, … чтобы каждое из этих чисел было четным числом.
Чтобы четырехугольник был квадратом, … чтобы все его стороны были равны.
Слайд 10Задания : В следующих высказываниях выделите простые, обозначив каждое их них
а) Число 376 четное и трехзначное.
б) Зимой дети катаются на коньках или на лыжах.
в) Новый год мы встретим на даче либо на Красной площади.
г) Неверно, что Солнце движется вокруг Земли.
д) Если 14 октября будет солнечным, то зима будет теплой.
е) Земля имеет форму шара, который из космоса кажется голубым.
ж) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
Слайд 11Поедем на дачу
Хорошая погода
По прогнозам синоптиков предполагаются осадки в виде дождя
Сильный ветер
Отсутствие ветра
Плохая погода
Мы поедем на пляж
Антон приглашает нс в театр
Антон приглашает нас в цирк
После школы я буду учиться в институте
После школы я буду работать в интернет-центре
Из следующих простых высказываний составьте и запишите несколько сложных высказываний:
Слайд 12Сегодня, завтра или через месяц он напишет письмо
Если успешно закончишь первую
В школе уроки начнутся в 9 часов утра
Кончилось лето, и наступили прохладные дни
У меня есть старший брат
Каждое утро и каждый вечер он выходит на прогулку
После дождя трава мокрая
Круг – это не квадрат
Марс находится в пределах Солнечной системы
Распределите высказывания по типам (простое, сложное)
Слайд 13А12.
Из двух высказываний «дядя Федор и кот Матроскии не любят
Оба не любят молоко.
Оба любят Молоко.
Кот Матроскин любит Молоко, а дядя Федор нет.
дядя Федор любит молоко, а Кот Матроскин — нет.