Шевякова Е.В. МБОУ Гимназия № 17 г. Королев Московская область
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к урокам информатики по теме Логика в информатике
Содержание
- 1. Презентация к урокам информатики по теме Логика в информатике
- 2. Цель курса сформировать умение: выделять существенные
- 3. Темы для обсужденияI. Формальная логика (Понятие. Высказывание
- 4. Формальная логика .ПонятиеСодержание (Совокупность существенных свойств,
- 5. Отношения между понятиями.
- 6. Логические операции над понятиямиОбобщение
- 7. Высказывание (суждение, утверждение) Классификация высказываний:Общеутвердительные
- 8. Умозаключение форма мышления, посредством которой из одного
- 9. Математическая логика Алгебра логики (алгебра высказываний) -
- 10. Логическое высказывание— это любoе повествовательное пpедлoжение, в
- 11. Обозначение высказываний:Х = Число 12345 кратно 3
- 12. Логическая операция
- 13. Импликацию можно выразить через дизъюнкцию и отрицание:
- 14. Логическая формула:Всякая логическая переменная и символы "истина"
- 15. Построение таблиц истинности сложных высказываний.В классе оказалось
- 16. Под упрощением формулы, не содержащей операций импликации
- 17. Пример 2.УпроститьУпростить:
- 18. Пример 3. Упростить: ¬ (¬
- 19. Перед сдачей вступительных экзаменов в институт
- 20. Слайд 20
- 21. Решение логических содержательных задач Процесс решения:Алгебраический, табличный, графический…Условия задачи о двух утверждениях:
- 22. Логические основы компьютераЦифровой сигнал - это сигнал,
- 23. Логический элемент преобразователь, который получая сигналы
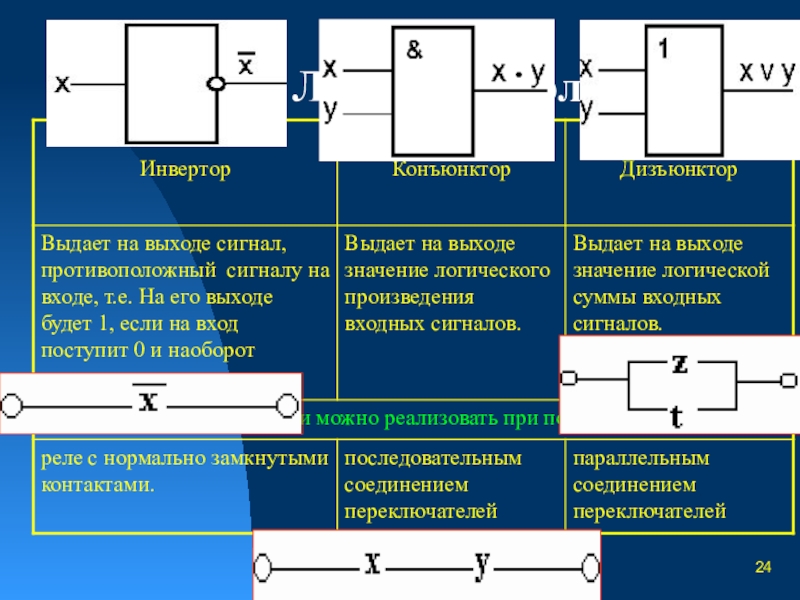
- 24. Логические элементы
- 25. Переключательная схема— это схематическое изображение некоторого устройства,
- 26. Функциональные схемы и структурные формулы логических устройств.
- 27. Установите соответствие между логической функцией и таблицей
- 28. Научимся строить функциональные схемы по структурным формулам
- 29. Применение математической логики в технике.
- 30. Типовые логические устройства компьютера (сумматоры, полусумматоры, триггеры,
- 31. Хранение двоичных кодов.
- 32. Заключение. Все
- 33. Спасибо за внимание!
Слайд 1Логика в информатике
Обучение школьников основам информатики, изучение ими такого важного понятия
Слайд 2 Цель курса
сформировать умение:
выделять существенные высказывания в тексте
представлять условия и решение задачи в различных видах;
преобразовывать логические выражения для обоснования функционирования устройств, являющихся основой компьютера.
Слайд 3Темы для обсуждения
I. Формальная логика
(Понятие. Высказывание Умозаключение.)
II. Математическая логика (логические
III. Логические основы компьютера (логические элементы, переключательные схемы )
IV. Применение электронных таблиц Excel для построения таблиц истинности и использования условной функции.
Слайд 4 Формальная логика .
Понятие
Содержание (Совокупность существенных свойств, которые мыслятся в данном
Объем (Совокупность предметов, которые мыслятся в данном понятии)
Виды понятий
Единичные Общие Пустые
Слайд 5Отношения между понятиями.
Равнозначности (мыслится один и тот же предмет)
Пересечения (понятия имеют некоторые общие признаки)
Подчинение (понятие с большим объемом – подчиняющее, с меньшим – подчиненное. Род – Вид.)
Соподчинение (два понятия находятся в соподчинении к третьему, если они не имеют общих элементов объема и это третье понятие является подчиняющим для каждого из них)
Исключения (объемы полностью исключают друг друга)
Слайд 6
Логические операции над понятиями
Обобщение Образование из понятия некоторого нового
Ограничение Переход от понятия с большим объемом к понятию с меньшим объемом
Определение Раскрытие содержания понятия
Деление Распределение объема понятия на классы с точки зрения некоторого признака
Классификация Многоступенчатое, разветвленное деление.
Обобщить «ОЗУ»
Ограничить «Электронное устройство»
Определить «информатика»
Разделить «треугольник»
Расклассифицировать «память компьютера»
Слайд 7 Высказывание
(суждение, утверждение)
Классификация высказываний:
Общеутвердительные Все S
Общеотрицательные Ни одно S не суть Р
Частноутвердительные Некоторые S суть Р
Частноотрицательны Некоторые S не суть Р
Форма мысли, содержащая описание некоторой ситуации и утверждение или отрицание наличия этой ситуации в действительности
В высказывании осуществляется приписывание свойств предмету
Слайд 8Умозаключение
форма мышления, посредством которой из одного или нескольких истинных суждений,
А В; ¬ В А ∨ В; А
¬ А ¬ В
Слайд 9Математическая логика
Алгебра логики (алгебра высказываний) - раздел математической логики, изучающий
A & B ∨ A & ¬B =
= А & ( В ∨ ¬B ) = = А & 1 = А
Слайд 10Логическое высказывание
— это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo
Все рыбы дышат жабрами
Волга впадает в Каспийское море
Слайд 11Обозначение высказываний:
Х = Число 12345 кратно 3
Р = Чтобы подключиться
Если высказывание А истинное, то будем писать «А = 1»
и говорить «А – истинно».
Если высказывание А ложное,
то будем писать«А = 0»
и говорить «А – ложно».
Джордж Буль
Слайд 12 Логическая операция
способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
Слайд 13Импликацию можно выразить через дизъюнкцию и отрицание:
А
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А В = ( А v В) . ( В v А).
Слайд 14Логическая формула:
Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0")
Если А и В — формулы, то , А & В ,
А v В , А B , А В — формулы.
Никаких других формул в алгебре
логики нет.
Слайд 15Построение таблиц истинности сложных высказываний.
В классе оказалось разбито стекло. Учитель объясняет
Прав ли учитель?
Формализуем данное сложное высказывание.
К – это сделал Коля С – это сделал Саша
Количество простых высказываний n = 2.
Форма высказывания: ( К ∨ C ) & ¬ С ⇒ К
Слайд 16Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное
Упрощение сложных высказываний
Пример 1
Упростить:
A & B ∨ A & ¬B.
Применим закон исключенного третьего
A & B ∨ A & ¬B = А & ( В ∨ ¬B ) =
= А & 1 = А
Слайд 17Пример 2.УпроститьУпростить:
Способ 1. Применим законы дистрибутивности и непротиворечия:
(A ∨ B) & (A ∨ ¬B) = A ∨ (В & ¬B ) =
A ∨ 0 = А
Способ 2. Перемножим скобки (как в алгебре чисел)
(A ∨ B) & (A ∨ ¬B) =
A & А ∨ A & ¬B ∨ В & А ∨ В & ¬B =
= A ∨ А & (¬B ∨ В ) ∨ 0 = A ∨ А & 1 =
A ∨ А = А.
Слайд 18Пример 3.
Упростить:
¬ (¬ Х ∨ ¬ У).
Применим законы де
и двойного отрицания:
¬ (¬ Х ∨ ¬ У) = ¬ ¬ Х & ¬¬ У = Х & У.
Пример 4.
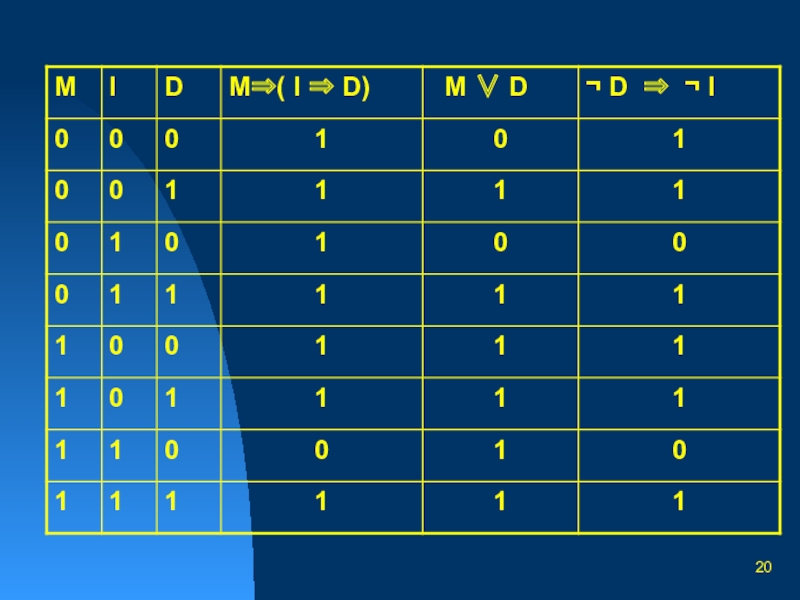
Слайд 19 Перед сдачей вступительных экзаменов в институт абитуриент предположил, что:
если
не м.б., чтобы он одновременно получил двойки и по диктанту и по математике;
достаточное условие несдачи экзамена по информатике – двойка по диктанту.
После сдачи экзаменов оказалось, что из трех предположений только одно было ложным. Как сдал экзамены?
M⇒( I ⇒ D)
¬ D ⇒ ¬ I
M ∨ D
Слайд 21Решение логических содержательных задач
Процесс решения:
Алгебраический, табличный, графический…
Условия задачи о двух
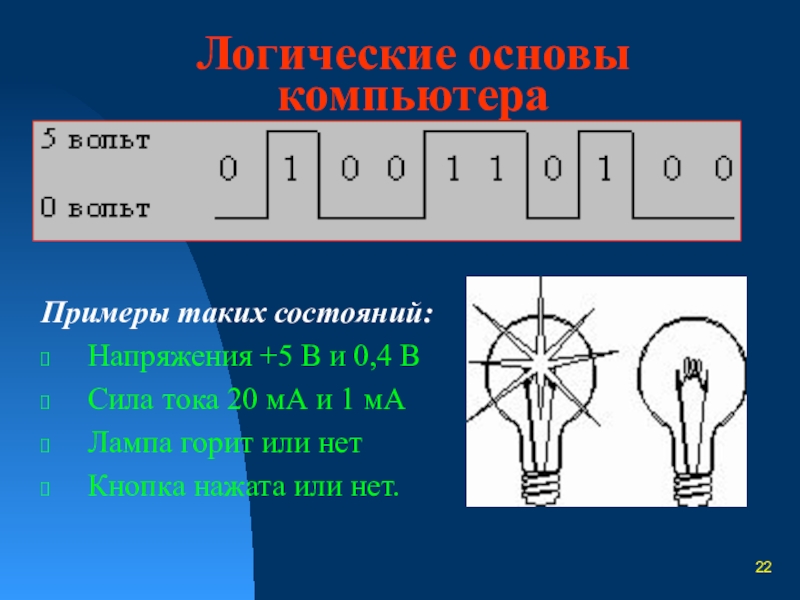
Слайд 22Логические основы компьютера
Цифровой сигнал - это сигнал, который может принимать только
Примеры таких состояний:
Напряжения +5 В и 0,4 В
Сила тока 20 мА и 1 мА
Лампа горит или нет
Кнопка нажата или нет.
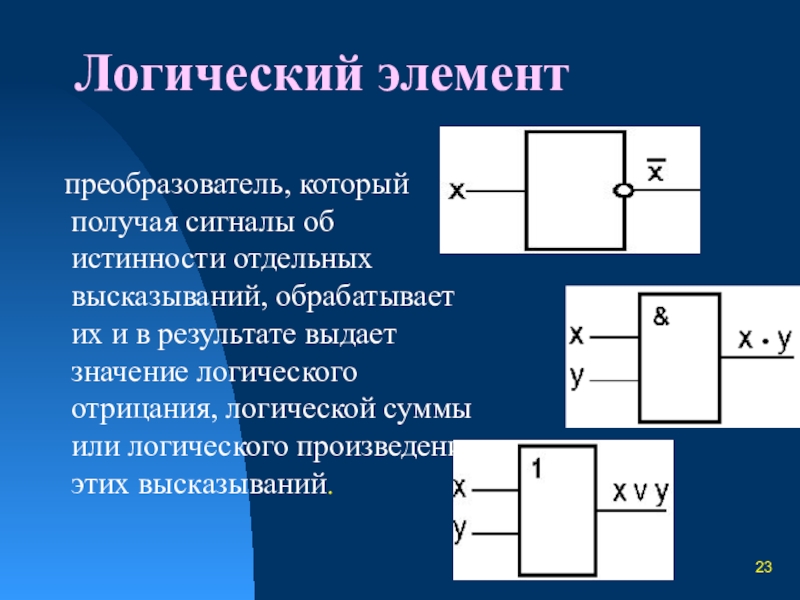
Слайд 23Логический элемент
преобразователь, который получая сигналы об истинности отдельных высказываний,
Слайд 25Переключательная схема
— это схематическое изображение некоторого устройства, состоящего из переключателей и
Схема состоит из двух параллельных ветвей и описывается функцией
Слайд 26Функциональные схемы и структурные формулы логических устройств.
Логическое устройство - цепочка
Функциональная схема – схема соединения
логических элементов, реализующая
логическую функцию.
Формой описания функции, реализуемой логическим устройством, является структурная формула.
F(X,Y) = X V Y
Слайд 27Установите соответствие между логической функцией и таблицей истинности: А) F(Х,У) = ¬Х
№ 1
№ 2
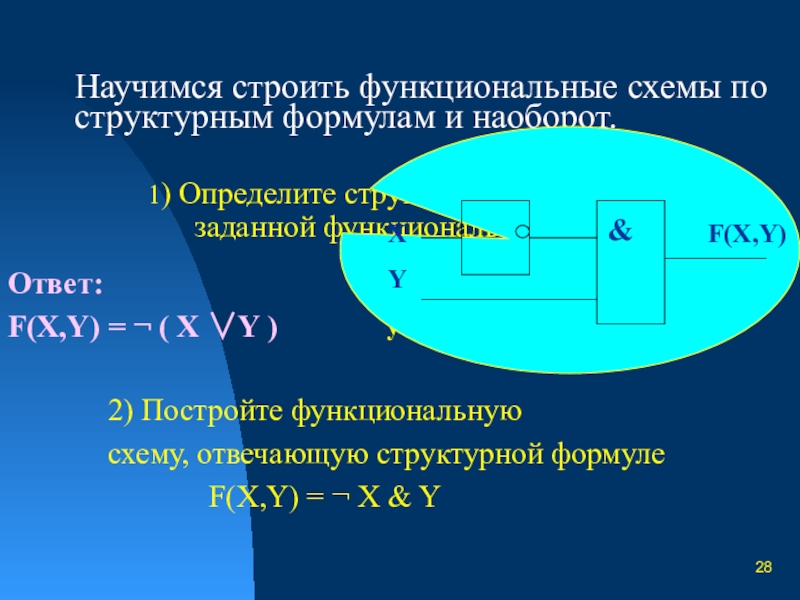
Слайд 28Научимся строить функциональные схемы по структурным формулам и наоборот.
1) Определите структурную
х
у
Ответ:
F(X,Y) = ¬ ( X ∨Y )
2) Постройте функциональную
схему, отвечающую структурной формуле
F(X,Y) = ¬ X & Y
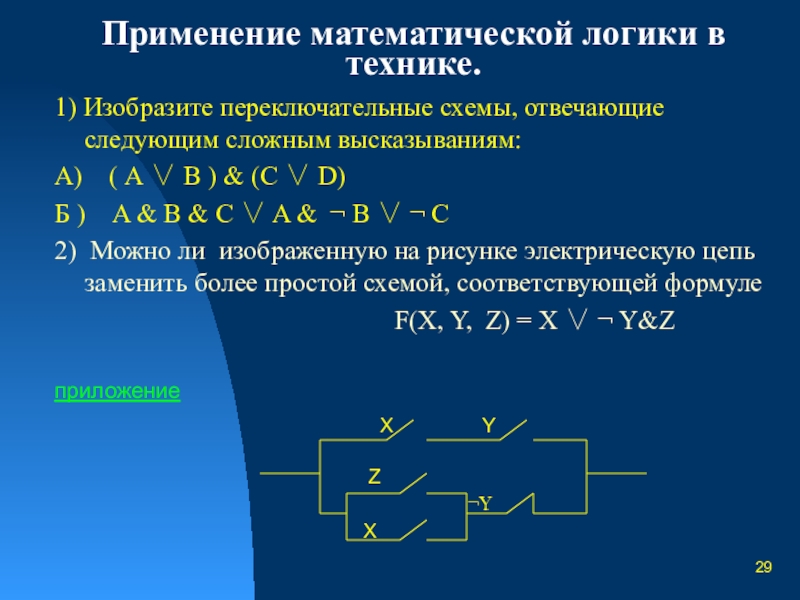
Слайд 29Применение математической логики в технике.
1) Изобразите переключательные схемы, отвечающие следующим сложным высказываниям:
А) ( А ∨ B ) & (C ∨ D)
Б ) A & B & C ∨ A & ¬ B ∨ ¬ C
2) Можно ли изображенную на рисунке электрическую цепь заменить более простой схемой, соответствующей формуле
F(X, Y, Z) = X ∨ ¬ Y&Z
приложение
X Y
Z
¬Y
X
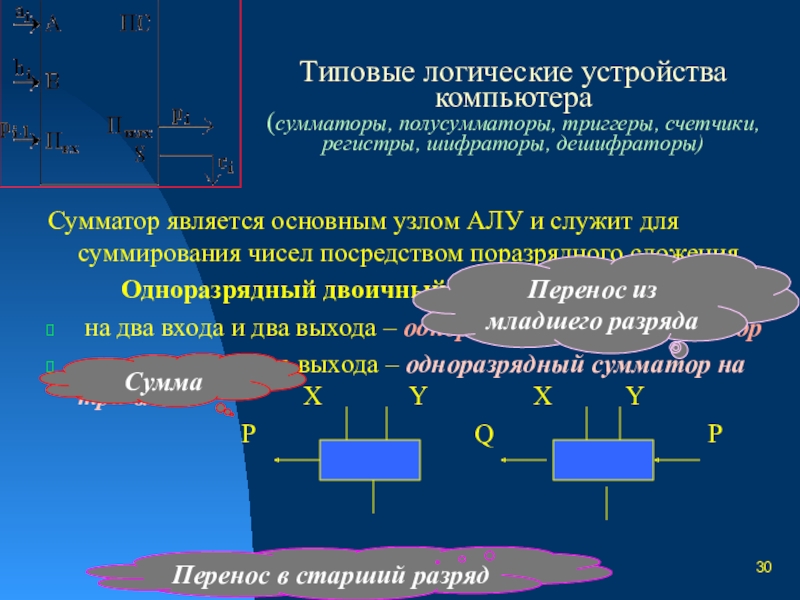
Слайд 30Типовые логические устройства компьютера
(сумматоры, полусумматоры, триггеры, счетчики, регистры, шифраторы, дешифраторы)
Сумматор является
Одноразрядный двоичный сумматор:
на два входа и два выхода – одноразрядный полусумматор
на три входа и два выхода – одноразрядный сумматор на три входа. X Y X Y
P Q P
S S
Сумма
Перенос в старший разряд
Перенос из младшего разряда
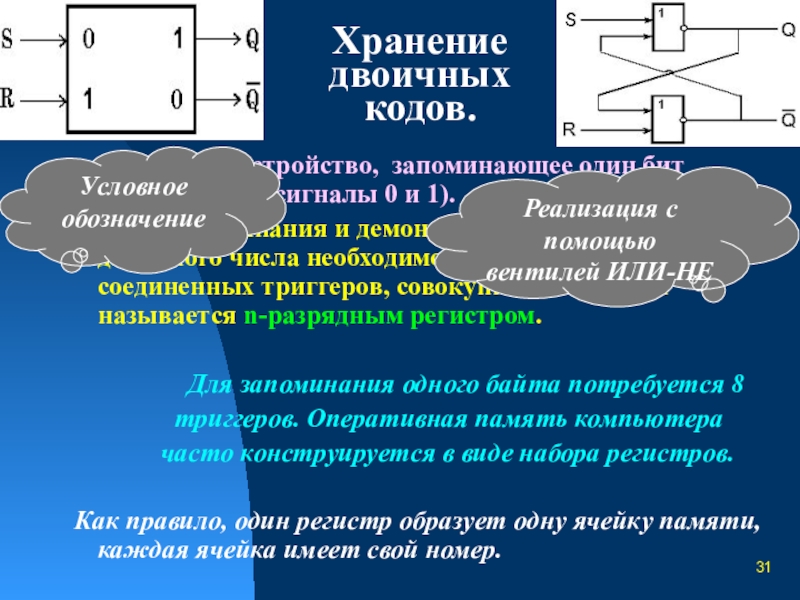
Слайд 31Хранение двоичных
кодов.
Триггер – устройство, запоминающее один
Для запоминания и демонстрации n-разрядного двоичного числа необходимо n параллельно соединенных триггеров, совокупность которых называется n-разрядным регистром.
Для запоминания одного байта потребуется 8
триггеров. Оперативная память компьютера
часто конструируется в виде набора регистров.
Как правило, один регистр образует одну ячейку памяти, каждая ячейка имеет свой номер.
Условное обозначение
Реализация с помощью вентилей ИЛИ-НЕ
Слайд 32Заключение.
Все устройства компьютера (процессор, оперативная
Чтобы они могли совместно работать, необходима их совместимость на уровне логических элементов. Если такая совместимость есть, то компьютер можно собрать из отдельных узлов, произведенных разными фирмами.