жизнь? – Игра!»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к мастер-классу Что наша жизнь? - Игра!
Содержание
- 1. Презентация к мастер-классу Что наша жизнь? - Игра!
- 2. Эдгар По «Говоря «мастерская игра», я имею
- 3. Теория игр занимается вопросами оптимального поведения людей при наличии противодействующего противника.
- 4. Комбинаторные игры
- 5. Пять уровней овладения мастерством игры: Знание
- 6. Правила игры Определено, какие бывают позиции в
- 7. Древняя китайская игра Ним (Камешки)
- 8. Дано:Игроков – 2.2 кучи камней: в 1-ой
- 9. Слайд 9
- 10. Выигрышные и проигрышные позиции.выигрышная позиция – это такая
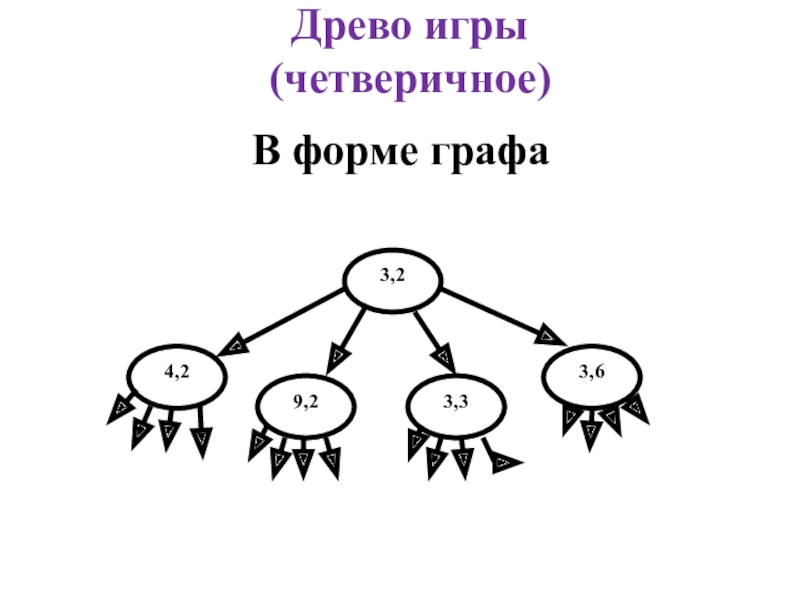
- 11. Древо игры (четверичное)В форме графа
- 12. В виде таблицы
- 13. Победа первого игрока:(3,2) – (4,2) – (5,2)
- 14. Слайд 14
- 15. Задача «Поиск фальшивой монеты»Дано: 12 монет.
- 16. Алгоритм Первое взвешивание.
- 17. Алгоритм Второе взвешивание.
- 18. Алгоритм Третье взвешивание.
- 19. Банка жизни
Эдгар По «Говоря «мастерская игра», я имею в виду ту степень совершенства, при которой игрок владеет всеми средствами, приводящими к победе».
Слайд 2Эдгар По
«Говоря «мастерская игра»,
я имею в виду ту степень
совершенства, при которой
игрок владеет всеми средствами,
приводящими к победе».
игрок владеет всеми средствами,
приводящими к победе».
Слайд 3Теория игр
занимается вопросами оптимального поведения людей при наличии противодействующего противника.
Слайд 5 Пять уровней овладения мастерством игры:
Знание правил игры и
владение основными ее стратегиями.
Способность учитывать в своей игре поведение соперников.
Интуитивная способность угадывать камни соперников.
Способность управлять удачей в игре.
Тайный уровень.
Способность учитывать в своей игре поведение соперников.
Интуитивная способность угадывать камни соперников.
Способность управлять удачей в игре.
Тайный уровень.
Слайд 6Правила игры
Определено, какие бывают позиции в игре.
Описана начальная позиция.
Ход игры
состоит в том, что один из игроков изменяет позицию.
Игроки ходят, чередуясь: Первый, Второй, Первый…
Партия заканчивается, когда возникла одна из заключительных позиций:
Партию выиграл Первый.
Партию выиграл Второй.
Партия закончилась вничью.
Игроки ходят, чередуясь: Первый, Второй, Первый…
Партия заканчивается, когда возникла одна из заключительных позиций:
Партию выиграл Первый.
Партию выиграл Второй.
Партия закончилась вничью.
Слайд 8Дано:
Игроков – 2.
2 кучи камней: в 1-ой 3 камня, во 2-ой
2 камня.
Условие: У каждого игрока неограниченно много камней. За один ход каждый игрок может доложить в одну из кучь или 1 камень, или утроить их число.
Требуется :
Сумма камней в обеих кучах должна стать не менее 16.
Условие: У каждого игрока неограниченно много камней. За один ход каждый игрок может доложить в одну из кучь или 1 камень, или утроить их число.
Требуется :
Сумма камней в обеих кучах должна стать не менее 16.
Задача
+1
*3
Слайд 9 Выигрышная
стратегия
* достаточно использовать метод перебора всех возможных вариантов ходов игроков;
*применить метод построения деревьев;
*если от каждого узла дерева отходят две ветви, т.е. возможные варианты хода, то такое дерево называется двоичным (если из каждой позиции есть три варианта продолжения, дерево будет троичным и т.д.).
Слайд 10Выигрышные и проигрышные позиции.
выигрышная позиция – это такая позиция, в которой игрок,
делающий первый ход, обязательно выиграет при любых действиях соперника, если не допустит ошибки; при этом говорят, что у данного игрока есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть;
если игрок, делающий первый ход, находится в проигрышной позиции, то он обязательно проиграет, если ошибку не сделает его оппонент; в этом случае говорят, что у данного игрока нет выигрышной стратегии.
Общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для оппонента.
если игрок, делающий первый ход, находится в проигрышной позиции, то он обязательно проиграет, если ошибку не сделает его оппонент; в этом случае говорят, что у данного игрока нет выигрышной стратегии.
Общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для оппонента.
Слайд 13Победа первого игрока:
(3,2) – (4,2) – (5,2) – (15,2)
(3,2) – (4,2)
– (12,2) – (12,6)
(3,2) – (4,2) – (4,6) – (4,18)
(3,2) - (3,3) – (3,9) – (9,9)
(3,2) – (4,2) – (4,6) – (4,18)
(3,2) - (3,3) – (3,9) – (9,9)
Победа второго игрока:
(3,2) – (4,2) – (4,3) - (5,3) – (15,3)
(3,2) – (4,2) – (4,3) – (12,3) – (12,9)
(3,2) – (4,2) – (4,3) – (4,4) – (12,4)
(3,2) – (4,2) – (4,3) – (4,12) – (5,12)
(3,2) - (9,2) - (27,2)
(3,2) - (3,3) - ( 3,4) – (4,4) - (12,4)
(3,2) - (3,3) - ( 3,4) – (9,4) - (9,12)
(3,2) - (3,3) - ( 3,4) – (3,5) - (3,15)
(3,2) - (3,3) - ( 3,4) – (3,12) - (4,12)
(3,2) - (3,6) - ( 3,18)
Слайд 15 Задача «Поиск фальшивой монеты»
Дано: 12 монет. Одна из них фальшивая,
т.е. отличается массой, а именно легче других настоящих. Рычажные или чашечные весы без разновеса .
Требуется: Найти фальшивую монету за наименьшее число взвешиваний.
Требуется: Найти фальшивую монету за наименьшее число взвешиваний.
