края
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для дополнительных занятий по информатике Вычислительная геометрия
Содержание
- 1. Презентация для дополнительных занятий по информатике Вычислительная геометрия
- 2. Вычислительная геометрия — это раздел математики, изучающий
- 3. Векторное произведение векторов
- 4. Модуль векторного произведенияравен площади параллелограмма илиудвоенной площади треугольника,построенного на перемножаемых векторах
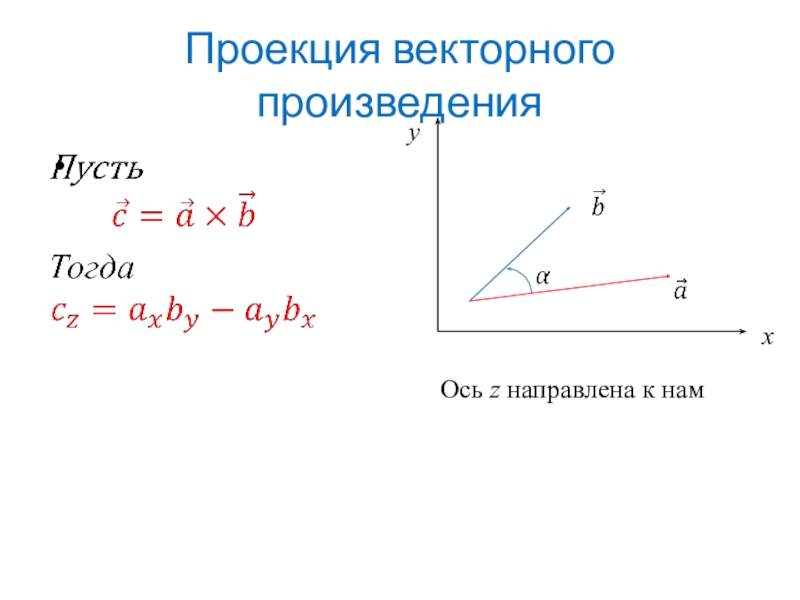
- 5. Проекция векторного произведенияОсь z направлена к нам
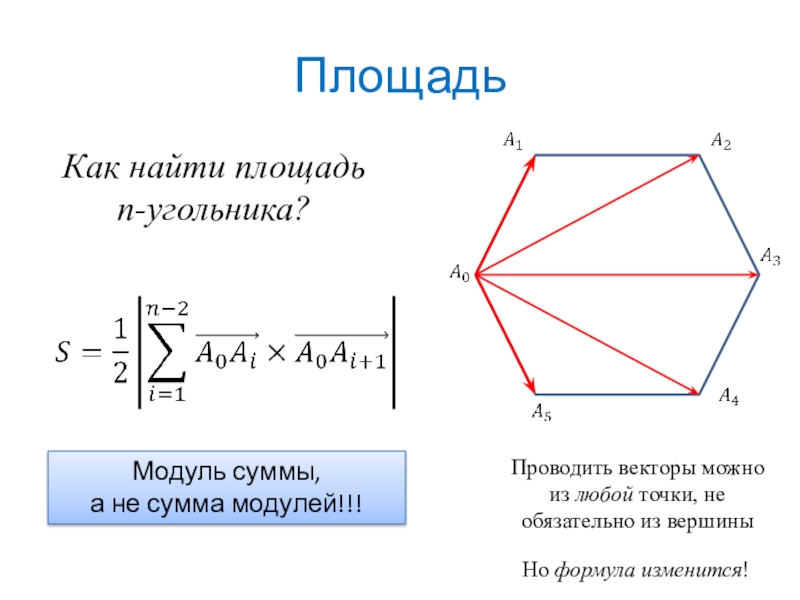
- 6. ПлощадьКак найти площадь n-угольника?Модуль суммы, а не
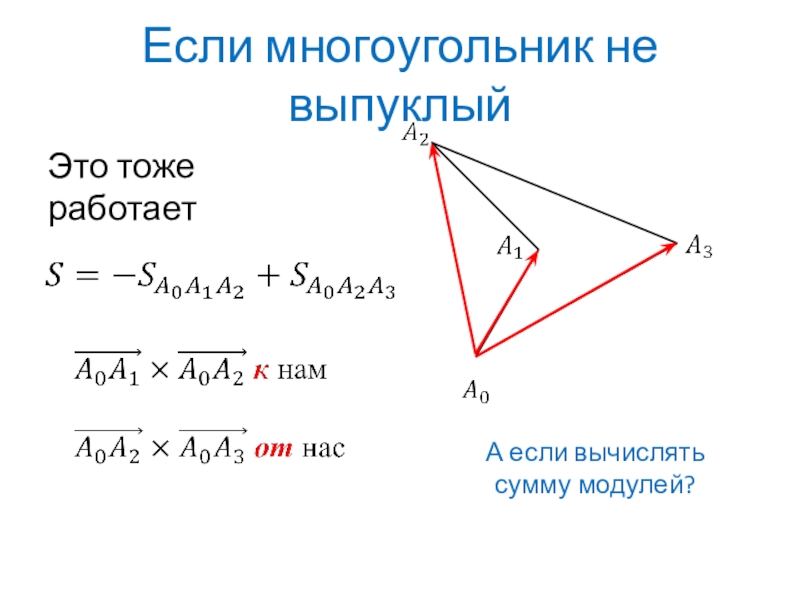
- 7. Если многоугольник не выпуклыйЭто тоже работаетА если вычислять сумму модулей?
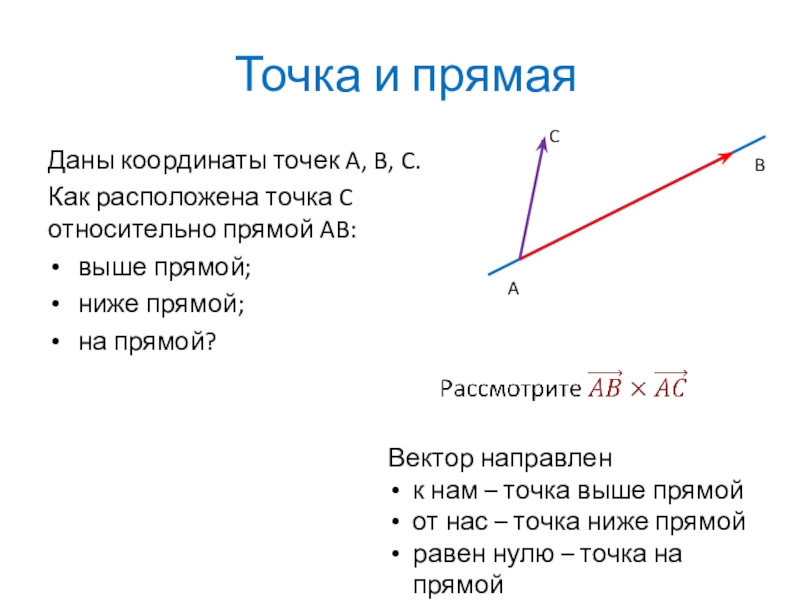
- 8. Точка и прямаяДаны координаты точек A, B,
- 9. Прямая и отрезокПересекает ли прямая AB отрезок
- 10. Два отрезкаПересекаются ли отрезки AB и CD?Ответ.
- 11. Направление обходаВ каком порядке: по часовой стрелке
- 12. Выпуклый?Заданы координаты вершин простого многоугольника в направлении
- 13. ЛитератураКормен Т., Лейзерсон Ч., Ривест Р., Штайн
Вычислительная геометрия — это раздел математики, изучающий алгоритмы решения геометрических задач.http://rain.ifmo.ru/cat/view.php/theory/math/geometry-2005 Вычислительная геометрия — это раздел теории вычислительных систем, изучающий алгоритмы, предназначенные для решения геометрических задач.Кормен и др.Что такое вычислительная геометрия?
Слайд 1Вычислительная геометрия
Середа Александр Николаевич,
учитель информатики
МОУ СОШ №25 ст-цы Должанской
МО Ейский район
Краснодарского
Слайд 2Вычислительная геометрия — это раздел математики, изучающий алгоритмы решения геометрических задач.
http://rain.ifmo.ru/cat/view.php/theory/math/geometry-2005
Вычислительная геометрия — это раздел теории вычислительных систем, изучающий алгоритмы, предназначенные для решения геометрических задач.
Кормен и др.
Что такое вычислительная геометрия?
Слайд 4Модуль векторного произведения
равен
площади параллелограмма или
удвоенной площади треугольника,
построенного на перемножаемых векторах
Слайд 6Площадь
Как найти площадь
n-угольника?
Модуль суммы,
а не сумма модулей!!!
Проводить векторы можно из любой
точки, не обязательно из вершины
Но формула изменится!
Слайд 8Точка и прямая
Даны координаты точек A, B, C.
Как расположена точка C
относительно прямой AB:
выше прямой;
ниже прямой;
на прямой?
выше прямой;
ниже прямой;
на прямой?
B
A
. C
Вектор направлен
к нам – точка выше прямой
от нас – точка ниже прямой
равен нулю – точка на прямой
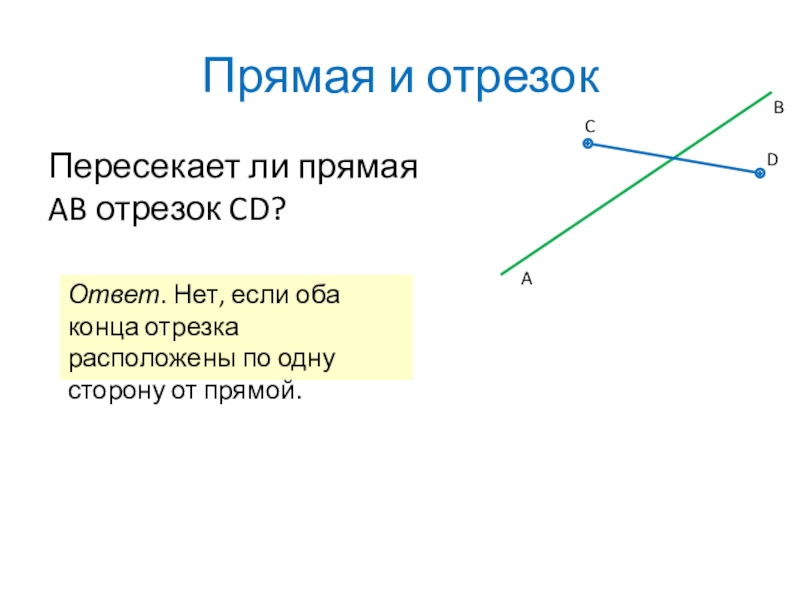
Слайд 9Прямая и отрезок
Пересекает ли прямая AB отрезок CD?
A
B
C
D
Ответ. Нет, если оба
конца отрезка расположены по одну сторону от прямой.
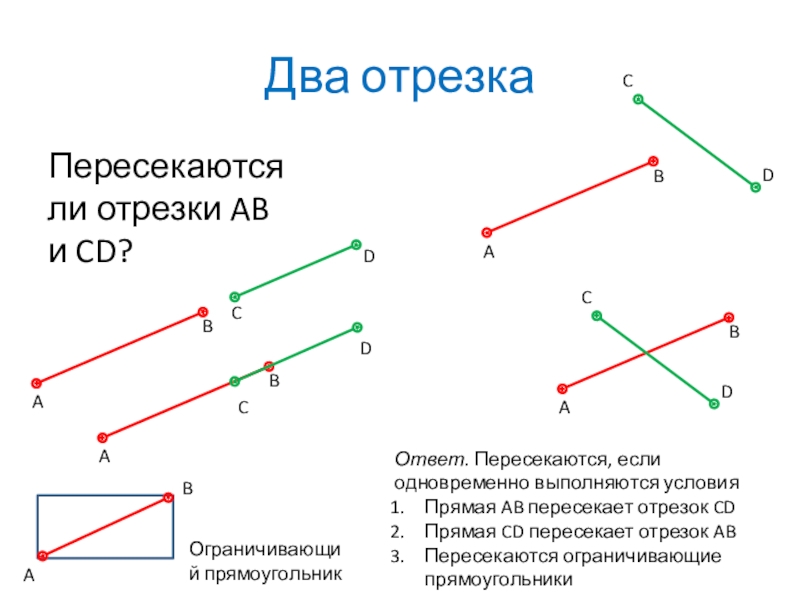
Слайд 10Два отрезка
Пересекаются ли отрезки AB и CD?
Ответ. Пересекаются, если одновременно выполняются
условия
Прямая AB пересекает отрезок CD
Прямая CD пересекает отрезок AB
Пересекаются ограничивающие прямоугольники
Прямая AB пересекает отрезок CD
Прямая CD пересекает отрезок AB
Пересекаются ограничивающие прямоугольники
A
B
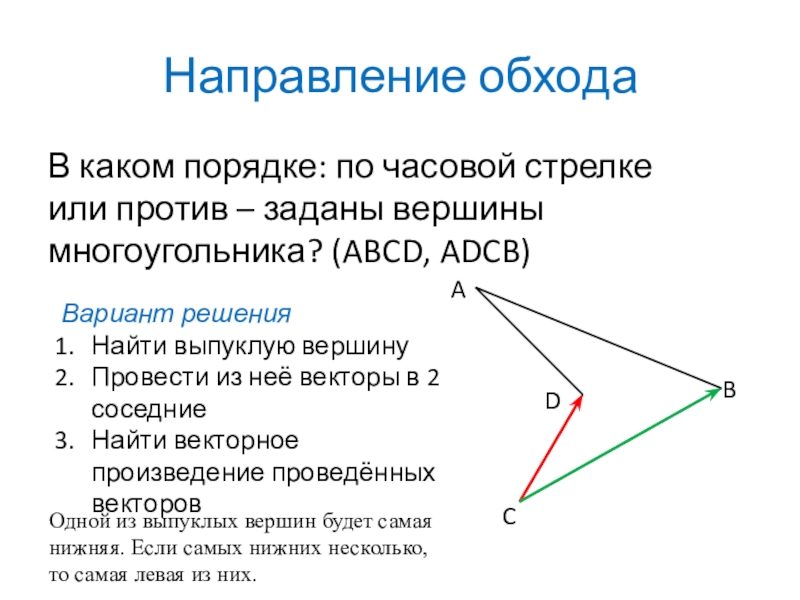
Слайд 11Направление обхода
В каком порядке: по часовой стрелке или против – заданы
вершины многоугольника? (ABCD, ADCB)
Вариант решения
Найти выпуклую вершину
Провести из неё векторы в 2 соседние
Найти векторное произведение проведённых векторов
Одной из выпуклых вершин будет самая нижняя. Если самых нижних несколько, то самая левая из них.
A
B
C
D
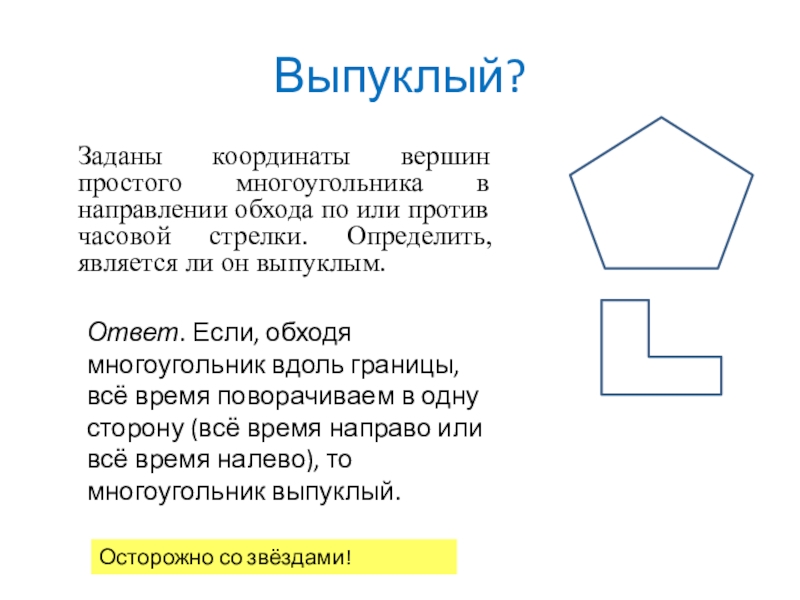
Слайд 12Выпуклый?
Заданы координаты вершин простого многоугольника в направлении обхода по или против
часовой стрелки. Определить, является ли он выпуклым.
Ответ. Если, обходя многоугольник вдоль границы, всё время поворачиваем в одну сторону (всё время направо или всё время налево), то многоугольник выпуклый.
Осторожно со звёздами!
Слайд 13Литература
Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и
анализ, 2-е издание. : Пер. с англ. — М.: Издательский дом «Вильямс», 2010
Вычислительная геометрия // Дискретная математика: алгоритмы: http://rain.ifmo.ru/cat/view.php/theory/math/geometry-2005.
Вычислительная геометрия // Дискретная математика: алгоритмы: http://rain.ifmo.ru/cat/view.php/theory/math/geometry-2005.
