- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Представление числовой информации в компьютере
Содержание
- 1. Представление числовой информации в компьютере
- 2. Тема урока Представление числовой
- 3. Цели и задачи урока: Образовательные:расширить представление
- 4. Какова информационная картина мира ребенка дошкольного возраста?Какова
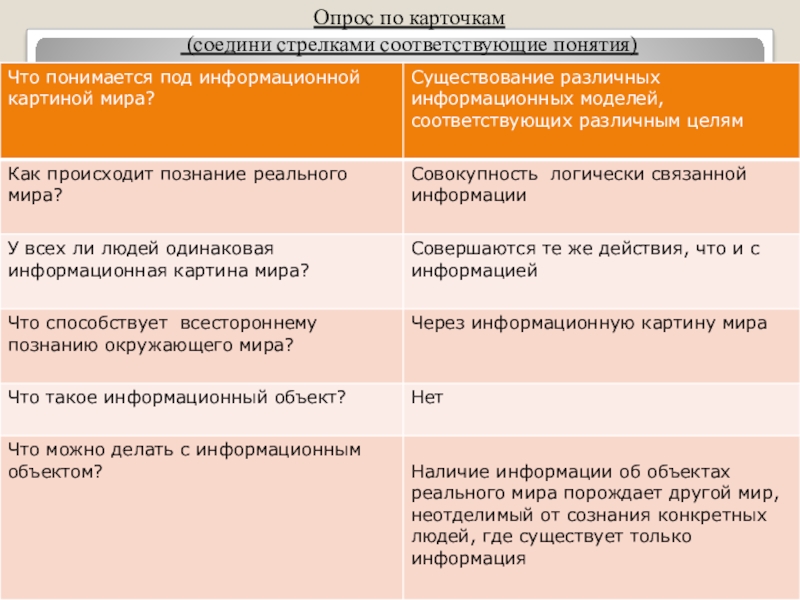
- 5. Опрос по карточкам (соедини стрелками соответствующие понятия)
- 6. Опрос по карточкам (соедини стрелками соответствующие понятия)
- 7. Взаимопроверка работоценка 5- нет ошибок;оценка 4
- 8. Тема урока: Представление числовой информации в компьютере
- 9. История развития систем счисления
- 10. Единичная (унарная) система счисления
- 11. Понятие «системы счисления»
- 12. Системы счисленияПозиционныеНепозиционные (записывают в тетради)
- 13. Непозиционные системы счисления: Непозиционная с.с.
- 14. Непозиционные системы счисления: Египетская нумерация1
- 15. Непозиционные системы счисления: Древнегреческая нумерация
- 16. Римская система счисления До
- 17. Непозиционные системы счисления имеют ряд существенных недостатков:
- 18. Позиционные системы счисления В таких
- 19. Основные достоинства любой позиционной системы счисления: ограниченное
- 20. В компьютере наиболее подходящей и надежной оказалась
- 21. Кроме того оказалось удобным использовать представление информации
- 22. Алфавит системы счисления –
- 23. Укажите, какие числа записаны с ошибками. Обоснуйте ответ1567 3005,234 185,7948 110221345,526112,0113 16,545 13АЕ,1F16
- 24. Развернутой формой числа называется
- 25. Запишите в развернутой форме числа485,2310 = (решение
- 26. Перевод чисел из недесятичной позиционной системы счисления
- 27. Рассмотрим еще один пример. Переведем число 5D8,A16
- 28. Д/з §1.5, стр. 38-40Письменно№5, стр. 48, №6 стр.49
Слайд 1Пьер Симон Лаплас
(1749 – 1827 гг.)
«Мысль – выражать все числа
Слайд 2
Тема урока
Представление числовой информации в компьютере
Изучив эту тему вы узнаете:
система счисления;
непозиционные
позиционные системы счисления;
основание системы;
развернутая форма записи числа;
перевод чисел, представленных в различных позиционных системах счисления, в десятичную систему счисления.
Слайд 3Цели и задачи урока:
Образовательные:
расширить представление о различных системах счисления;
научить
Воспитательные:
воспитывать активность и сознательность детей;
умение контролировать и оценивать свою деятельность.
Развивающие:
развивать коммуникативные навыки;
развивать кругозор, внимание.
Слайд 4Какова информационная картина мира ребенка дошкольного возраста?
Какова информационная картина мира старшеклассника?
Какова
Опрос по карточкам
Слайд 7Взаимопроверка работ
оценка 5- нет ошибок;
оценка 4 – 1, 2 ошибки;
оценка
оценка 2 – более 3 ошибок.
Слайд 10Единичная (унарная) система счисления
Примеры:
зарубки
черточки
палочки
По курсам обучения курсантов
5 курс 4 курс 3 курс 2 курс 1 курс
Слайд 11Понятие «системы счисления»
(записывают в тетради)
Система счисления – это совокупность правил записи чисел с помощью определённого набора символов
Слайд 13Непозиционные
системы счисления:
Непозиционная с.с. – это система счисления,
(записывают в тетради)
Слайд 14Непозиционные системы счисления:
Египетская нумерация
1 10
10000 100000 1000000 10000000
Возникла 5000 лет тому назад
В V веке до н.э. появилась алфавитная нумерация.
Слайд 16Римская система счисления
До нас дошла римская система
VI = 6, т.е. 5 + 1,
LX = 60, т.е. 50 + 10,
IV = 4, т.е. 5 – 1,
XL = 40, т е. 50 – 10.
Цифры записываются слева направо в порядке убывания. Их значения складываются. Если слева стоит меньшая цифра, а справа – большая, то их значения вычитаются
Слайд 17Непозиционные системы счисления имеют ряд существенных недостатков:
Какие?
Существует постоянная потребность введения
Невозможно представлять дробные и отрицательные числа.
Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.
Слайд 18Позиционные системы счисления
В таких системах счисления, в отличие
на каком месте в записи числа стоит цифра, зависит та величина, которую она обозначает.
Например, меняя позицию цифры 2 в десятичной системе счисления, можно записать разные по величине десятичные числа: 2; 20; 2000; 0,02 и т.д.
Основание системы счисления – количество (p) различных символов, используемых для изображения числа в позиционной системе счисления
(работа с учебником стр. 38-39 читают ученики)
Слайд 19Основные достоинства любой позиционной системы счисления:
ограниченное количество символов для записи чисел;
простота
Например: в арабской десятичной системе счисления для записи чисел используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего таких цифр – 10, т.е 10 – основание арабской системы счисления. Поэтому ее и называют десятичной системой счисления.
Слайд 20В компьютере наиболее подходящей и надежной оказалась двоичная система счисления ,
Однако эта система счисления была предметом пристального внимания. Вот, что писал выдающийся французский математик Пьер Симон Лаплас (1749 - 1807) об отношении к двоичной системе счисления:
«В своей двоичной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль – небытиё, и что высшее существо создаёт все сущее из небытия точно таким же образом, как единица и нуль в его системе выражают все числа».
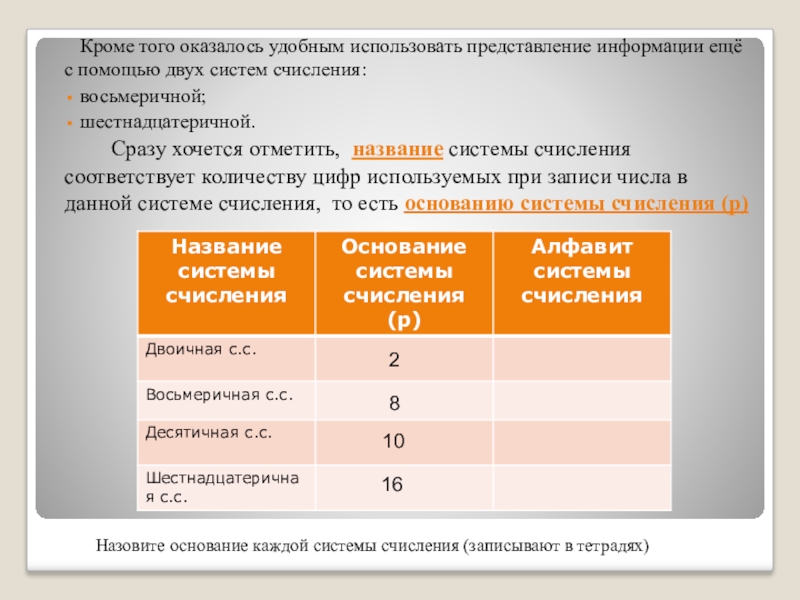
Слайд 21Кроме того оказалось удобным использовать представление информации ещё с помощью двух
восьмеричной;
шестнадцатеричной.
Сразу хочется отметить, название системы счисления соответствует количеству цифр используемых при записи числа в данной системе счисления, то есть основанию системы счисления (р)
Назовите основание каждой системы счисления (записывают в тетрадях)
2
8
10
16
Слайд 22 Алфавит системы счисления – это набор символов,
(работа с учебником стр. 39 читают ученики)
Хочется отметить, что используются цифры от 0 до р-1, где р – основание системы счисления)
Исходя из это заполним таблицу
0,1
0,1,2,3,4,5,6,7
0,1,2,3,4.5,6,7,8,9
0,1,2,3,4.5,6,7,8,9,10(A),11(B),12(C),13(D),14(E),15(F)
Назовите алфавит каждой системы счисления (записывают в тетрадях)
Слайд 23Укажите, какие числа записаны с ошибками. Обоснуйте ответ
1567
3005,234
185,7948
11022
1345,526
112,0113
16,545
13АЕ,1F16
Слайд 24
Развернутой формой числа называется запись в виде:
Nр=ak*рk+ak-1*рk-1+…+a1*р1 +a0*р0+a-1*р-1+ …+a-n*р-n
Любое действительное число
системе счисления в виде суммы положительных и отрицательных
степеней числа р (основание системы счисления)
N - само число
р – основание системы счисления
к+1 – количество разрядов в целой части числа
n - количество разрядов в дробной части числа
Слайд 25Запишите в развернутой форме числа
485,2310 = (решение на доске)
123,4510 =
(решает ученик
11011,1012 = (решение на доске)
4. 111011,112 =
2 1 0 -1 -2
1 *102+2*101+3*100+4*10-1+5*10-2
5 4 3 2 1 0 -1 -2
1 *25+1*24+1*23+1*21+1*20 +1*2-1+1*2-2
(4, 5, 6 записывают решение на доске ученики)
5. 3456,68 =
3 2 1 0 -1
3 *83+4*82+5*81+6*80+6*8-1
6. 3AF,1516 =
2 1 0 -1 -2
3 *162+10*161+15*160+1*16-1+5*16-2
Слайд 26Перевод чисел из недесятичной позиционной системы счисления в десятичную
Чтобы перевести число
Например, переведем число 1011,112 в десятичную систему счисления. Для этого представим это число в развернутой форме и произведем вычисления в десятичной системе счисления.
Рассмотрим еще один пример. Переведем число 51,78 в десятичную систему счисления.
3 2 1 0 -1-2
1 0 -1
Слайд 27Рассмотрим еще один пример. Переведем число 5D8,A16 в десятичную систему счисления.
5D,A16
Мы перевели три числа из недесятичной системы счисления в десятичную. Можем ли мы их теперь расположить в порядке возрастания?
5D,A16, ,
5D,A16
1 0 -1
Вывод: (делают ученики)
Чтобы сравнить числа записанные в разных системах счисления, надо их представить в одной системе счисления (желательно в десятичной)