- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Представление чисел в памяти компьютера
Содержание
- 1. Представление чисел в памяти компьютера
- 2. "Все есть число", — говорили пифагорийцы, подчеркивая необычайно важную роль чисел в практической деятельности.
- 3. Цель урока: знакомство с представлением чисел в
- 4. Главное- видеть цель,а дорога к ней всегда
- 5. Актуализация знаний.Что такое системы счисления? Назовите распространенные
- 6. Система счисления (СС) – знаковая система, в
- 7. Слайд 7
- 8. Непозиционная система счисления - система, в которой
- 9. Непозиционная система счисления. В непозиционной системе
- 10. Позиционная система счисления. Система счисления называется позиционной, если
- 11. В любой позиционной системе число может быть
- 12. Основание системы – количество цифр в её алфавите.A=10, B=11, C=12, D=13, E=14, F=15
- 13. Самостоятельная работа Вариант 1Перевести число в двоичную
- 14. Информация в компьютере представлена в двоичном коде, алфавит которого состоит из двух цифр (0 и 1)
- 15. n - 1 разряд0 разрядЯчейка – это
- 16. n - 1 разряд0 разрядСодержимое ячейки памяти
- 17. Нумерацию разрядов в ячейке принято вести
- 18. Единицы измерения объема информацииКоличество информации, хранящейся в
- 19. 8 бит = 1 байтБайт - основная
- 20. Форматы данных. . .0708 715008 78 716
- 21. Единицы измерения объема информации1 Килобайт (Кбайт) =
- 22. Слайд 22
- 23. Представление целого числа Разрядная сетка: восемь разрядов
- 24. Беззнаковый целый типМинимальное число:Максимальное число:111111112= =1*27 +
- 25. Алгоритм представления в компьютере целых положительных чисел:k = 16 разрядов54 =1101102k = 8 разрядов
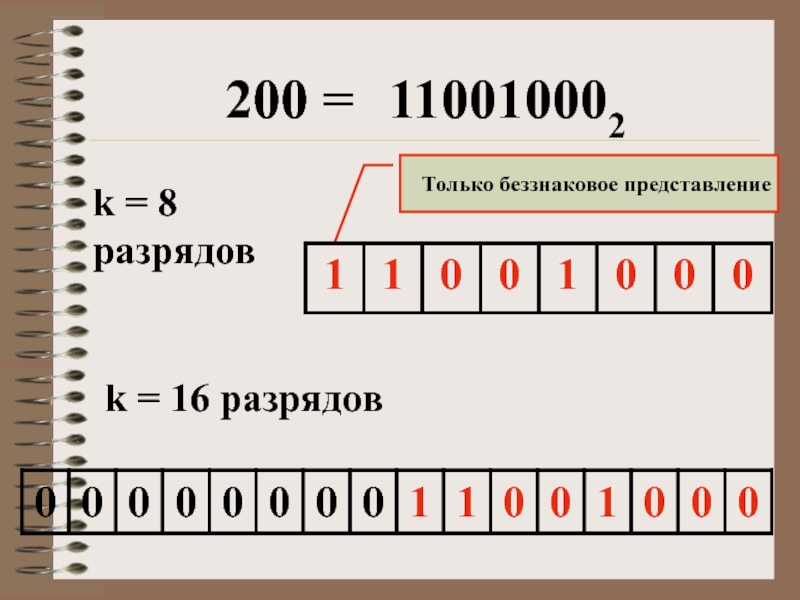
- 26. k = 16 разрядовТолько беззнаковое представление200 =110010002k = 8 разрядов
- 27. В ЭВМ в целях упрощения выполнения арифметических
- 28. Разряды числа в коде жестко связаны с
- 29. Прямой код двоичного числа совпадает по изображению
- 30. Обратный код для положительного числа совпадает с
- 31. Дополнительный код для положительного числа совпадает с прямым кодом.Дополнительный код двоичного числа+1101
- 32. Для отрицательного числа дополнительный код образуется путем
- 33. Получить дополнительный код числа для 8-разрядной ячейки.Однобайтовое представление числа:-117
- 34. Получить дополнительный код числа для 16-разрядной ячейки.Двухбайтовое представление числа:-117
- 35. Получить дополнительный код двоичного числа для 8-разрядной ячейки.-10002
- 36. Все целые отрицательные числа в компьютере представляются дополнительным кодом.
- 37. ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛЧасть памяти, в которой хранится
- 38. ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛКак разместить число -25?
- 39. Слайд 39
- 40. Число 3910 = 100111 2 в однобайтовом
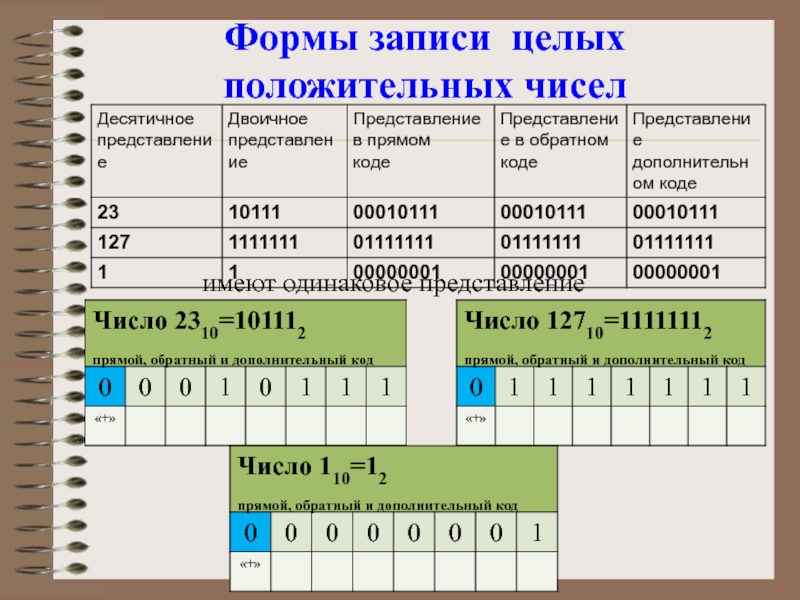
- 41. Формы записи целых положительных чиселимеют одинаковое представление
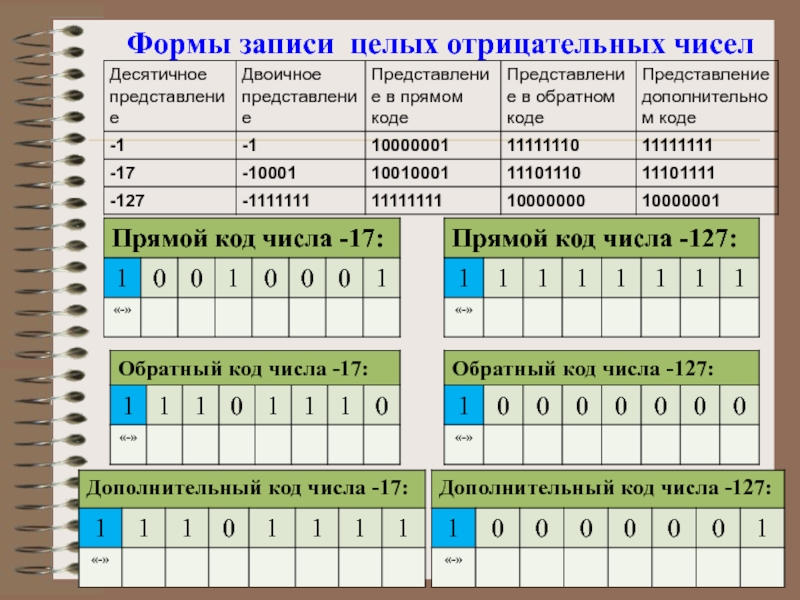
- 42. Формы записи целых отрицательных чисел
- 43. Физкультминутка
- 44. В какой из последовательностей единицы измерения информации
- 45. 2. Один байт равен:16 битам;8 битам;32 битам;2 битам.
- 46. Количество разрядов занимаемых двухбайтовым числом равно:а) 8;б) 16;в) 32;г) 64.
- 47. Отрицательный знак числа в разрядной сетке обозначается:0;1;-;+.
- 48. Количество разрядов занимаемых однобайтовым числом равно:а) 8;б) 16;в) 32;г) 64.
- 49. Дополнительный код отрицательного числа образуется: а) инвертированием
- 50. 7.Наибольшую последовательность битов, обрабатываемую компьютером как единое целое, называют:машинным порядком;байтом;машинным словом;адресом.
- 51. 8. Получить внутреннее представление целого числа 34 в 8-разрядной ячейке памяти компьютера..
- 52. 9. Получить внутреннее представление целого числа -34 в 8-разрядной ячейке памяти компьютера..
- 53. 10. Получить внутреннее представление целого числа 123 в 8-разрядной ячейке памяти компьютера..
- 54. 11. Получить внутреннее представление целого числа -123 в 8-разрядной ячейке памяти компьютера..
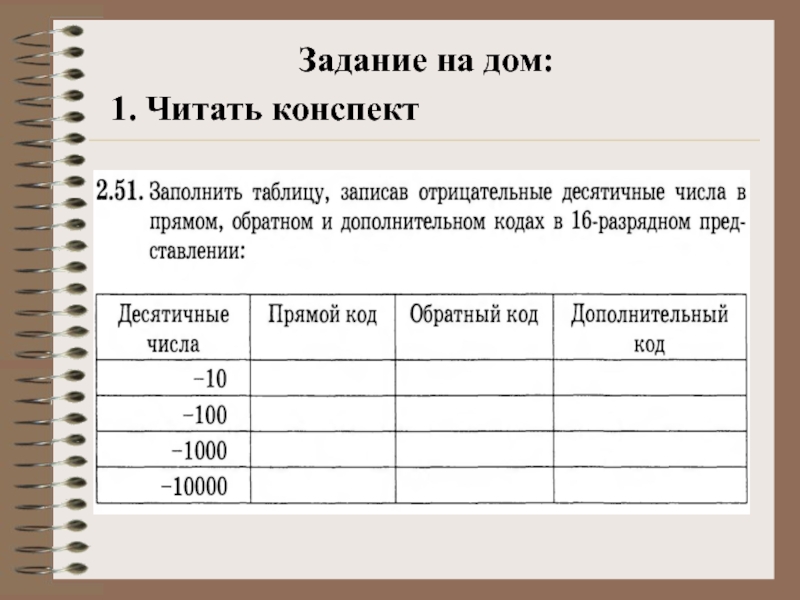
- 55. Задание на дом: 1. Читать конспект
- 56. Слайд 56
- 57. Слайд 57
Слайд 2"Все есть число", — говорили пифагорийцы, подчеркивая необычайно важную роль чисел
Слайд 3Цель урока: знакомство с представлением чисел в памяти компьютера.
Задачи урока:
Образовательная –
Воспитательная – воспитание информационной культуры учащихся, внимательности, аккуратности, дисциплинированности, усидчивости, привитие навыков самостоятельной работы, обеспечение сознательного усвоения учебного материала.
Развивающая – развивать алгоритмическое мышление, познавательный интерес, прививать исследовательские навыки.
Слайд 4Главное- видеть цель,
а дорога к ней всегда найдется.
- Ребята, сегодня перед
Мотивация урока.
Слайд 5Актуализация знаний.
Что такое системы счисления? Назовите распространенные системы счисления.
Что такое основание
Какой имеет алфавит и основание двоичная система счисления? Восьмеричная? Десятичная? Шестнадцатеричная?
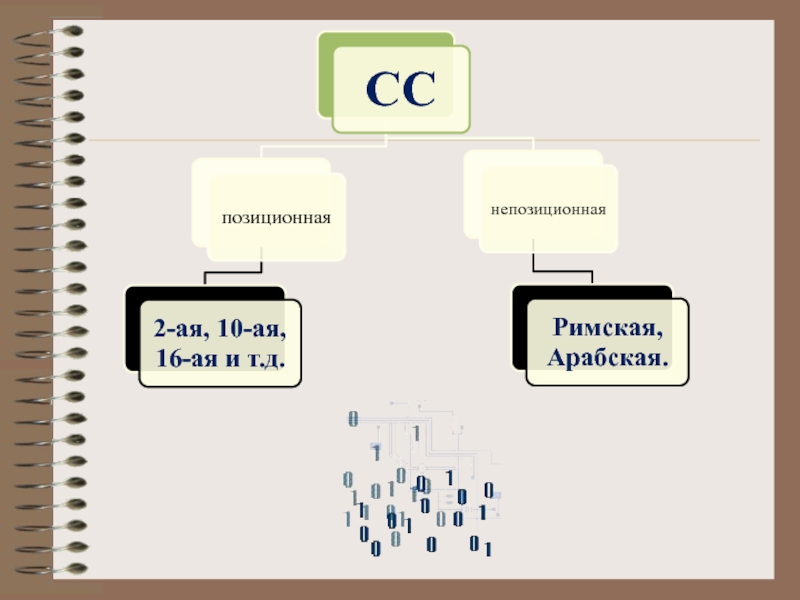
Слайд 6Система счисления (СС) – знаковая система, в которой числа записываются по
Слайд 8Непозиционная система счисления - система, в которой символы, обозначающие то или иное
Римские цифры
Древнерусский алфавит
Слайд 9Непозиционная система счисления.
В непозиционной системе счисления ВЕЛИЧИНА, ОБОЗНАЧАЕМАЯ В
Римская система счисления содержит 7 знаков для обозначения чисел. В качестве цифр используются некоторые буквы. I(1), V(5), X(10), L(50), C(100), D(500), M(1000). Значение цифры не зависит от ее положения в числе. Величина числа в римской системе счисления определяется как сумма или разность чисел. Десятичное число 28 представляется следующим образом:
XXVIII=10+10+5+1+1+1 (два десятка, пяток, три единицы).
Десятичное число 99 имеет следующее представление:
XCIХ = –10+100–1+10.
9 = IX, 158 = CLYIII, 1949 =MCMILIX
Слайд 10Позиционная система счисления.
Система счисления называется позиционной, если значение каждой цифры (ее
Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число — два, три, четыре, шестнадцать и т.д.
Слайд 11В любой позиционной системе число может быть представлено в виде многочлена.
4567 = 4000 + 500 + 60 + 7 =
4*103 + 5*102 + 6*101 + 7*100
Слайд 13Самостоятельная работа
Вариант 1
Перевести число в двоичную систему счисления: 3410
Перевести
Вариант 2
Перевести число в двоичную систему счисления: 2710
Перевести число из двоичной системы счисления в десятичную: 1101002
Слайд 14Информация в компьютере представлена в двоичном коде, алфавит которого состоит из
Слайд 15n - 1 разряд
0 разряд
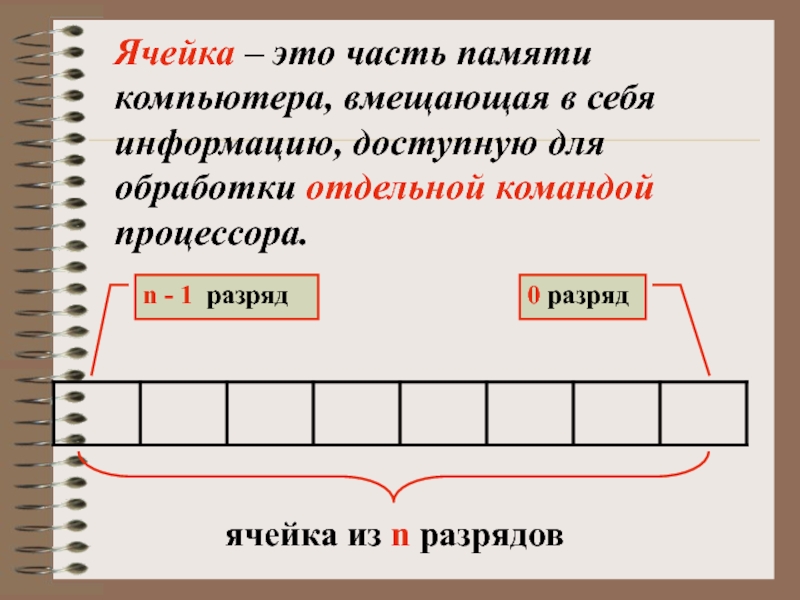
Ячейка – это часть памяти компьютера, вмещающая
Слайд 16n - 1 разряд
0 разряд
Содержимое ячейки памяти называется машинным словом.
Ячейка памяти
Слайд 17 Нумерацию разрядов в ячейке принято вести справа налево, самый правый
Содержимым любого разряда может быть либо 0, либо 1.
n - 1 разряд
0 разряд
Слайд 18Единицы измерения объема информации
Количество информации, хранящейся в ЭВМ, измеряется ее «объемом»,
Битом также называют
разряд ячейки памяти ЭВМ.
Слайд 198 бит = 1 байт
Байт - основная единица представления данных.
Байт (от
ячейка из 8 разрядов
7 разряд
0 разряд
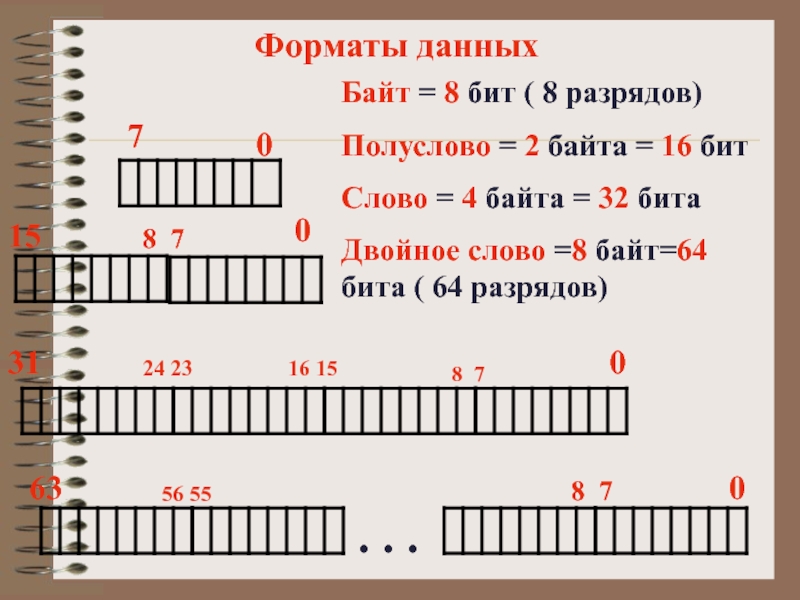
Слайд 20Форматы данных
. . .
0
7
0
8 7
15
0
0
8 7
8 7
16 15
24 23
31
63
56 55
Байт =
Полуслово = 2 байта = 16 бит
Слово = 4 байта = 32 бита
Двойное слово =8 байт=64 бита ( 64 разрядов)
Слайд 21Единицы измерения объема информации
1 Килобайт (Кбайт) = 1024 байт = 210
1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт;
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт;
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт;
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.
Слайд 23Представление целого числа
Разрядная сетка:
восемь разрядов (1 байт);
шестнадцать разрядов
тридцать два разряда (4 байта);
Беззнаковый целый тип
Знаковый целый тип
Слайд 24Беззнаковый целый тип
Минимальное число:
Максимальное число:
111111112=
=1*27 + 1*26 + 1*25 + 1*24
в байте (8 разрядов) можно представить
беззнаковые числа от 0 до 255.
Слайд 25Алгоритм представления в компьютере целых положительных чисел:
k = 16 разрядов
54 =
1101102
k
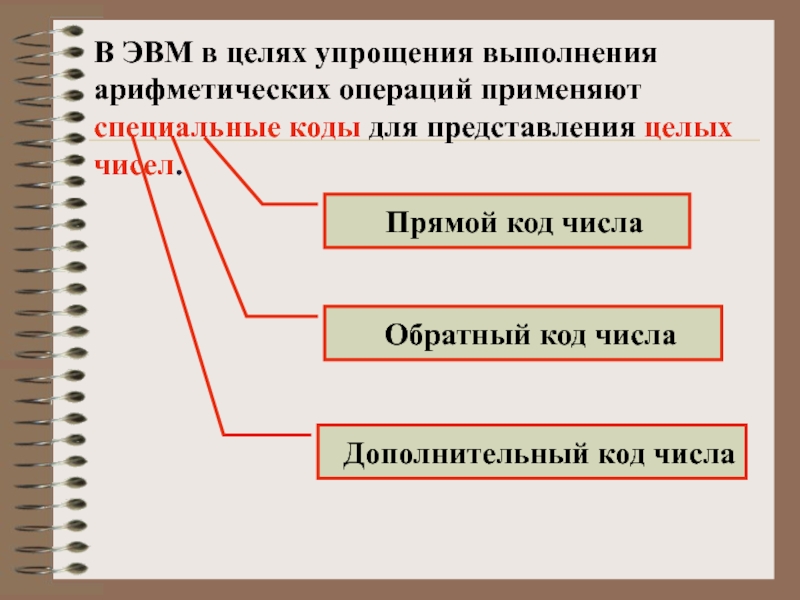
Слайд 27В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для
Прямой код числа
Обратный код числа
Дополнительный код числа
Слайд 28Разряды числа в коде жестко связаны с разрядной сеткой (8, 16,
Для записи кода знака числа в разрядной сетке отводится фиксированный разряд.
Знаковым разрядом является старший разряд в разрядной сетке.
знаковый разряд
0
7
0
Слайд 29Прямой код двоичного числа совпадает по изображению с записью самого числа.
Значение
Прямой код двоичного числа
+1101
-1101
1
Слайд 30Обратный код для положительного числа совпадает с прямым кодом.
Для отрицательного числа
Обратный код двоичного числа
+1101
-1101
- прямой код
- обратный код
- прямой код
- обратный код
Слайд 31Дополнительный код для положительного числа совпадает с прямым кодом.
Дополнительный код двоичного
+1101
Слайд 32Для отрицательного числа дополнительный код образуется путем получения обратного кода и
Дополнительный код двоичного числа
-1101
Слайд 33Получить дополнительный код числа
для 8-разрядной ячейки.
Однобайтовое представление числа:
-117
Слайд 34Получить дополнительный код числа
для 16-разрядной ячейки.
Двухбайтовое представление числа:
-117
Слайд 37ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ
Часть памяти, в которой хранится число называют ячейкой, минимальный
Как поместить туда число (например 25)? Переведём его в двоичную систему → 11001 хранит знак числа ( + обозначается 0, - обозначается 1) максимальное положительное число - 127
1
0
0
1
1
1
0
1
0
0
Слайд 38ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
Как разместить число -25?
Для размещения отрицательных чисел используется
Алгоритм получения дополнительного кода: а) записать внутреннее представление соответствующего положительного числа → 00011001 б) записать обратный код полученного числа заменой во всех разрядах 0 на 1 и 1 на 0 → 11100110 в) к полученному числу прибавить 1 → 11100111 В результате выполнения такого алгоритма единица получается автоматически.
1
1
1
1
0
1
1
0
1
1
Слайд 40Число 3910 = 100111 2 в однобайтовом формате:
Число 3910 = 100111
Число 65 53510 = 11111111 111111112 в двубайтовом формате:
Слайд 44В какой из последовательностей единицы измерения информации указаны в порядке возрастания:
байт,
килобайт, байт, бит, мегабайт;
байт, мегабайт, килобайт, гигабайт;
мегабайт, килобайт, гигабайт, байт;
байт, килобайт, мегабайт, гигабайт?
Самостоятельная работа по теме.
Слайд 49
Дополнительный код отрицательного числа образуется:
а) инвертированием разрядов числа;
б) прибавлением единицы
в) вычитанием единицы из младшего разряда обратного кода числа;
г) прибавлением единицы к прямому коду числа.