- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение правильных многоугольников с помощью системы компьютерного черчения КОМПАС.
Содержание
- 1. Построение правильных многоугольников с помощью системы компьютерного черчения КОМПАС.
- 2. Цель работы: Изучить различные способы построения правильных
- 3. Теорема Гаусса — Ванцеляправильный n - угольник возможно построить
- 4. Задача. В данную окружность вписать правильный пятнадцатиугольник.
- 5. Задача. Построить правильный семнадцатиугольник.Строим окружность (O, OA).Проводим
- 6. Построение правильного девятиугольникаСпособ приближённого построения был
- 7. Теорема Мора — Маскерони Все построения, выполненные с помощь циркуля
- 8. Задача. Построить отрезок, четвёртый пропорциональный к трем
- 9. Доказательствo:∆AOA1 = ∆ BOB1 (no трем сторонам),
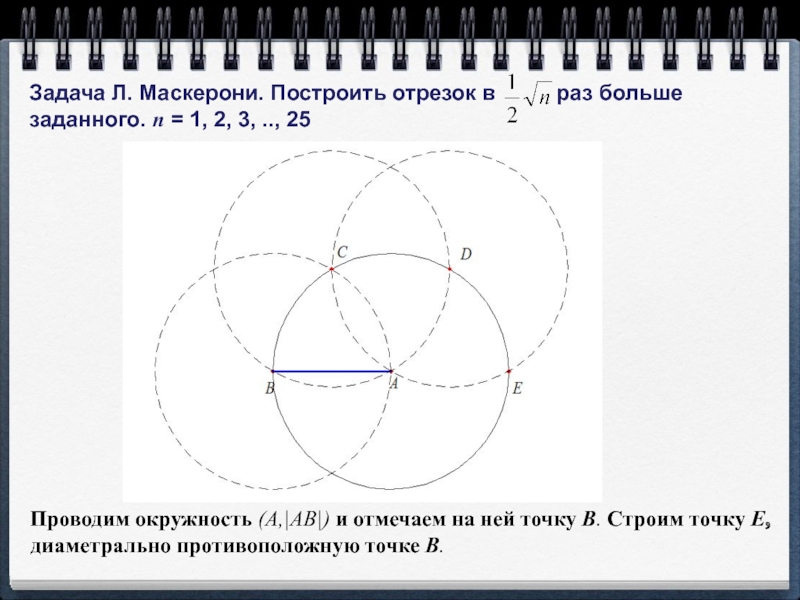
- 10. Задача Л. Маскерони. Построить отрезок в
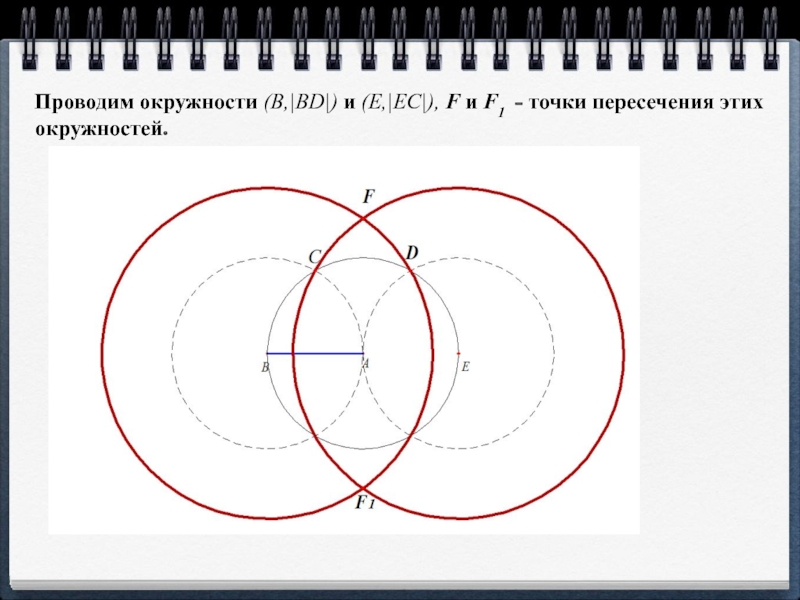
- 11. Проводим окружности (B,|BD|) и (E,|EC|), F и F1 - точки пересечения этих окружностей.
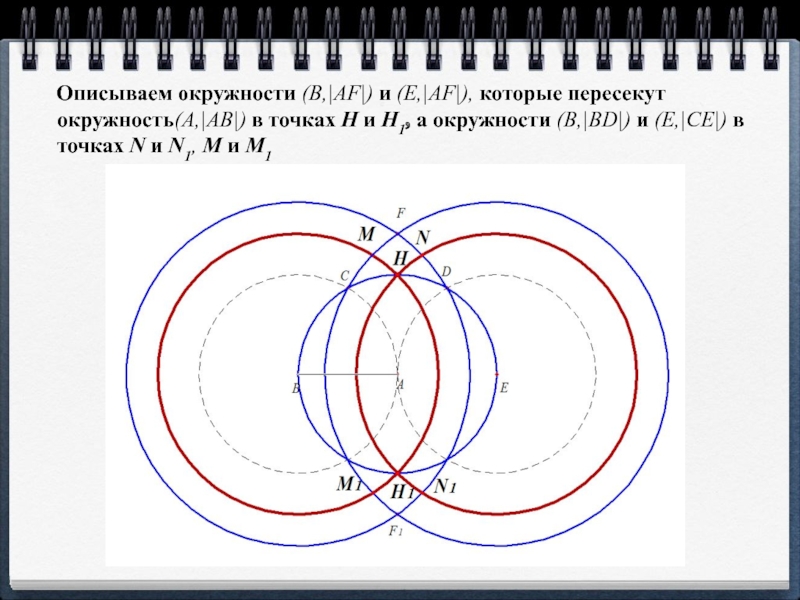
- 12. Описываем окружности (B,|AF|) и (E,|AF|), которые пересекут
- 13. Отмечаем точки P, P1, Q, Q1 пересечения окружностей (E,|AE|) и (B,|AB|) с окружностями (B,|AF|) и (E,|AF|)
- 14. Окружности (P,|BP|) и (P1,|BP1|) пересекутся в точке
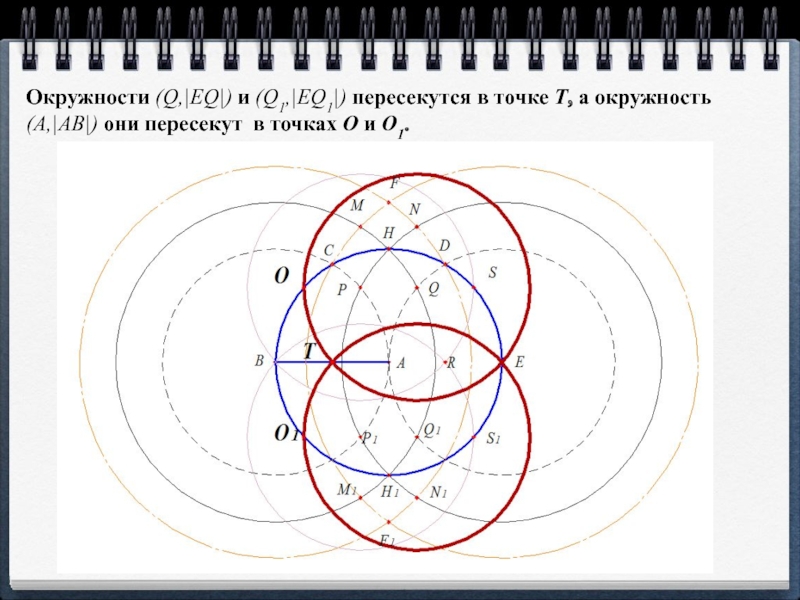
- 15. Окружности (Q,|EQ|) и (Q1,|EQ1|) пересекутся в точке
- 16. Проводим окружности (R,|AB|) и (F1,|AB|) и отмечаем точки L, L1, G пересечения их с окружностью (A,|AB|)
- 17. Описывает окружности (O,|AO|) и (O1,|AO1|), которые пересекутся в точке K
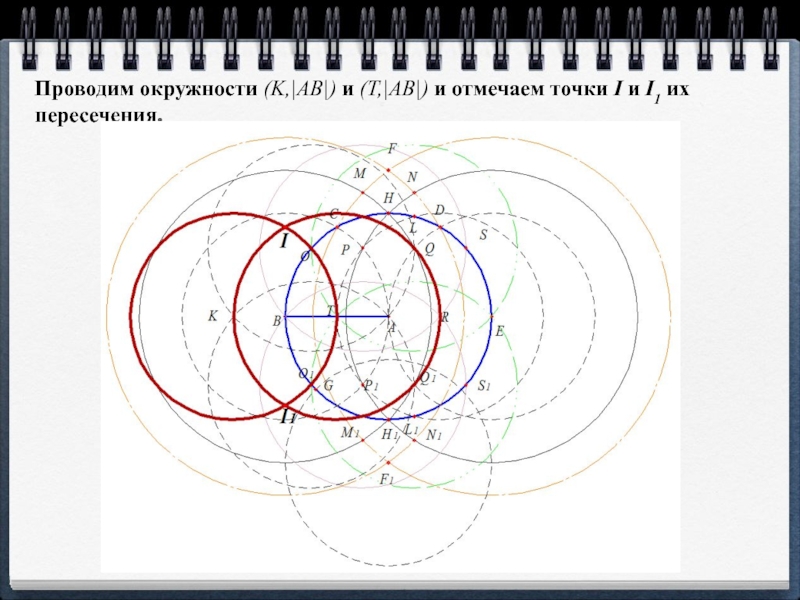
- 18. Проводим окружности (K,|AB|) и (T,|AB|) и отмечаем точки I и I1 их пересечения.
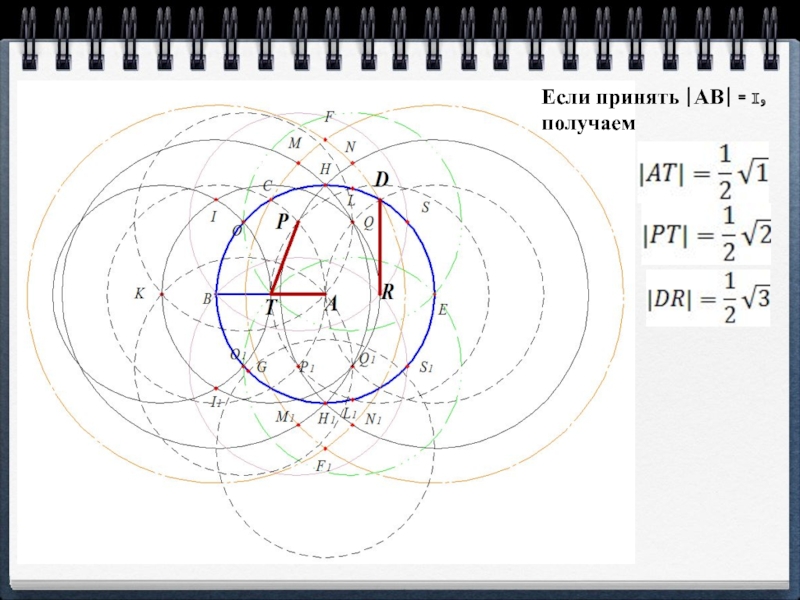
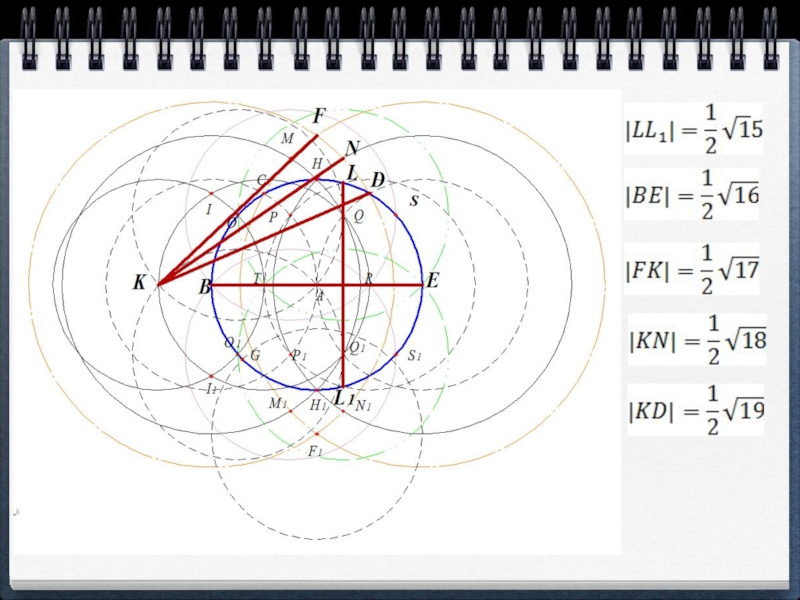
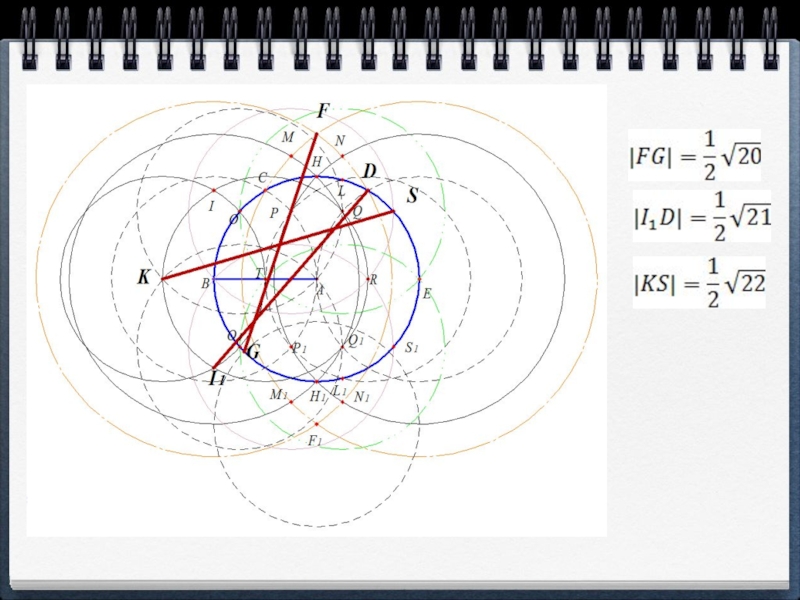
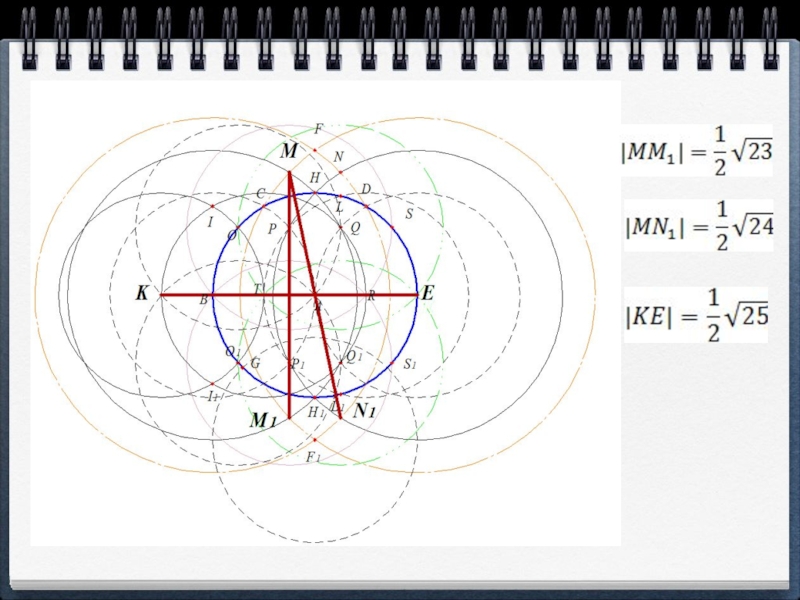
- 19. Если принять |АВ| = 1, получаем
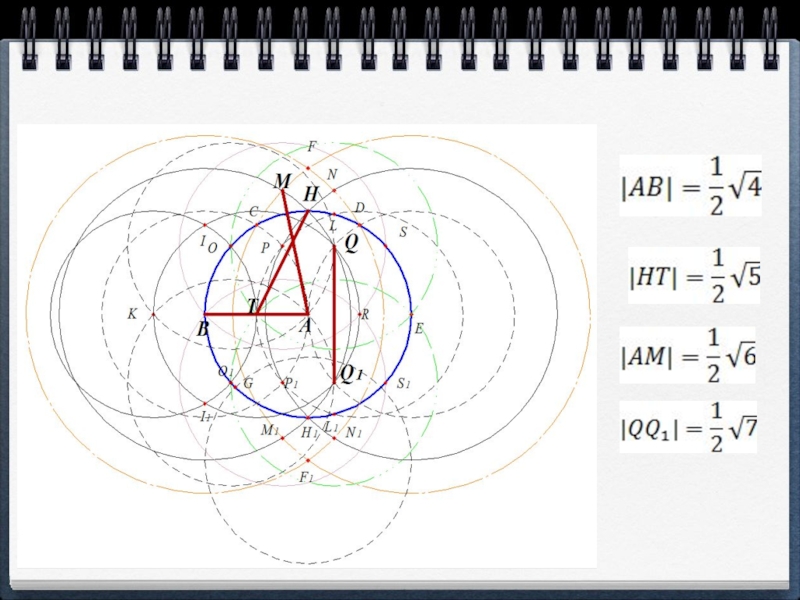
- 20. Слайд 20
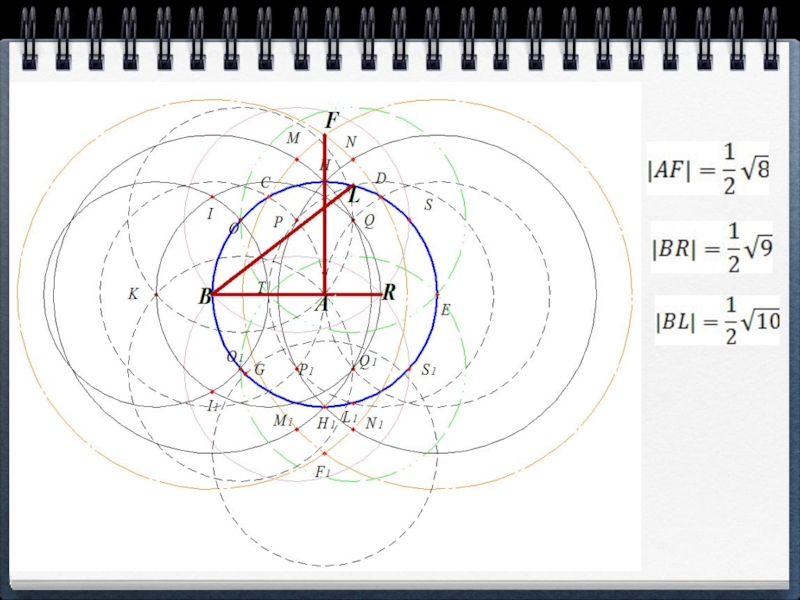
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
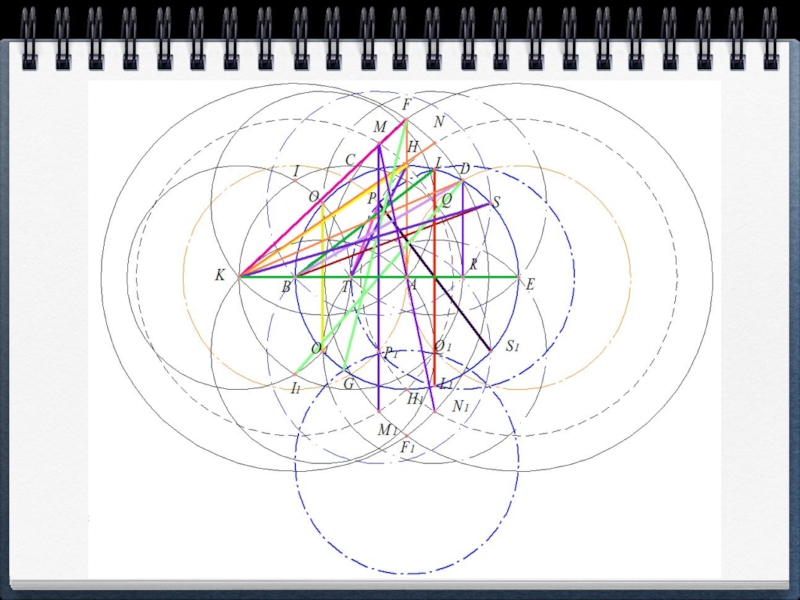
- 26.
- 27. Вывод В работе рассмотрен раздел геометрии – геометрия
Цель работы: Изучить различные способы построения правильных многоугольников.Познакомиться с геометрией циркуля, изучающей геометрические построения одним циркулем.Изучить систему компьютерного черчения КОМПАС
Слайд 2Цель работы:
Изучить различные способы построения правильных многоугольников.
Познакомиться с геометрией циркуля, изучающей
геометрические построения одним циркулем.
Изучить систему компьютерного черчения КОМПАС
Изучить систему компьютерного черчения КОМПАС
Слайд 3Теорема Гаусса — Ванцеля
правильный n - угольник возможно построить с помощью циркуля и
линейки тогда и только тогда, когда
где pi — различные простые числа Ферма, т.е. числа вида
(3, 5, 17, 257, 65537).
Таким образом, построение с помощью циркуля и линейки возможно при n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, ...
и невозможно при n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33, ...
где pi — различные простые числа Ферма, т.е. числа вида
(3, 5, 17, 257, 65537).
Таким образом, построение с помощью циркуля и линейки возможно при n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, ...
и невозможно при n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33, ...
Слайд 4Задача. В данную окружность вписать правильный пятнадцатиугольник.
Построение.Пусть дана окружность радиуса R
с центром О и АВ - сторона правильного вписанного в эту окружность десятиугольника, а АС- сторона правильного вписанного шестиугольника.
Возьмем на окружности произвольную точку A1 и, пользуясь циркулем, отметим на этой окружности последовательно точки А2, A3,..., А15 так, что А1А2 = А2А3 = ... = =A14A15 = ВС. Проведя затем отрезки А1А2, А2А3, А14А15, А15А1, получим искомый правильный пятнадцатиугольник
А 1А2 ... А15
Дуга АВ = 36°, дуга АС = 60° , значит, дуга ВС = 24° .
Т.к. ∠ВОС = 360° / 15= 24° , значит, отрезок ВС - сторона правильного пятнадцатиугольника, вписанного в окружность.
Возьмем на окружности произвольную точку A1 и, пользуясь циркулем, отметим на этой окружности последовательно точки А2, A3,..., А15 так, что А1А2 = А2А3 = ... = =A14A15 = ВС. Проведя затем отрезки А1А2, А2А3, А14А15, А15А1, получим искомый правильный пятнадцатиугольник
А 1А2 ... А15
Дуга АВ = 36°, дуга АС = 60° , значит, дуга ВС = 24° .
Т.к. ∠ВОС = 360° / 15= 24° , значит, отрезок ВС - сторона правильного пятнадцатиугольника, вписанного в окружность.
Слайд 5Задача. Построить правильный семнадцатиугольник.
Строим окружность (O, OA).
Проводим её диаметр AB.
Строим к
нему перпендикуляр m, пересекающий окружность в точках C и D.
Отмечаем точку E — середину DO.
Посередине EO отмечаем точку F и проводим отрезок FA.
Строим биссектрису w₁ ∠OFA.
Строим w₂ — биссектрису угла между m и w₁, которая пересекает AB в точке G.
Проводим s — перпендикуляр к w₂ из точки F.
Строим w₃ — биссектрису угла между s и w₂. Она пересекает AB в точке H.
Строим окружность k₂ на диаметре HA. Она пересекается с CD в точках J и K.
Проводим окружность k₃ с центром G через точки J и K. Она пересекается с AB в точках L и N.
Строим касательную к k₃ через N.
Точки пересечения этой касательной с исходной окружностью (O, OA) — это точки P₃ и P₁₄ искомого семнадцатиугольника. Если принять середину получившейся дуги за P₀ и отложить дугу P₀P₁₄ по окружности три раза, все вершины семнадцатиугольника будут построены.
Отмечаем точку E — середину DO.
Посередине EO отмечаем точку F и проводим отрезок FA.
Строим биссектрису w₁ ∠OFA.
Строим w₂ — биссектрису угла между m и w₁, которая пересекает AB в точке G.
Проводим s — перпендикуляр к w₂ из точки F.
Строим w₃ — биссектрису угла между s и w₂. Она пересекает AB в точке H.
Строим окружность k₂ на диаметре HA. Она пересекается с CD в точках J и K.
Проводим окружность k₃ с центром G через точки J и K. Она пересекается с AB в точках L и N.
Строим касательную к k₃ через N.
Точки пересечения этой касательной с исходной окружностью (O, OA) — это точки P₃ и P₁₄ искомого семнадцатиугольника. Если принять середину получившейся дуги за P₀ и отложить дугу P₀P₁₄ по окружности три раза, все вершины семнадцатиугольника будут построены.
Слайд 6Построение правильного
девятиугольника
Способ приближённого построения был предложен Альбрехтом Дюрером :
«Девятиугольник весьма
часто находится с помощью треугольника следующим образом. Я описываю из центра достаточно большой круг, в котором посредством неизменного круга очерчены рыбьи пузыри, верхний конец которых на окружности есть В, а остальные по бокам суть С, D. Сделав это, проведи прямую линию АВ и раздели её в точках G и Н на три равных промежутка, так что G - ближайшая к самой А. Через эту отметку G проведи линию, пересекающую перпендикуляр АВ под прямым углом, и там, где эта секущая разрезает линию пузыря с обеих сторон, обозначь Е и F. Теперь возьми циркуль, одна ножка которого помещена в центр А, другая - на отметку Е, проведи через F круговую линию, и длина EF обойдёт внутри этой окружности девять раз»
Слайд 7Теорема Мора — Маскерони
Все построения, выполненные с помощь циркуля и линейки, могут быть
проделаны только с помощью циркуля (при этом мы считаем прямую построенной, если найдены хотя бы две точки этой прямой).
В геометрии циркуля прямая линия или отрезок определяется двумя точками, а не задаётся в виде непрерывной прямой линии (проведённой с помощью линейки).
Введём обозначения:
(АВ) - прямая линия, проходящая через две точки А и В;
[АВ] - отрезок АВ;
|АВ| - расстояние между точками А и В;
(О, г) - окружность или круг с центром О и радиусом г;
(А, |ВС|) - окружность или круг с центром А и радиусом г = |ВС|
В геометрии циркуля прямая линия или отрезок определяется двумя точками, а не задаётся в виде непрерывной прямой линии (проведённой с помощью линейки).
Введём обозначения:
(АВ) - прямая линия, проходящая через две точки А и В;
[АВ] - отрезок АВ;
|АВ| - расстояние между точками А и В;
(О, г) - окружность или круг с центром О и радиусом г;
(А, |ВС|) - окружность или круг с центром А и радиусом г = |ВС|
Слайд 8Задача. Построить отрезок, четвёртый пропорциональный к трем данным отрезкам.
Дано: а, b,
с - отрезки. Построить отрезок х, такой, чтобы а : b = с : х.
Построение. Берём произвольную точку О и проводим окружности (О, а) и (О, b). Из произвольной точки А на окружности (О, а) описываем (А, с) и отмечаем точку В пересечения её с окружностью (О, а). Если теперь провести две окружности (A, d) и (В, d) произвольного радиуса d > |а - b|, пересекающие (О, b) в точках A1и B1, то отрезок х = | A1 B1| - искомый .
Построение. Берём произвольную точку О и проводим окружности (О, а) и (О, b). Из произвольной точки А на окружности (О, а) описываем (А, с) и отмечаем точку В пересечения её с окружностью (О, а). Если теперь провести две окружности (A, d) и (В, d) произвольного радиуса d > |а - b|, пересекающие (О, b) в точках A1и B1, то отрезок х = | A1 B1| - искомый .
Слайд 9Доказательствo:
∆AOA1 = ∆ BOB1 (no трем сторонам), поэтому ∠AOA1= ∠ BOB1
и
∠ АОВ = ∠ A1OB1.
Равнобедренные треугольники АОВ и A1OB1подобны (по второму признаку), следовательно, а : b = с : |A1B1|.
∠ АОВ = ∠ A1OB1.
Равнобедренные треугольники АОВ и A1OB1подобны (по второму признаку), следовательно, а : b = с : |A1B1|.
Слайд 10
Задача Л. Маскерони. Построить отрезок в раз
больше заданного. n = 1, 2, 3, .., 25
Проводим окружность (A,|AB|) и отмечаем на ней точку B. Строим точку E, диаметрально противоположную точке B.
Слайд 12Описываем окружности (B,|AF|) и (E,|AF|), которые пересекут окружность(A,|AB|) в точках H
и H1, а окружности (B,|BD|) и (E,|CE|) в точках N и N1, M и M1
Слайд 13Отмечаем точки P, P1, Q, Q1 пересечения окружностей (E,|AE|) и (B,|AB|)
с окружностями (B,|AF|) и (E,|AF|)
Слайд 14Окружности (P,|BP|) и (P1,|BP1|) пересекутся в точке R, а окружность (A,|AB|)
они пересекут в точках S и S1.
Слайд 15Окружности (Q,|EQ|) и (Q1,|EQ1|) пересекутся в точке T, а окружность (A,|AB|)
они пересекут в точках O и O1.
Слайд 16Проводим окружности (R,|AB|) и (F1,|AB|) и отмечаем точки L, L1, G
пересечения их с окружностью (A,|AB|)
Слайд 27Вывод
В работе рассмотрен раздел геометрии – геометрия циркуля, показана красота и
занимательность задач на построение.
При работе над темой для выполнения построений была использована система компьютерного черчения КОМПАС, что позволило добиться максимальной точности и аккуратности работы.
При работе над темой для выполнения построений была использована система компьютерного черчения КОМПАС, что позволило добиться максимальной точности и аккуратности работы.