№15)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ЕГЭ. Решение задач на производную и первообразную (Задания №8 и №14)
Содержание
- 1. Подготовка к ЕГЭ. Решение задач на производную и первообразную (Задания №8 и №14)
- 2. Чтобы найти, в какой момент времени t скорость была равна 4 м/с, решим уравнение:Ответ: 3.Задача 1
- 3. На рисунке изображен график производной функции f(x).
- 4. Поскольку касательная параллельна прямой y = 6x или совпадает
- 5. На рисунке изображён график функции y=f(x) и
- 6. Значение производной в точке касания равно угловому
- 7. Решение.Найдем производную заданной функции: Найденная производная неотрицательна
- 8. на отрезке [-29; -27]Решение.Найдем производную заданной функции:
Чтобы найти, в какой момент времени t скорость была равна 4 м/с, решим уравнение:Ответ: 3.Задача 1
Слайд 2Чтобы найти, в какой момент времени t скорость была равна 4 м/с,
решим уравнение:
Ответ: 3.
Задача 1
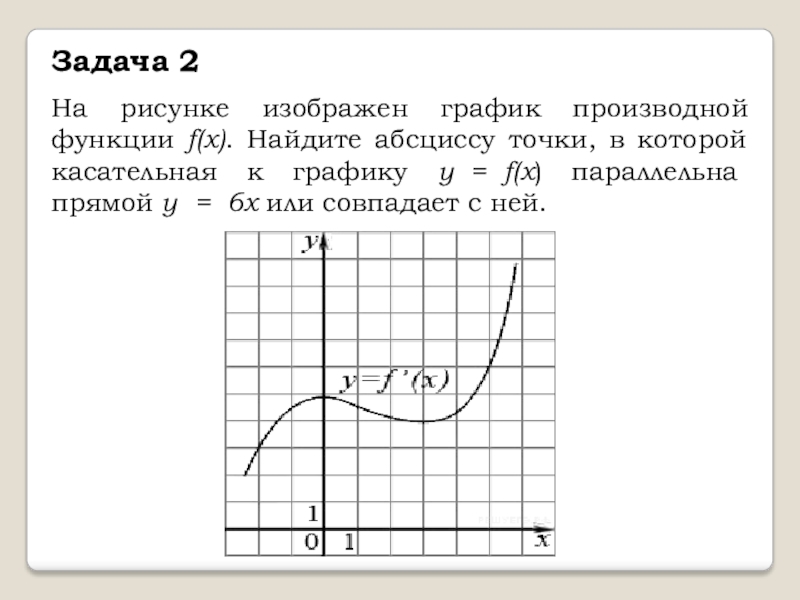
Слайд 3На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в
которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
Задача 2
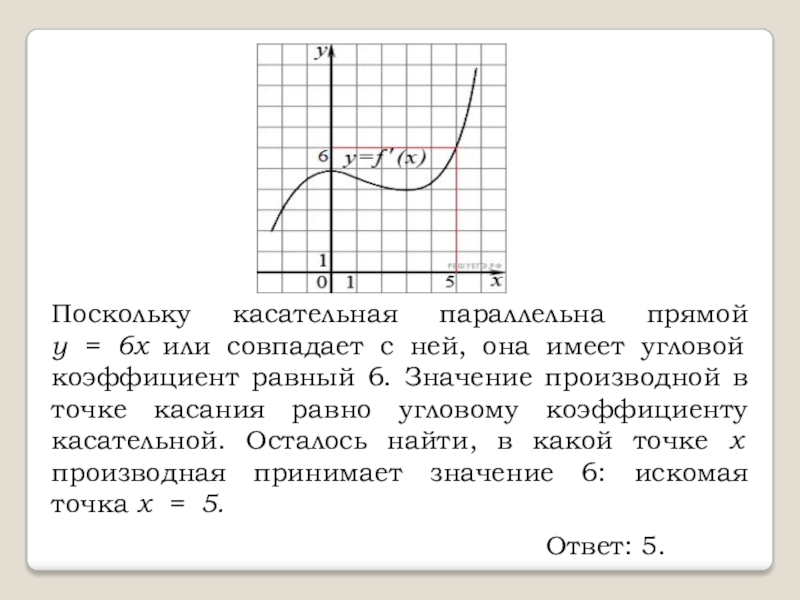
Слайд 4Поскольку касательная параллельна прямой y = 6x или совпадает с ней, она имеет
угловой коэффициент равный 6. Значение производной в точке касания равно угловому коэффициенту касательной. Осталось найти, в какой точке x производная принимает значение 6: искомая точка x = 5.
Ответ: 5.
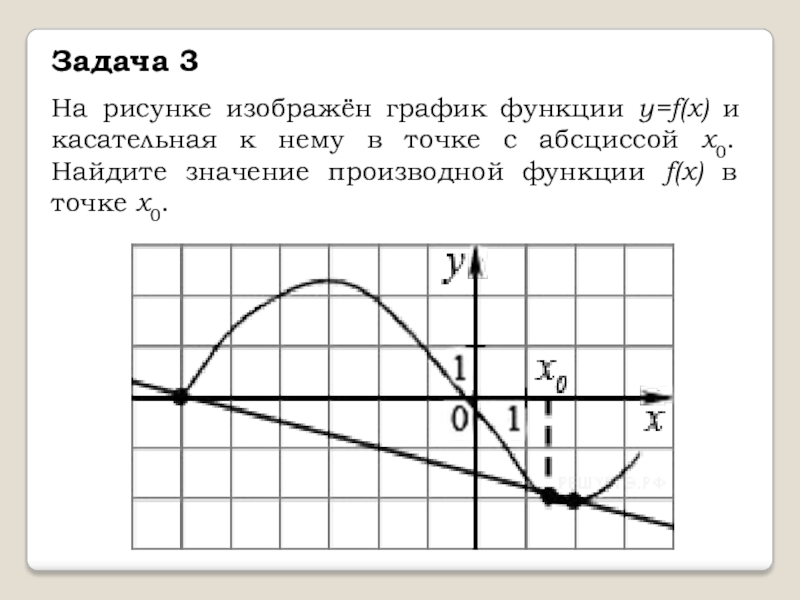
Слайд 5На рисунке изображён график функции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Задача 3
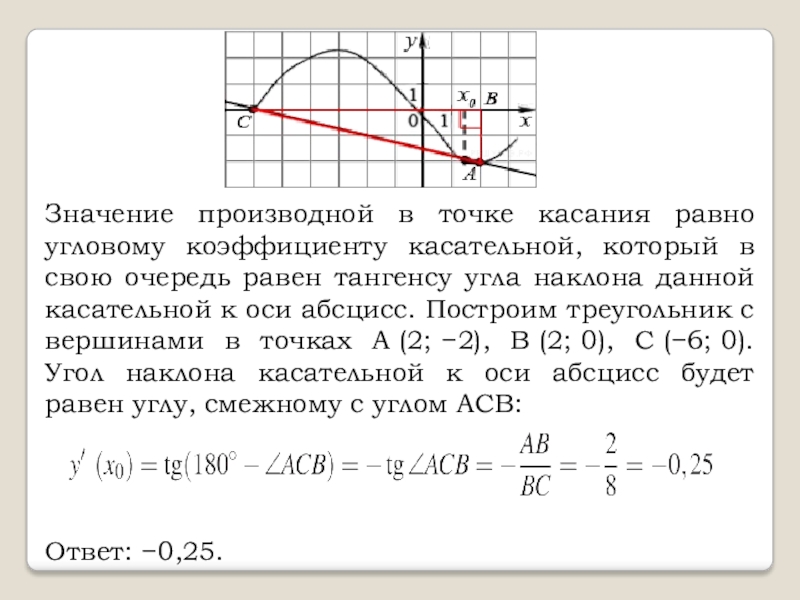
Слайд 6Значение производной в точке касания равно угловому коэффициенту касательной, который в
свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:
Ответ: −0,25.
Слайд 7Решение.
Найдем производную заданной функции:
Найденная производная неотрицательна на заданном отрезке, заданная
функция возрастает на нем, поэтому наибольшим значением функции на отрезке является
Задача 4
Слайд 8на отрезке [-29; -27]
Решение.
Найдем производную заданной функции:
Решая уравнение y’ =
0, находим x = -30, х = -28 . Определим знаки производной функции и изобразим на рисунке поведение функции на заданном отрезке:
Ответ: 4.
Задача 5



![Подготовка к ЕГЭ. Решение задач на производную и первообразную (Задания №8 и №14) на отрезке [-29; -27]Решение.Найдем производную заданной функции: Решая уравнение y’ = на отрезке [-29; -27]Решение.Найдем производную заданной функции: Решая уравнение y’ = 0, находим x = -30, х](/img/thumbs/76465802f0a70b34e6c952faa703eef0-800x.jpg)





