- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Основы логики. Логические операции
Содержание
- 1. Основы логики. Логические операции
- 2. Логика – эта наука о формах и способах мышления
- 3. Этапы развития логики1-й этап связан с работами
- 4. 2-й этап – появление математической, или символической,
- 5. Но он выдвинул только идею,
- 6. Формы мышления. Понятие – это форма мышления,
- 7. Суждение (высказывание, утверждение) – это форма мышления,
- 8. Умозаключение – это форма мышления, с помощью
- 9. Алгебра высказываний В алгебре высказываний высказывания обозначаются
- 10. Пример 1 Например, содержание понятия персональный компьютер-это
- 11. Пример 21. Истинное и простое высказывание: Буква
- 12. Пример 3Все металлы – простые вещества.Литий – металл. Литий – простое вещество.
- 13. Пример 4А= “Листва на деревьях опадает осенью”. А=1 В= “Земля прямоугольная”. В=0
- 14. ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- 15. Логическая операция – способ построения
- 16. Конъюнкция (логическое умножение) Конъюнкция двух логических
- 17. Таблица истинности
- 18. Дизъюнкция (логическое сложение) Дизъюнкция
- 19. Таблица истинности
- 20. Инверсия (логическое отрицание) Инверсия логической переменной истина,
- 21. Таблица истинности
- 22. Импликация (логическое следование) Импликация двух логических
- 23. Таблица истинности
- 24. Эквивалентность (логическое равенство) Эквивалентность двух
- 25. Таблица истинности
- 26. Приоритет выполнения логических операций При
- 27. ПримерДана формулаПостроить таблицу истинности.
Логика – эта наука о формах и способах мышления
Слайд 3Этапы развития логики
1-й этап связан с работами ученого и философа Аристотеля
(384-322 г.г. до н.э.). Он пытался найти ответ на вопрос “Как мы рассуждаем”, изучал правила мышления. Аристотель впервые дал систематическое изложение логики. Он подверг анализу человеческое мышление, его формы – понятие, суждение, умозаключение. Так возникла формальная логика.
Слайд 42-й этап – появление математической, или символической, логики. Основы ее заложил
немецкий ученый и философ Г.В. Лейбниц (1646-1716). Он сделал попытку построить первые логические исчисления, считал, что можно заменить простые рассуждения действиями со знаками, и привел соответствующие правила.
Слайд 5 Но он выдвинул только идею, а развил её окончательно
англичанин Д. Буль (1815-1864).
Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику.
Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику.
Слайд 6Формы мышления.
Понятие – это форма мышления, фиксирующая основные, существенные признаки
объекта.
Понятие имеет две стороны: содержание и объем.
Содержание понятия – совокупность существенных признаков, отраженных в этом понятии.
Объем понятия – множество предметов, каждому из которых принадлежат признаки, составляющие
содержание понятий.
Пример
Понятие имеет две стороны: содержание и объем.
Содержание понятия – совокупность существенных признаков, отраженных в этом понятии.
Объем понятия – множество предметов, каждому из которых принадлежат признаки, составляющие
содержание понятий.
Пример
Слайд 7Суждение (высказывание, утверждение) – это форма мышления, в которой что-либо утверждается
или отрицается о свойствах реальных предметов и отношениях между ними.
Высказывание может быть либо истинным, либо ложным, и может быть либо простым, либо составным (сложным).
Пример
Высказывание может быть либо истинным, либо ложным, и может быть либо простым, либо составным (сложным).
Пример
Слайд 8Умозаключение – это форма мышления, с помощью которой из одного или
нескольких суждений может быть получено новое суждение (ВЫВОД).
Слайд 9Алгебра высказываний
В алгебре высказываний высказывания обозначаются именами логических переменных, которые
могут принимать лишь два значения: “истинна” (1) и “ложь” (0).
Слайд 10Пример 1
Например, содержание понятия персональный компьютер-это универсальное электронное устройство для
автоматической обработки информации, предназначенное для одного пользователя.
Объем понятия персональный компьютер – совокупность существующих в мире персональных компьютеров.
Объем понятия персональный компьютер – совокупность существующих в мире персональных компьютеров.
Слайд 11Пример 2
1. Истинное и простое высказывание: Буква “т” - согласная.
2.
Ложное и сложное высказывание: Осень наступила, и грачи прилетели.
Слайд 15 Логическая операция – способ построения сложного высказывания из данных
высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
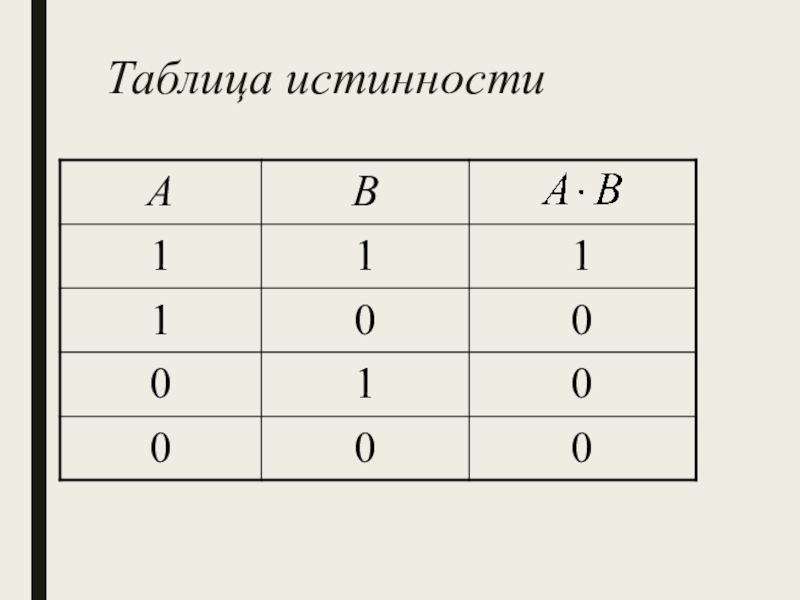
Слайд 16Конъюнкция (логическое умножение)
Конъюнкция двух логических переменных истинна тогда
и только тогда, когда оба высказывания, истинны.
Обозначение:
Имеет смысловую нагрузку «и»
Обозначение:
Имеет смысловую нагрузку «и»
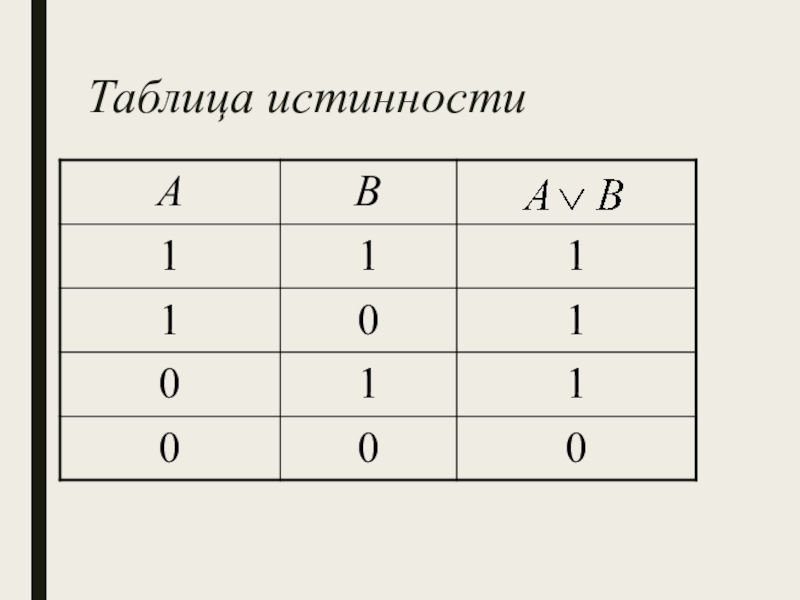
Слайд 18 Дизъюнкция (логическое
сложение)
Дизъюнкция двух логических переменных ложна
тогда и только тогда, когда оба высказывания ложны.
Обозначение:
Имеет смысловую нагрузку «или»
Обозначение:
Имеет смысловую нагрузку «или»
Слайд 20Инверсия (логическое отрицание)
Инверсия логической переменной истина, если переменная ложна, и,
наоборот, инверсия ложна, если переменная истинна.
Обозначение:
Имеет смысловую нагрузку «не»
Обозначение:
Имеет смысловую нагрузку «не»
Слайд 22Импликация (логическое следование)
Импликация двух логических переменных ложна тогда и
только тогда, когда из истинного основания следует ложное следствие.
Обозначение:
А - условие
В - следствие
Имеет смысловую нагрузку
«если…., то…»
Обозначение:
А - условие
В - следствие
Имеет смысловую нагрузку
«если…., то…»
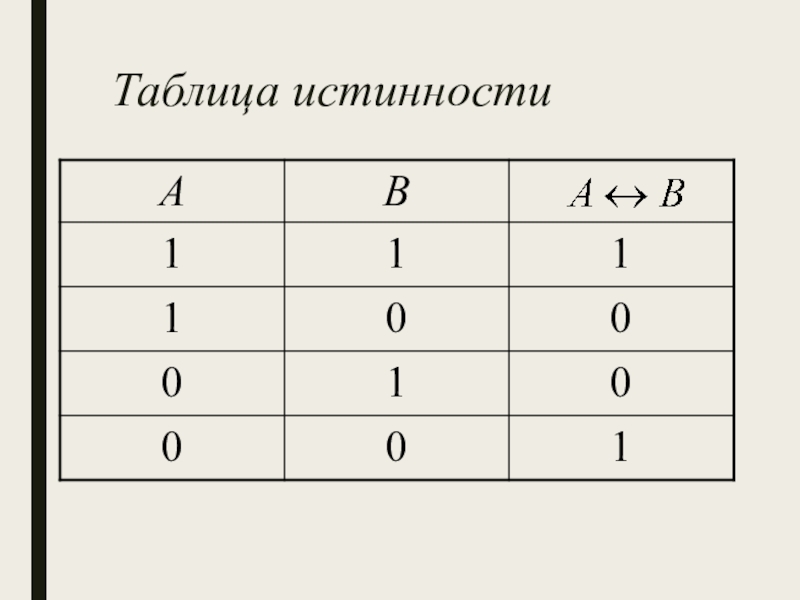
Слайд 24 Эквивалентность (логическое равенство)
Эквивалентность двух логических переменных истинна
тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Обозначение:
Имеет смысловую нагрузку «тогда и только тогда»
Обозначение:
Имеет смысловую нагрузку «тогда и только тогда»
Слайд 26Приоритет выполнения логических операций
При вычислении значения логического выражения
(формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
1.инверсия,
2.конъюнкция,
3.дизъюнкция,
4.импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Пример
1.инверсия,
2.конъюнкция,
3.дизъюнкция,
4.импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Пример