- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Основы формальная и математической логики. Таблицы истинности. 11 класс
Содержание
- 1. Основы формальная и математической логики. Таблицы истинности. 11 класс
- 2. Сложные логические выражения- получаются из простых и
- 3. Таблицы истинности сложных логических выражений Алгоритм
- 4. Пример. Определить таблицу истинности логической функции: F(A,
- 5. Записать в виде логического выражения, построить таблицы
- 6. Домашнее задание. Записать в виде логического выражения,
Сложные логические выражения- получаются из простых и сложных с использованием логических операций. Приоритет выполнения операций: 1.инверсия, 2.конъюнкция, 3.дизъюнкция, 4.импликация, 5.эквивалентность, 6.строгая дизъюнкцияПорядок операций может задаваться скобками (А∨В) & (A∨C)Инверсия над сложным выражением выполняет роль
Слайд 2Сложные логические выражения-
получаются из простых и сложных с использованием логических
операций.
Приоритет выполнения операций: 1.инверсия, 2.конъюнкция, 3.дизъюнкция, 4.импликация, 5.эквивалентность, 6.строгая дизъюнкция
Порядок операций может задаваться скобками
(А∨В) & (A∨C)
Инверсия над сложным выражением выполняет роль скобок
А∨A&В & A∨C
Приоритет выполнения операций: 1.инверсия, 2.конъюнкция, 3.дизъюнкция, 4.импликация, 5.эквивалентность, 6.строгая дизъюнкция
Порядок операций может задаваться скобками
(А∨В) & (A∨C)
Инверсия над сложным выражением выполняет роль скобок
А∨A&В & A∨C
Слайд 3Таблицы истинности
сложных логических выражений
Алгоритм построения
Определить количество наборов входных переменных
в выражении: Q=2n, где n – количество входных переменных;
Внести в таблицу все наборы входных переменных
Определить количество логических операций и порядок их выполнения;
Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности
Внести в таблицу все наборы входных переменных
Определить количество логических операций и порядок их выполнения;
Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности
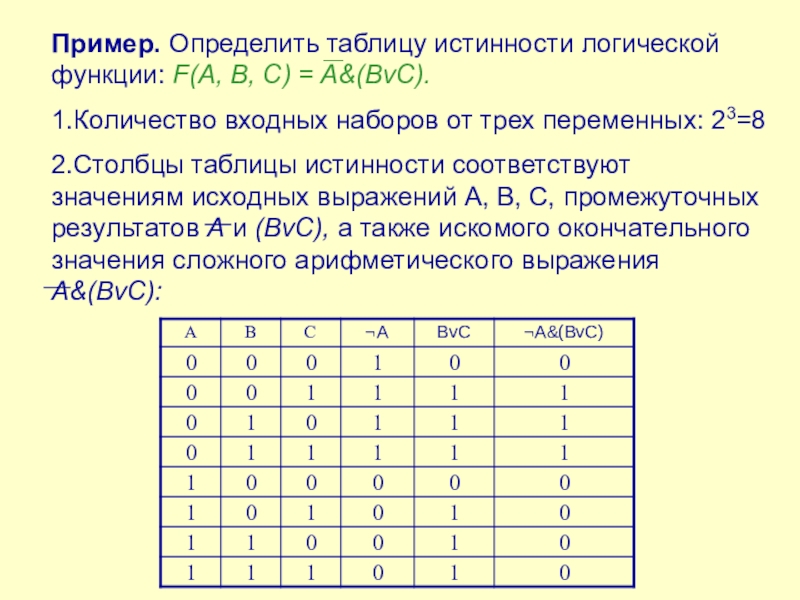
Слайд 4Пример. Определить таблицу истинности логической функции: F(A, B, C) = A&(BvC).
1.Количество
входных наборов от трех переменных: 23=8
2.Столбцы таблицы истинности соответствуют значениям исходных выражений A, B, C, промежуточных результатов A и (BvC), а также искомого окончательного значения сложного арифметического выражения A&(BvC):
2.Столбцы таблицы истинности соответствуют значениям исходных выражений A, B, C, промежуточных результатов A и (BvC), а также искомого окончательного значения сложного арифметического выражения A&(BvC):
Слайд 5Записать в виде логического выражения, построить таблицы истинности, при каких значениях
функция истинна:
F(A,B) = неА и неВ
F(A,B) = не(неА или В) и неВ
F(A,B,С) = не(А или неС) и не(С или неВ)
F(A,B,С) = не(неА и не(В и неС))
F(A,B)= не(А и B) ↔ (неА или В)
F(A,B) = неА и неВ
F(A,B) = не(неА или В) и неВ
F(A,B,С) = не(А или неС) и не(С или неВ)
F(A,B,С) = не(неА и не(В и неС))
F(A,B)= не(А и B) ↔ (неА или В)
Задания
Слайд 6Домашнее задание.
Записать в виде логического выражения, построить таблицы истинности, при
каких значениях функция истинна:
F(A,B,С)= (А или В) и C →А и B
F(X,Y,Z) =не(не(неX или неZ) и (X или неY))
F(M,N,K) = не(не(M и K и N) или неM и неN и неK)