- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Общие сведения о системах счисления
Содержание
- 1. Общие сведения о системах счисления
- 2. *Система счисления - Это знаковая система, в
- 3. Все системы счисления делятся на две большие
- 4. В римской системе счисления семь
- 5. Основанием позиционной системы счисления называется целое число,
- 6. Слайд 6
- 7. Любое целое число можно представить в виде
- 8. ЗАДАНИЕ: ЗАПИСАТЬ ЧИСЛА В РАЗВЁРНУТОМ ВИДЕ.10012 1456 21358 1A51627,48101012=1*24+0*23+1*22+0*21+1*20
- 9. 1. Перевод целых чисел из десятичной системы
- 10. *Последовательно выполнять деление исходного целого десятичного числа
- 11. *48 10= X210510 = X220410 = X2ПЕРЕВЕДИТЕ ЧИСЛА:
- 12. *Последовательно выполнять деление исходного целого десятичного числа
- 13. *ПЕРЕВЕДИТЕ ЧИСЛА:48 10= X810510 = X820410 = X8
- 14. *Последовательно выполнять деление исходного целого десятичного числа
- 15. *ПЕРЕВЕДИТЕ ЧИСЛА:48 10= X1610510 = X1620410 = X16
- 16. ПЕРЕВОД ДВОИЧНОГО ЧИСЛА В ДЕСЯТИЧНОЕ
- 17. *1011012 = X101101112 = X1011110012 = X10ПЕРЕВЕДИТЕ ЧИСЛА:
- 18. ПЕРЕВОД ВОСЬМЕРИЧНОГО ЧИСЛА В ДЕСЯТИЧНОЕ
- 19. *1238 = X10178 = X101568 = X10ПЕРЕВЕДИТЕ ЧИСЛА:
- 20. ПЕРЕВОД 16-ГО ЧИСЛА В ДЕСЯТИЧНОЕ
- 21. *1F16 = X10AB16 = X109D16 = X10ПЕРЕВЕДИТЕ ЧИСЛА:
- 22. Для преобразования десятичных дробей в число любой
- 23. Если число Х имеет целую и дробную
- 24. *Перевод чисел из двоичной системы счисления в
- 25. *Перевод чисел из двоичной системы счисления в
- 26. * Перевод чисел из восьмеричной и шестнадцатеричной
- 27. Арифметические операции в позиционных системах счисления
- 28. *Сложение чисел в двоичной системе счисления.Обратите внимание
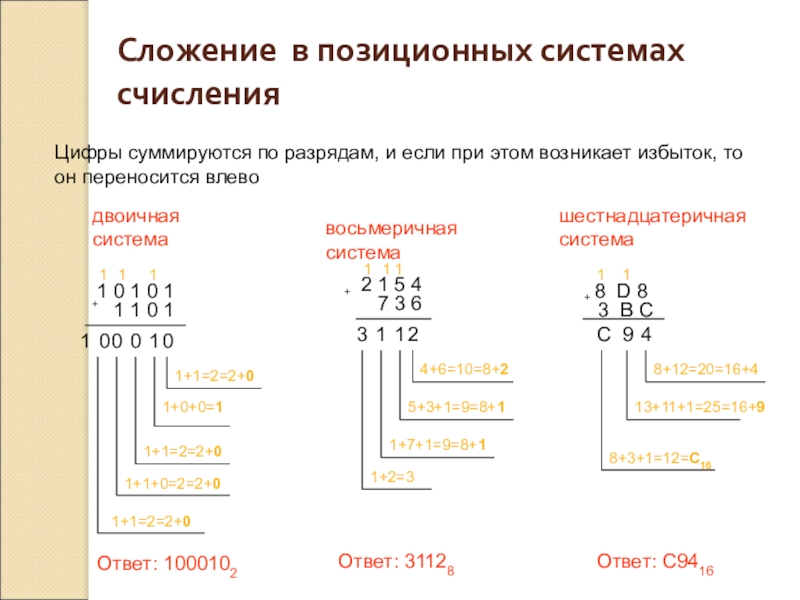
- 29. Сложение в позиционных системах счисления
- 30. *Вычитание чисел в двоичной системе счисленияОбратите внимание
- 31. Вычитание в позиционных системах счисления
- 32. УМНОЖЕНИЕ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ
- 33. ДЕЛЕНИЕ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ
- 34. ЗАДАНИЯ ИЗ ЕГЭ Сколько единиц в двоичной записи числа 195?5234
- 35. Количество значащих нулей в двоичной записи десятичного числа 129 равно:5674Задания из ЕГЭ
- 36. Как представлено число 7510 в двоичной системе счисления?100101121001012110100121111012Задания из ЕГЭ
- 37. Количество цифр в двоичной записи десятичного числа, которое можно представить в виде 2+8+16+64+128+256+512, равно78910Задания из ЕГЭ
- 38. №1 Мартышка-мама связала 111 - ти
- 39. Мартышка висит на хвосте и жует бананы.
- 40. До новых встреч с занимательными задачами
Слайд 1СИСТЕМЫ СЧИСЛЕНИЯ
10 класс
Автор: Глухова Татьяна Ивановна-
учитель информатики МБОУ Салганской СОШ
Слайд 2*
Система счисления -
Это знаковая система, в которой числа записываются по
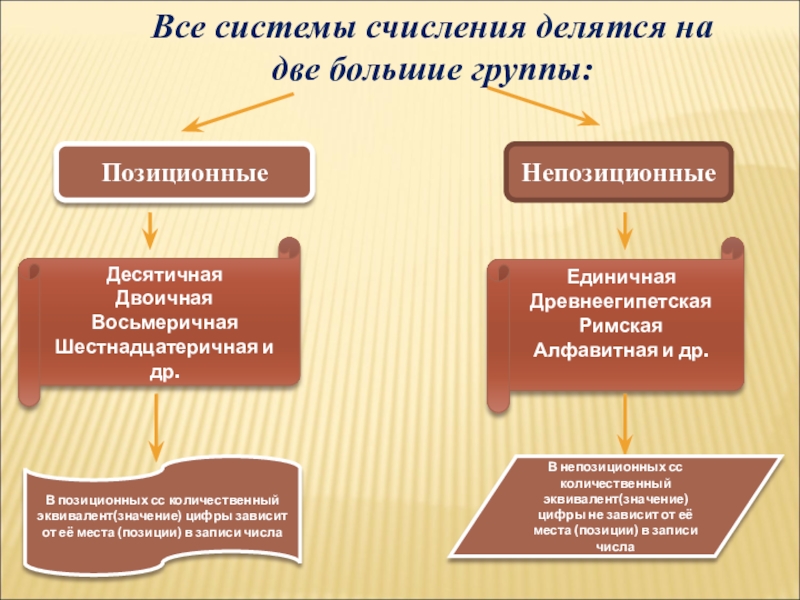
Слайд 3Все системы счисления делятся на две большие группы:
Позиционные
Непозиционные
Единичная
Древнеегипетская
Римская
Алфавитная
Десятичная
Двоичная
Восьмеричная
Шестнадцатеричная и др.
В позиционных сс количественный эквивалент(значение) цифры зависит от её места (позиции) в записи числа
В непозиционных сс количественный эквивалент(значение) цифры не зависит от её места (позиции) в записи числа
Слайд 4
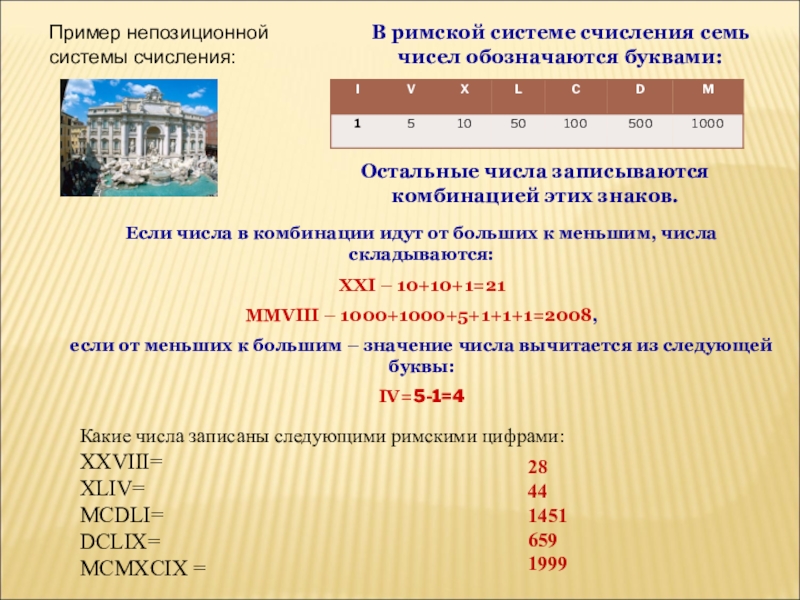
В римской системе счисления семь чисел обозначаются буквами:
Остальные
Если числа в комбинации идут от больших к меньшим, числа складываются:
XXI – 10+10+1=21
MMVIII – 1000+1000+5+1+1+1=2008,
если от меньших к большим – значение числа вычитается из следующей буквы:
IV=5-1=4
Пример непозиционной системы счисления:
Какие числа записаны следующими римскими цифрами:
XXVIII=
XLIV=
MCDLI=
DCLIX=
MCMXCIX =
28
44
1451
659
1999
Слайд 5Основанием позиционной системы счисления называется целое число, которое равно количеству цифр,
Десятичная система счисления: основание q=10.
Алфавит: 0,1,2,3,4,5,6,7,8,9. Например: 12710
Двоичная система счисления: основание q=2
Алфавит: 0,1. Например : 100112
Восьмеричная система счисления: основание q=8
Алфавит: 0,1,2,3,4,5,6,7. Например: 2358
Шестнадцатеричная система счисления: основание q=16
Алфавит: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Например: 4F1716
Слайд 7
Любое целое число можно представить в виде суммы разрядных слагаемых –
1652 = 1×1 000 + 6×100 + 5×10 + 2×1
1652=1*103 +6*102+5*101+2*100
РАЗВЁРНУТАЯ ФОРМА ЗАПИСИ ЧИСЛА
1652-свёрнутая форма записи числа
Развёрнутая форма числа
а0=1
Слайд 8ЗАДАНИЕ: ЗАПИСАТЬ ЧИСЛА В РАЗВЁРНУТОМ ВИДЕ.
10012
1456
21358
1A516
27,48
101012=1*24+0*23+1*22+0*21+1*20
Слайд 91. Перевод целых чисел из десятичной системы
Перевод целого десятичного числа
Перевод целого десятичного числа в восьмеричное
Перевод целого десятичного числа в 16-ное
2. Перевод в десятичную систему
Перевод двоичного числа в десятичное
Перевод восьмеричного числа в десятичное
Перевод 16-го числа в десятичное
Слайд 10*
Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных
Записать полученные остатки в обратной последовательности, начиная с последнего неполного частного.
4610→1011102
Пример:
Перевод целого десятичного числа в двоичное:
Слайд 12*
Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных
Записать полученные остатки в обратной последовательности, начиная с последнего неполного частного.
4610→568
01234567
восьмиричная
Пример:
Перевод целого десятичного числа в восьмеричное:
Слайд 14*
Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных
Записать полученные остатки в обратной последовательности, начиная с последнего неполного частного.
4610→2E16
Пример:
Перевод целого десятичного числа в 16-ное:
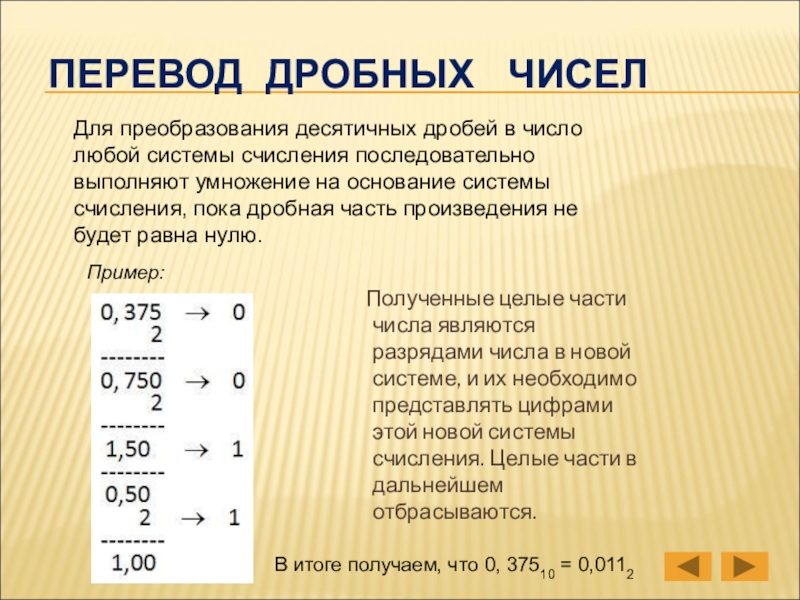
Слайд 22Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют
ПЕРЕВОД ДРОБНЫХ ЧИСЕЛ
Полученные целые части числа являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.
В итоге получаем, что 0, 37510 = 0,0112
Пример:
Слайд 23Если число Х имеет целую и дробную часть, то переводим целую
ПЕРЕВОД СМЕШАННЫХ ЧИСЕЛ
Пример: Перевести число 15, 2510
Значит 15,2510 = 1111,012
Слайд 24*
Перевод чисел из двоичной системы счисления в восьмеричную
Перевод целых чисел:
Для перевода
НАПРИМЕР: 1010012 = 518
Перевод дробных чисел:
Для перевода дробного двоичного числа в восьмеричное необходимо разбить двоичное число на триады слева направо; если в последней правой группе окажется меньше разрядов, надо дополнить справа нулями. Далее нужно триады заменить на восьмеричные числа.
НАПРИМЕР: 0,1101012 = 0,358
Слайд 25*
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Перевод целых чисел:
Для перевода
НАПРИМЕР: ПЕРЕВЕДЁМ ЦЕЛОЕ ДВОИЧНОЕ ЧИСЛО A2 = 1010012
0010 10012 = 29 16
Перевод дробных чисел:
Для перевода дробного двоичного числа в шестнадцатеричное необходимо разбить двоичное число на тетрады слева направо; если в последней правой группе окажется меньше разрядов, надо дополнить справа нулями. Далее нужно триады заменить на восьмеричные числа.
НАПРИМЕР: A2 = 0,1101012
0,1101 01002 = 0,D416
Слайд 26*
Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную:
Например: 1. Преобразуем дробное восьмеричное число A8 = 0,478 в двоичную систему счисления:
0,478 = 0,1001112
2. Переведём целое шестнадцатеричное число A16 = AB16 в двоичную систему счисления:
A16 = 101010112
Слайд 28*
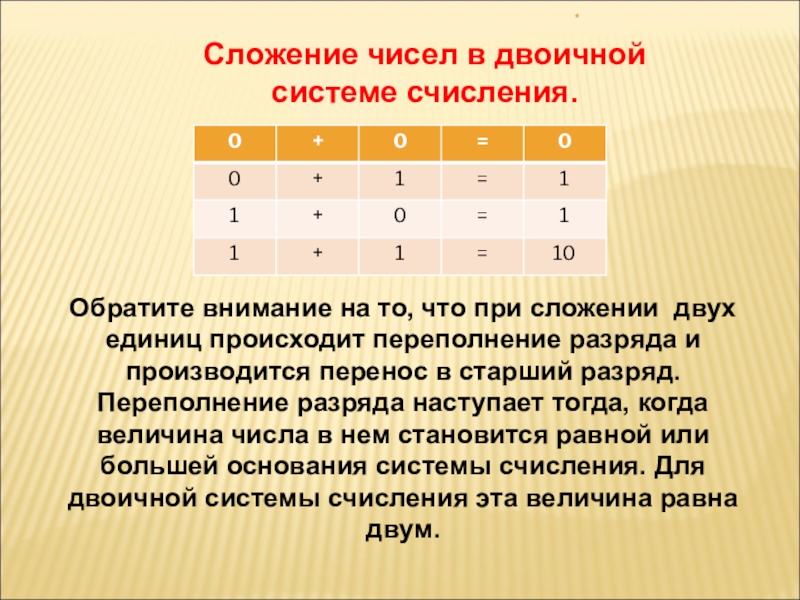
Сложение чисел в двоичной системе счисления.
Обратите внимание на то, что при
Слайд 29Сложение в позиционных системах счисления
Цифры суммируются по
1 0 1 0 1
+
1 1 0 1
двоичная
система
0
1+1=2=2+0
1
1
1+0+0=1
0
1+1=2=2+0
1
0
1+1+0=2=2+0
1
0
1+1=2=2+0
1
Ответ: 1000102
2 1 5 4
+
7 3 6
2
4+6=10=8+2
1
1
5+3+1=9=8+1
1
1+7+1=9=8+1
1
3
1+2=3
восьмеричная
система
1
Ответ: 31128
шестнадцатеричная
система
8 D 8
+
3 B C
4
8+12=20=16+4
1
9
13+11+1=25=16+9
8+3+1=12=C16
C
1
Ответ: C9416
Слайд 30*
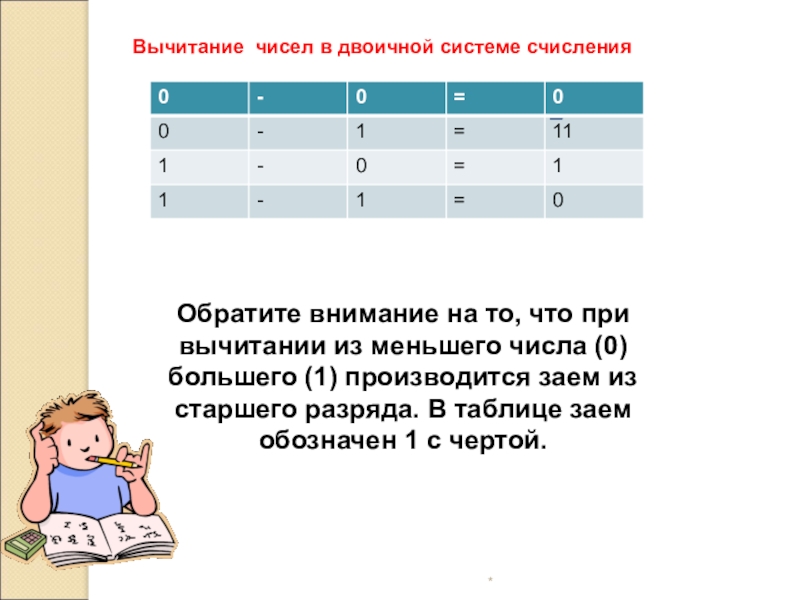
Вычитание чисел в двоичной системе счисления
Обратите внимание на то, что при
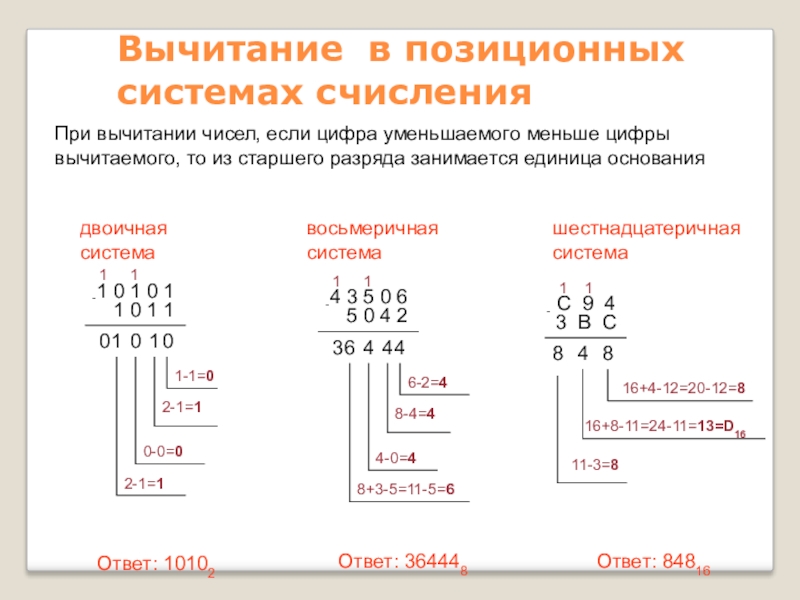
Слайд 31Вычитание в позиционных системах счисления
При вычитании чисел,
двоичная
система
Ответ: 10102
восьмеричная
система
Ответ: 364448
шестнадцатеричная
система
Ответ: 84816
1 0 1 0 1
-
1 0 1 1
0
1-1=0
1
1
2-1=1
0
0-0=0
1
2-1=1
1
0
4 3 5 0 6
-
5 0 4 2
4
6-2=4
1
4
8-4=4
4
4-0=4
6
8+3-5=11-5=6
1
3
С 9 4
-
3 В С
8
16+4-12=20-12=8
1
4
16+8-11=24-11=13=D16
8
11-3=8
1
Слайд 32УМНОЖЕНИЕ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ
При умножении многозначных
двоичная
система
Ответ: 1010111112
1 1 0 1 1
х
1 1 0 1
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 0 1 0 1 1 1 1 1
1+1+1=3=2+1
1
1+1+1=3=2+1
1
1+1=2=2+0
1
1
Слайд 33ДЕЛЕНИЕ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ
Деление в любой
двоичная
система
Ответ: 10,12
1 0 0 0 1 1
1 1 1 0
1
1 1 1 0
1 1 1 0
1 1
1
,
0
0
1
0
Слайд 36Как представлено число 7510 в двоичной системе счисления?
10010112
1001012
11010012
1111012
Задания из ЕГЭ
Слайд 37Количество цифр в двоичной записи десятичного числа, которое можно представить в
7
8
9
10
Задания из ЕГЭ
Слайд 38№1
Мартышка-мама связала 111 - ти своим непослушным детишкам по
Ответ в 8-й сс
Занимательные задачи
Слайд 39
Мартышка висит на хвосте и жует бананы. В каждой руке по
Ответ в 2-й сс
№2