- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мультимедийная разработка по информатике на тему Графы. Поиск путей в графе.
Содержание
- 1. Мультимедийная разработка по информатике на тему Графы. Поиск путей в графе.
- 2. Общие сведения о Графах.Граф – это совокупность объектов со
- 3. Смешанный граф – это граф, содержащий как ориентированные,
- 4. 12Задачи на поиск путей в ГрафеЗадача 1.На
- 5. Решение задачи 1.
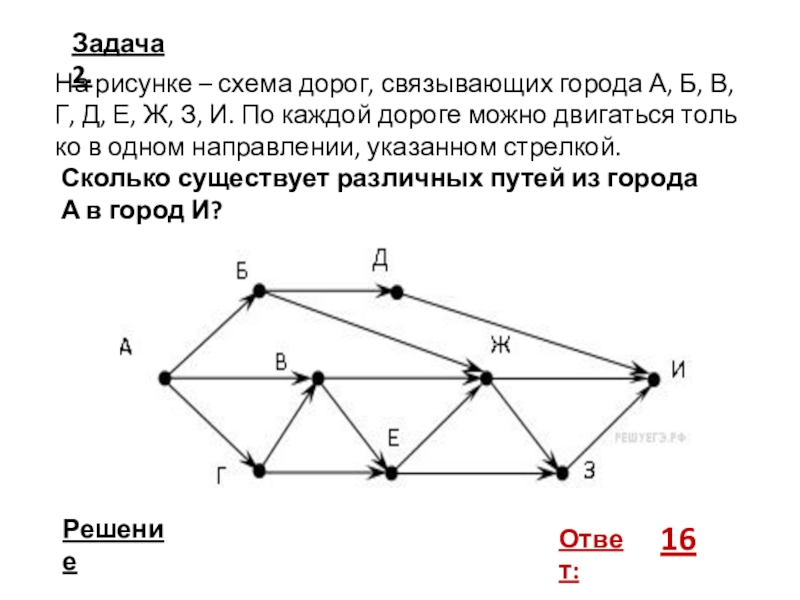
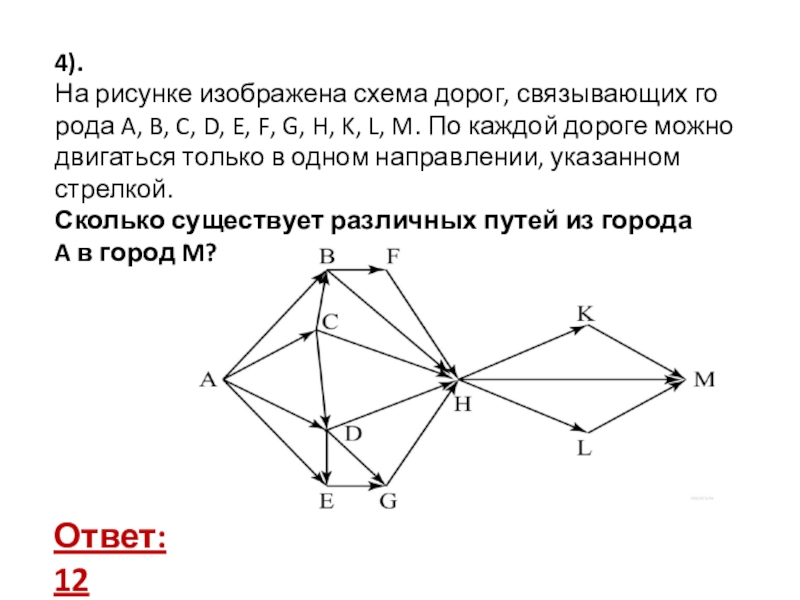
- 6. Задача 2.На рисунке – схема дорог, связывающих
- 7. Решение задачи 2.Начнем считать количество путей с
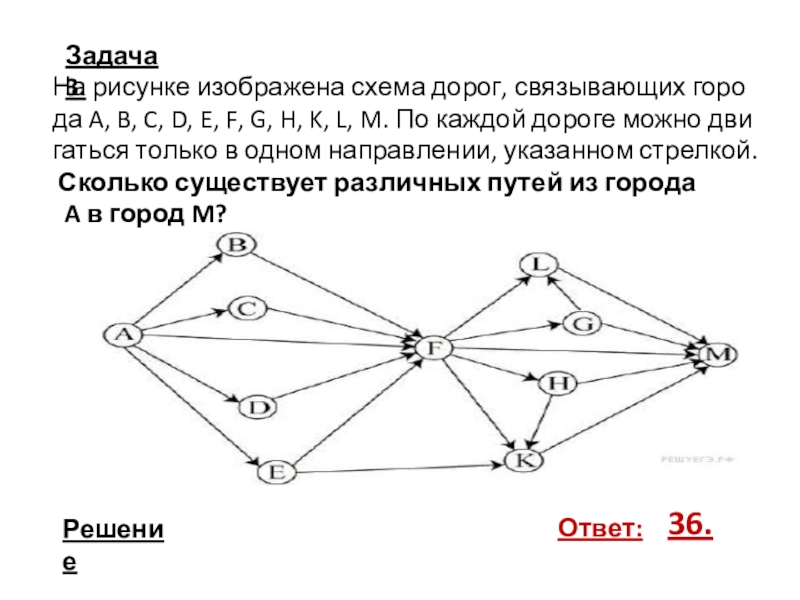
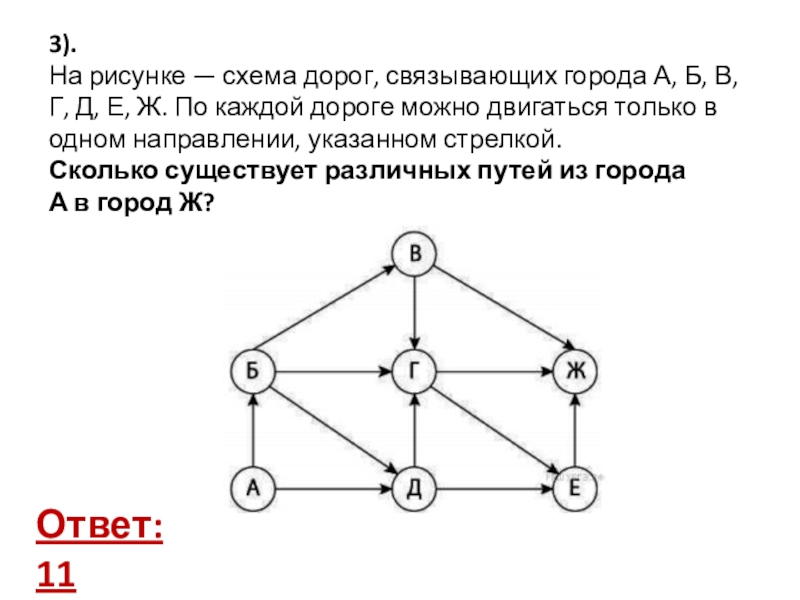
- 8. Задача 3.На рисунке изображена схема дорог, связывающих
- 9. Решение задачи 3.1. Начнем считать количество путей
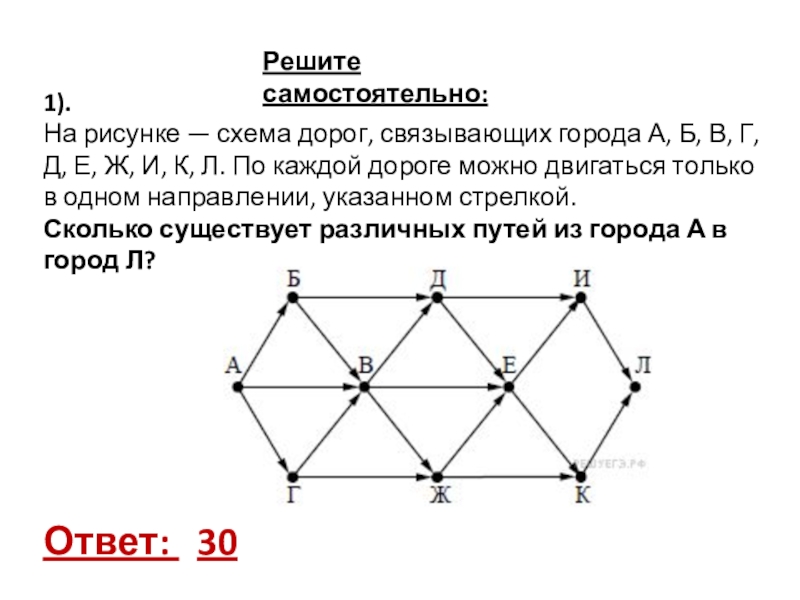
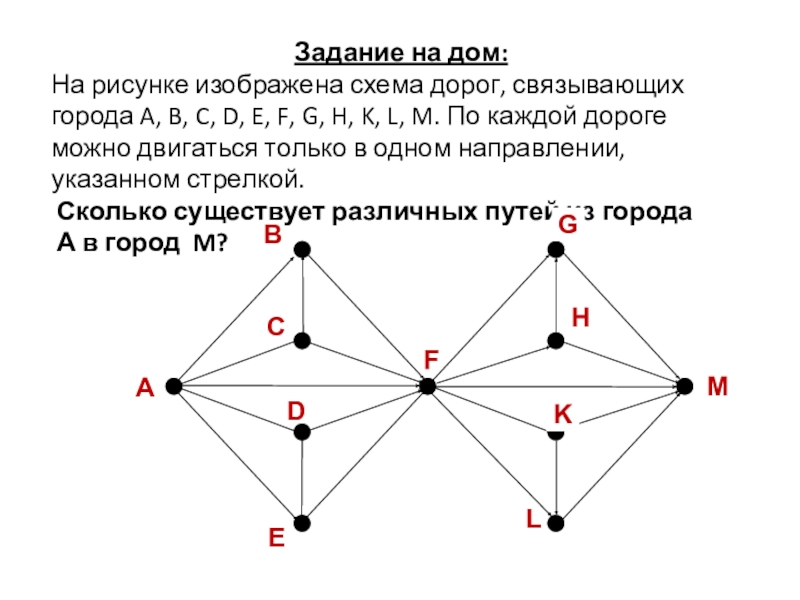
- 10. Решите самостоятельно:Ответ: 30
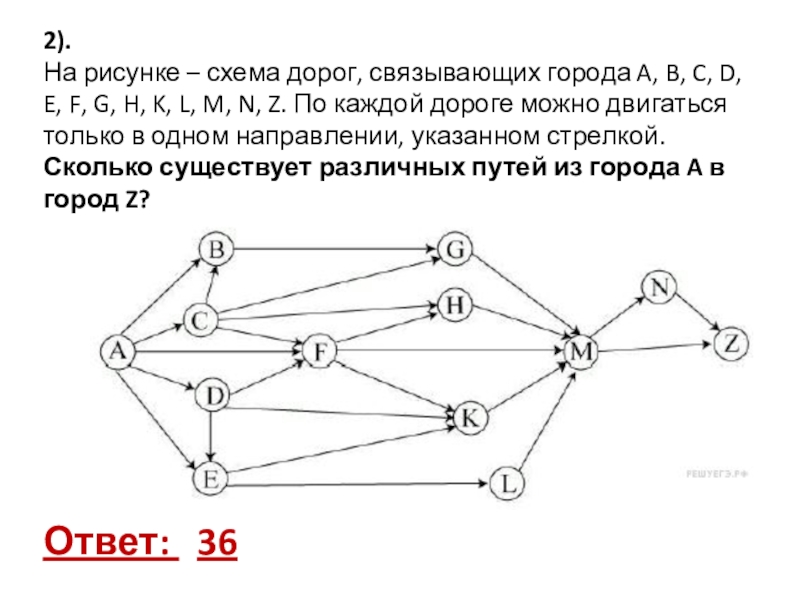
- 11. Ответ: 36
- 12. Ответ: 11
- 13. Ответ: 12
- 14. Слайд 14
- 15. Источники информации:http://www.compress.ru/Archive/CP/2007/1/18/10.gifhttp://im1-tub-ru.yandex.net/i?id=a8d63dcb87271432e78d2783001d5e0b-133-144&n=21http://masters.donntu.edu.ua/2013/fknt/bilyk/diss/index.htm#4http://masters.donntu.edu.ua/2013/fknt/bilyk/diss/images/4.pnghttp://inf.reshuege.ru/test?theme=203http://inf.reshuege.ru/get_file?id=3029
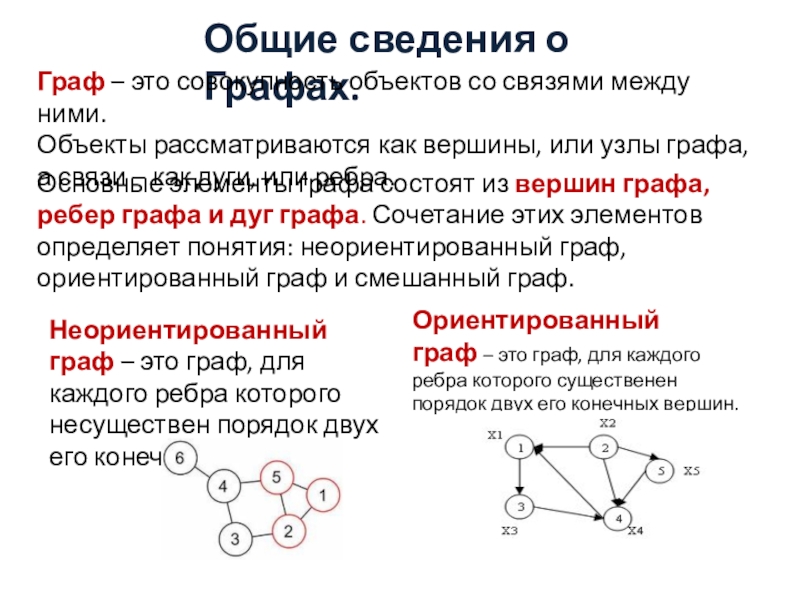
Слайд 2Общие сведения о Графах.
Граф – это совокупность объектов со связями между ними.
Объекты рассматриваются
а связи – как дуги, или ребра.
Основные элементы графа состоят из вершин графа, ребер графа и дуг графа. Сочетание этих элементов определяет понятия: неориентированный граф, ориентированный граф и смешанный граф.
Неориентированный граф – это граф, для каждого ребра которого несуществен порядок двух его конечных вершин.
Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух его конечных вершин.
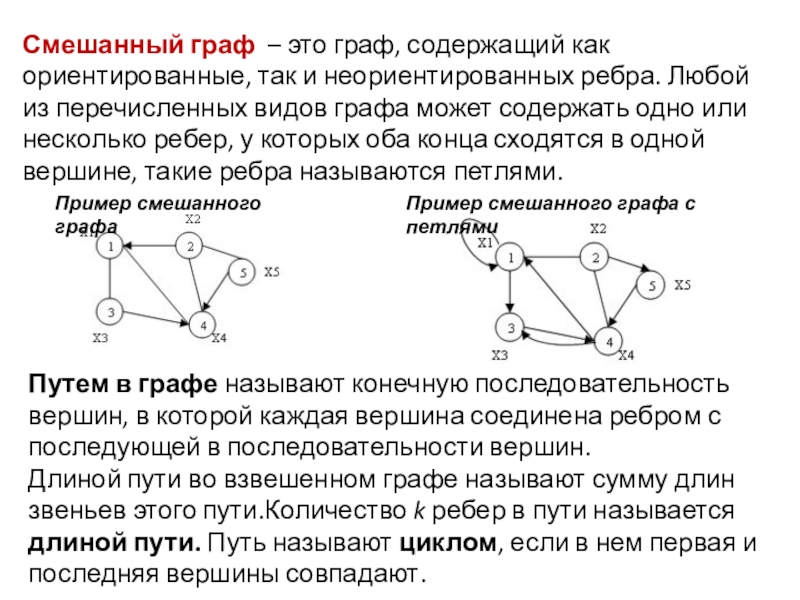
Слайд 3Смешанный граф – это граф, содержащий как ориентированные, так и неориентированных ребра. Любой
Путем в графе называют конечную последовательность вершин, в которой каждая вершина соединена ребром с последующей в последовательности вершин.
Длиной пути во взвешенном графе называют сумму длин звеньев этого пути.Количество k ребер в пути называется длиной пути. Путь называют циклом, если в нем первая и последняя вершины совпадают.
Слайд 412
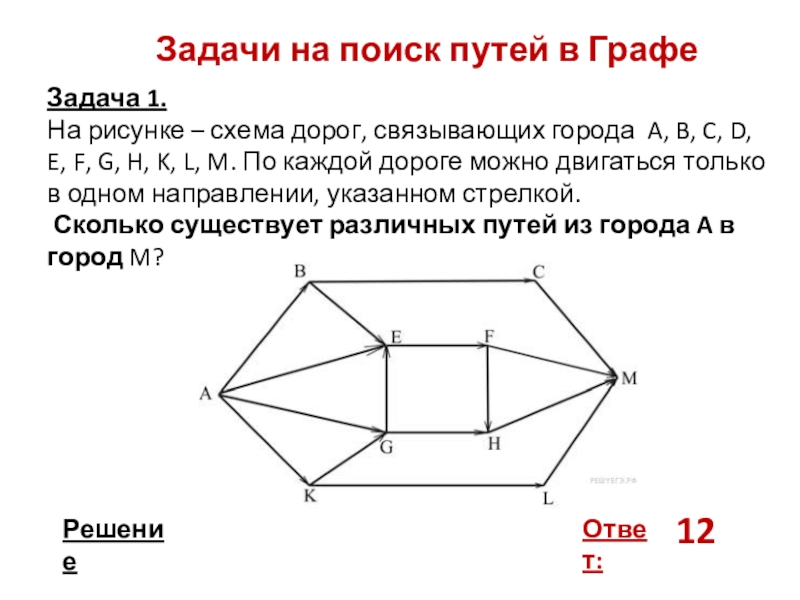
Задачи на поиск путей в Графе
Задача 1.
На рисунке – схема дорог,
Сколько существует различных путей из города A в город M?
Ответ:
12
Решение
Слайд 6Задача 2.
На рисунке – схема дорог, связывающих города А, Б, В,
Сколько существует различных путей из города
А в город И?
Ответ:
16
Решение
Слайд 7Решение задачи 2.
Начнем считать количество путей с конца маршрута – с
Аналогично:
NД = NБ;
NЖ = NБ + NВ + NЕ;
NЗ = NЖ + NЕ.
Добавим еще вершины:
NБ = NА = 1;
NВ = NА + NГ = 1 + 1 = 2;
NЕ = NВ + NГ = 2 + 1 = 3;
NГ = NА = 1.
Преобразуем первые вершины с учетом значений вторых:
NД = NБ = 1;
NЖ = NБ + NВ + NЕ = 1 + 2 + 3 = 6; NЗ = NЖ + NЕ = 6 + 3 = 9.
Подставим в формулу (1): N = NК = 1 + 6 + 9 = 16. Ответ: 16
Слайд 8Задача 3.
На рисунке изображена схема дорог, связывающих города A, B, C,
Сколько существует различных путей из города
A в город M?
Ответ:
Решение
36.
Слайд 9Решение задачи 3.
1. Начнем считать количество путей с конца маршрута —
2.Аналогично:
NL = NF+ NG = 5 + 5 = 10;
NG = NF = 5;
NH = NF = 5;
NK = NF + NE + NH = 5 + 1 + 5 = 11;
NF = NA + NB + NC + ND + NE = = 5.
3. Добавим еще вершины:
NB = NA = 1;
NC = NA = 1;
ND = NA = 1;
NE = NA = 1.
4. Подставим в формулу (*):
N = NM = 10 + 5 + 5 + 11 + 5 = 36. Ответ: 36.