- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мультимедийна презентация по информатике на тему Работа в Excel 2007, Диаграммы
Содержание
- 1. Мультимедийна презентация по информатике на тему Работа в Excel 2007, Диаграммы
- 2. диаграммы строятся на основе данных таблицыпроще всего
- 3. Основные типы диаграммГистограмма (столбчатая диаграмма): сравнение значений
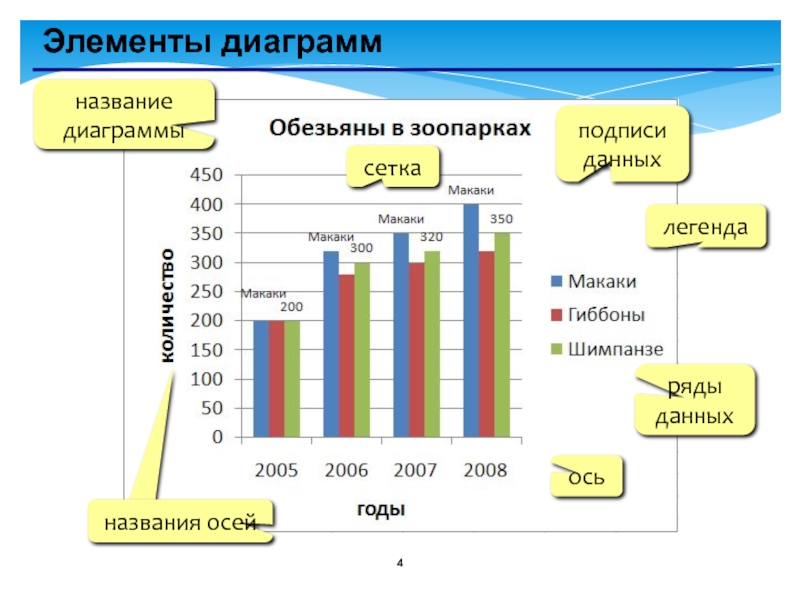
- 4. Элементы диаграммназвание диаграммылегендаряды данныхосьсеткаподписи данных
- 5. Настройка диаграммы и ее элементовКонструктор: общие свойстваМакет: настройка свойств отдельных элементовФормат: оформление отдельных элементов
- 6. Графики функцийЗадача: построить график функции
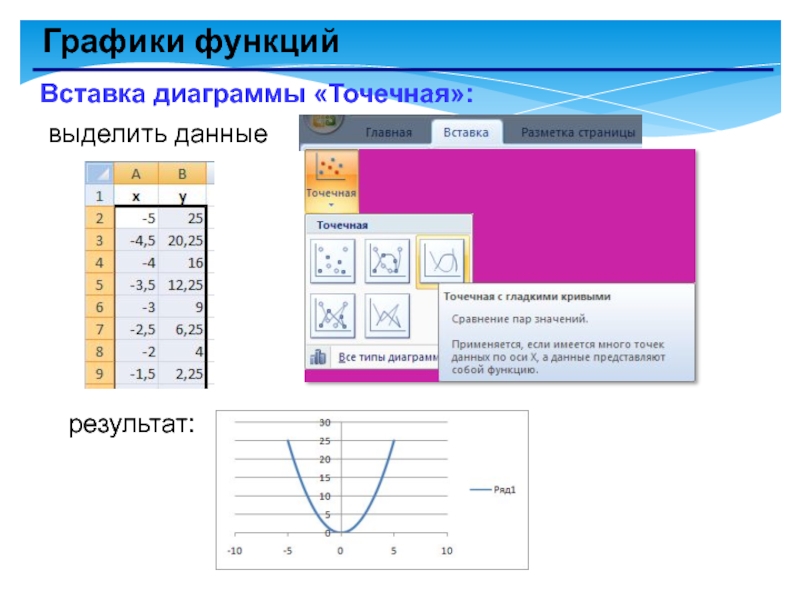
- 7. Графики функцийВставка диаграммы «Точечная»: выделить данные результат:
- 8. Работа в Excel 2007Тема 3. Численные методы© К.Ю. Поляков, 2009-2012
- 9. Решение уравненийЗадача: найти все решения уравнения
- 10. Решение уравнения1. Таблица значений функций на интервале [-5,5]2. Графики функций (диаграмма «Точечная»)2 решения: начальные приближения
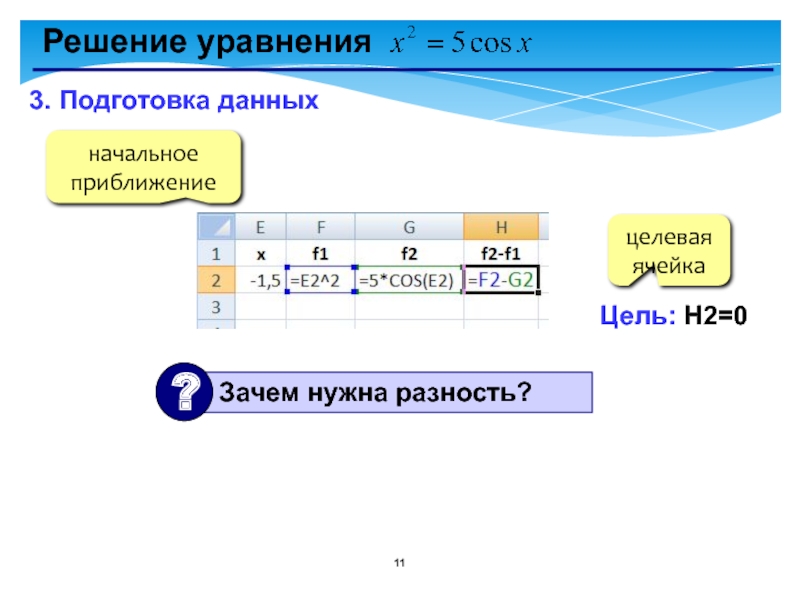
- 11. Решение уравнения 3. Подготовка данныхначальное приближениецелевая ячейкаЦель: H2=0
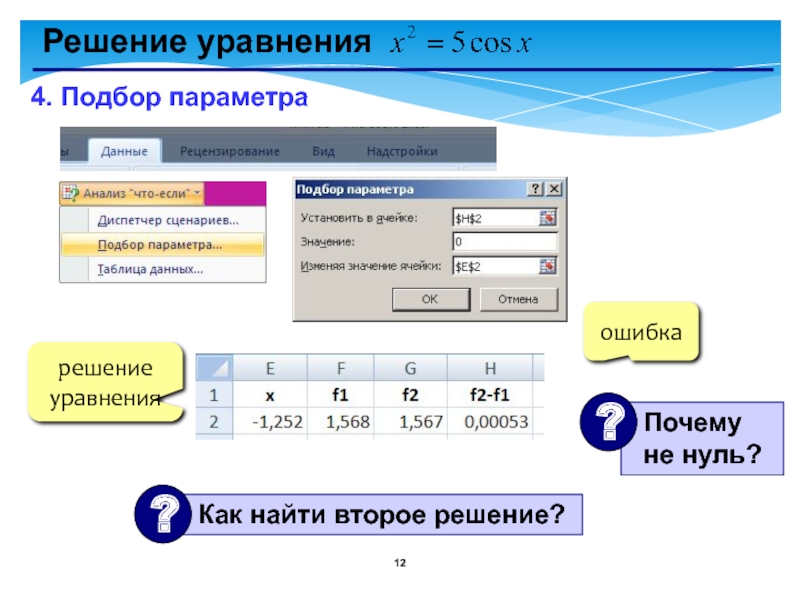
- 12. Решение уравнения 4. Подбор параметраошибкарешение уравнения
- 13. ОптимизацияОптимизация – это поиск оптимального (наилучшего) варианта
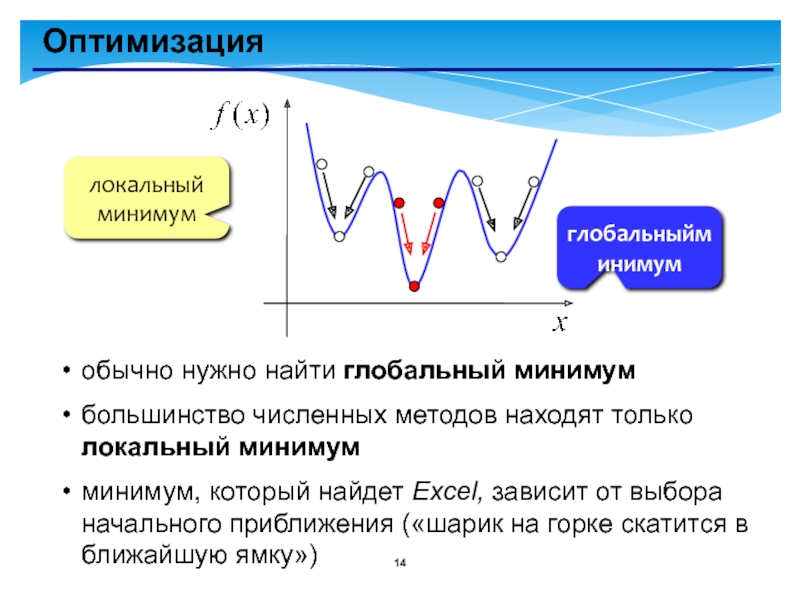
- 14. Оптимизациялокальный минимумглобальныйминимумобычно нужно найти глобальный минимумбольшинство численных
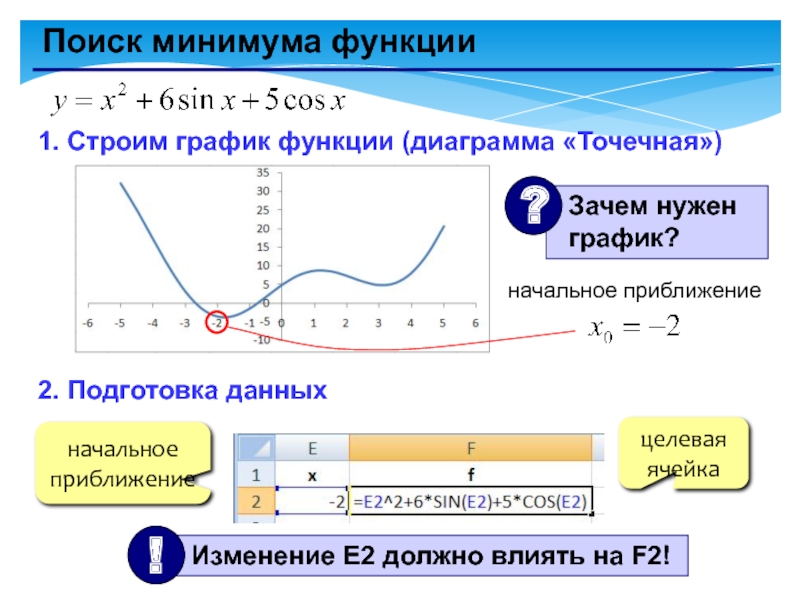
- 15. Поиск минимума функции1. Строим график функции (диаграмма «Точечная»)2. Подготовка данныхначальное приближениеначальное приближениецелеваяячейка
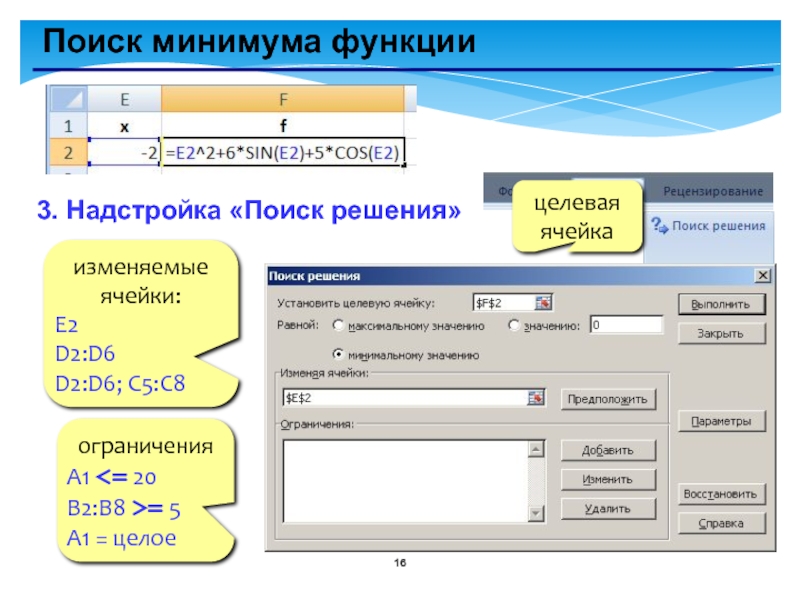
- 16. Поиск минимума функции3. Надстройка «Поиск решения»изменяемые ячейки:E2D2:D6D2:D6; C5:C8целеваяячейкаограниченияA1 = 5A1 = целое
- 17. Параметры оптимизации
- 18. ОптимизацияНадстройка «Поиск решения» позволяет:искать минимум и максимум
- 19. Работа в Excel 2007Тема 4. Статистика© К.Ю. Поляков, 2009-2012
- 20. Ряд данных и его свойстваРяд данных –
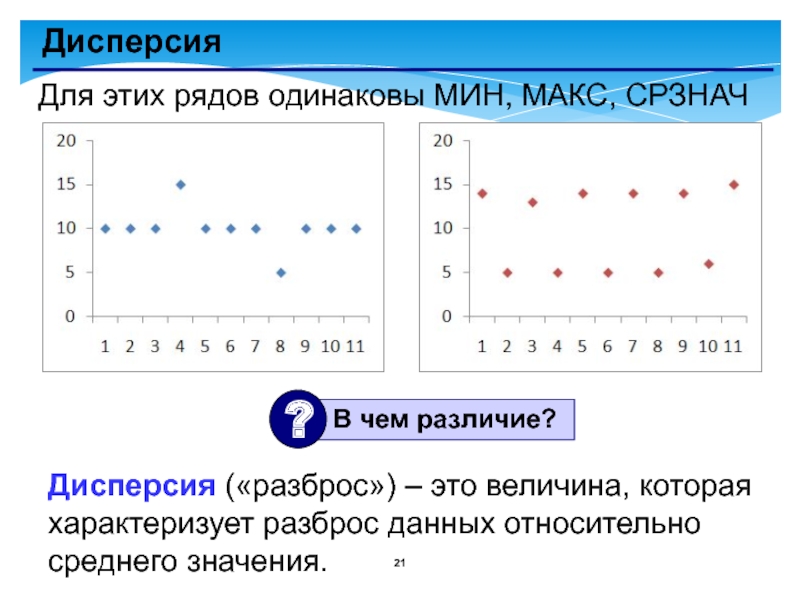
- 21. ДисперсияДля этих рядов одинаковы МИН, МАКС, СРЗНАЧДисперсия
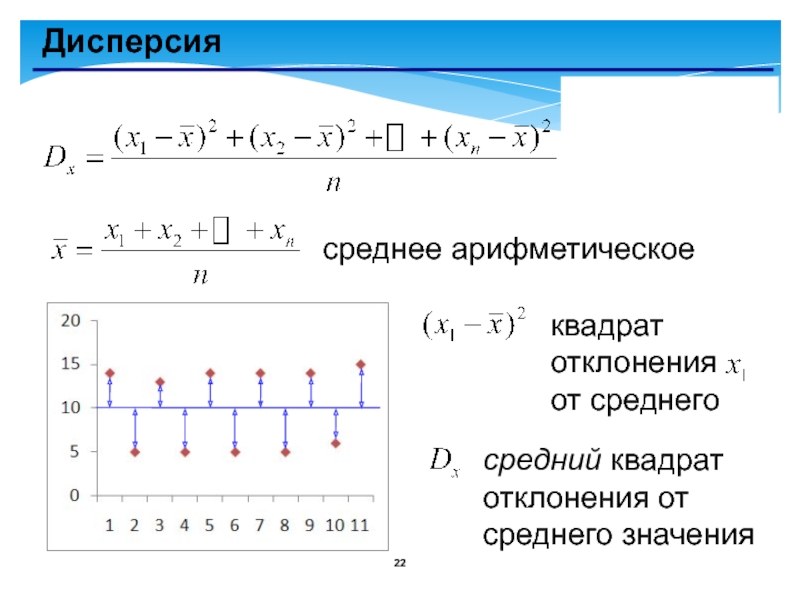
- 22. Дисперсиясреднее арифметическоеквадрат отклонения от среднегосредний квадрат отклонения от среднего значения
- 23. Дисперсия и СКВОСтандартная функция =ДИСПР(A1:A20)Что неудобно:если
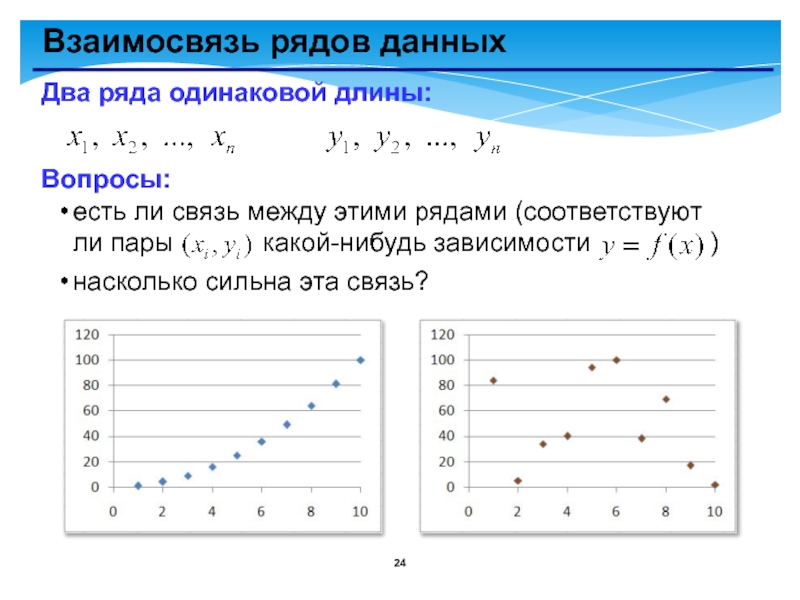
- 24. Взаимосвязь рядов данныхДва ряда одинаковой длины:Вопросы:есть ли
- 25. Взаимосвязь рядов данныхКовариация:Как понимать это число?если если
- 26. Взаимосвязь рядов данныхКоэффициент корреляции:– СКВО рядов
- 27. Взаимосвязь рядов данныхКак понимать коэффициент корреляции?
- 28. Работа в Excel 2007Тема 5. Восстановление зависимостей© К.Ю. Поляков, 2009-2012
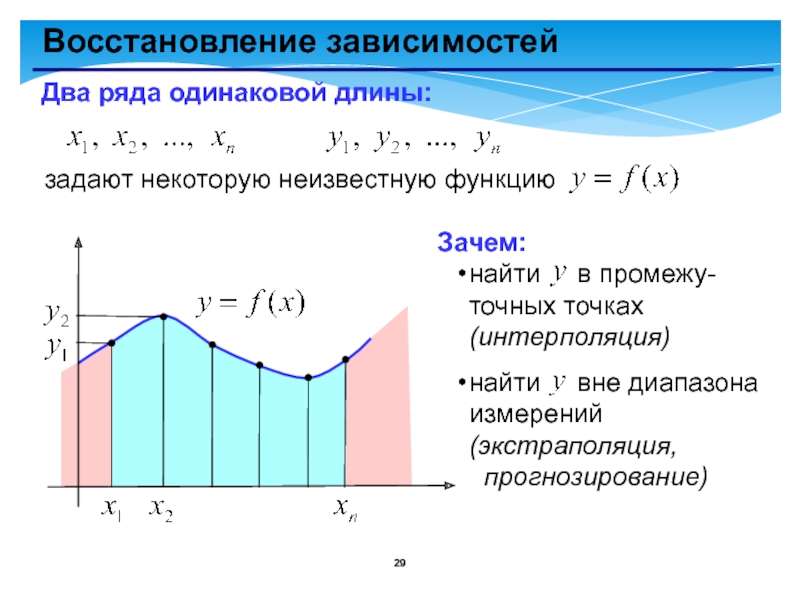
- 29. Восстановление зависимостейДва ряда одинаковой длины:задают некоторую неизвестную
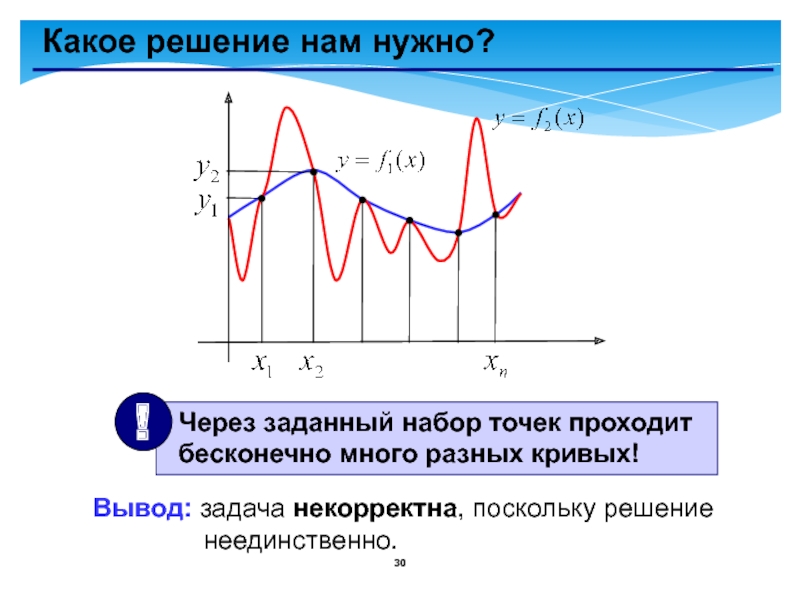
- 30. Какое решение нам нужно?Вывод: задача некорректна, поскольку
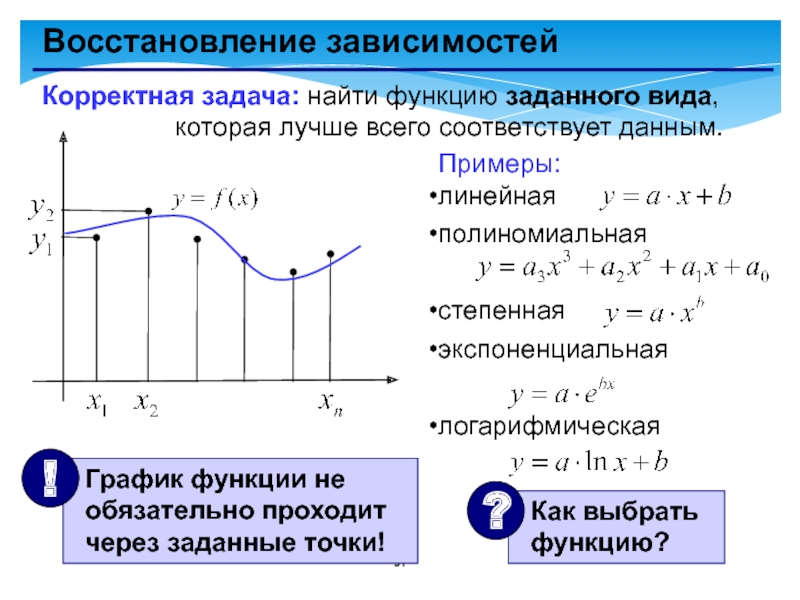
- 31. Восстановление зависимостейКорректная задача: найти функцию заданного вида,
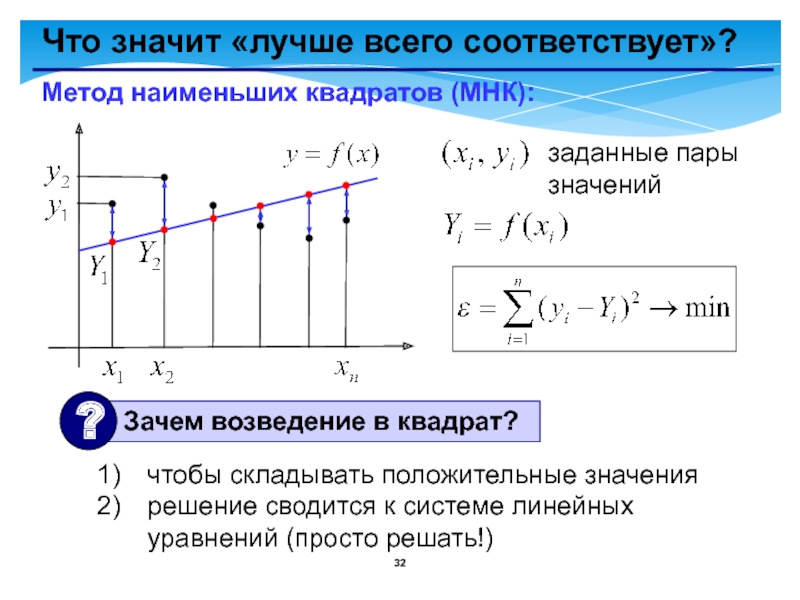
- 32. Что значит «лучше всего соответствует»?заданные пары значенийМетод
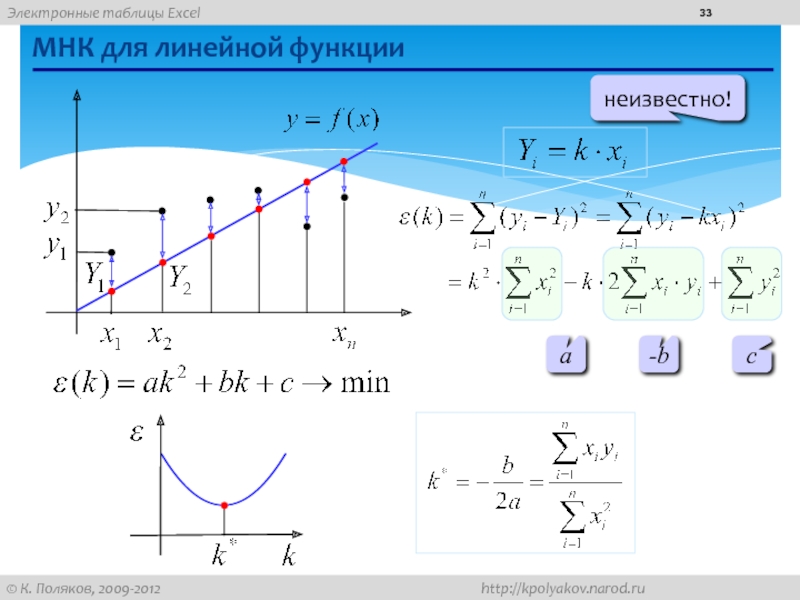
- 33. МНК для линейной функциинеизвестно!a-bc
- 34. Коэффициент достоверностизаданные пары значенийКрайние случаи:если график проходит
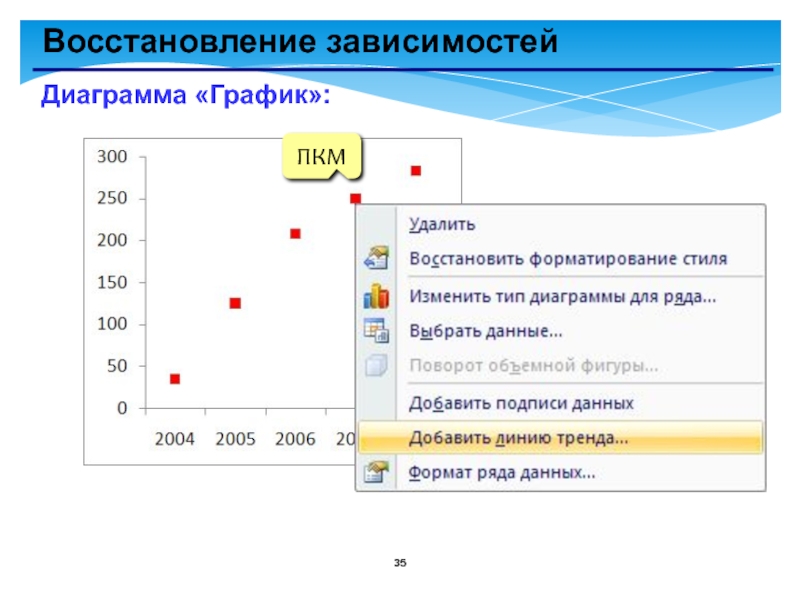
- 35. Восстановление зависимостей Диаграмма «График»: ПКМ
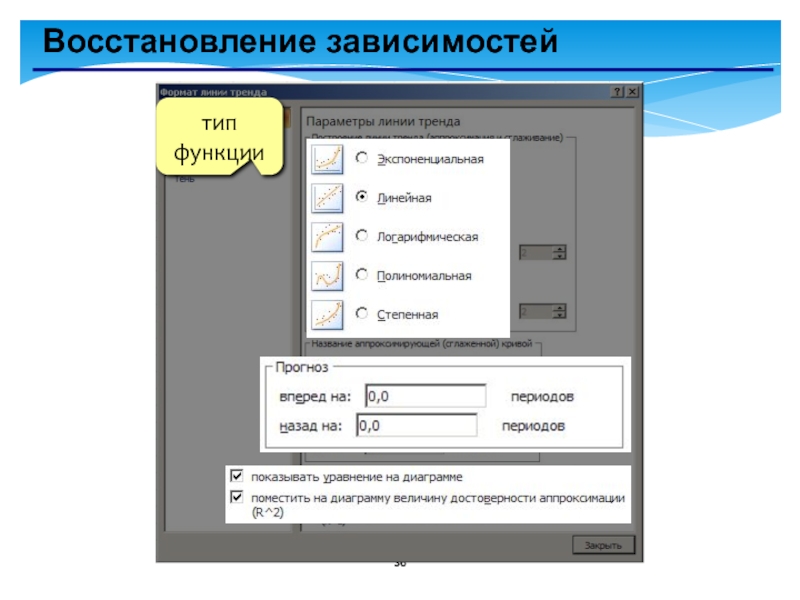
- 36. Восстановление зависимостей
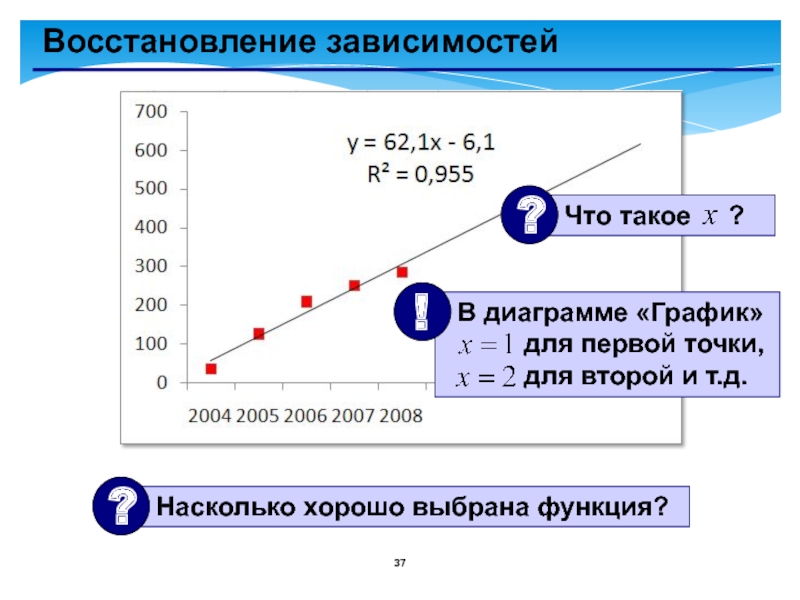
- 37. Восстановление зависимостей
- 38. Восстановление зависимостейСложные случаи (нестандартная функция):Алгоритм:выделить ячейки для
диаграммы строятся на основе данных таблицыпроще всего сначала выделить все нужные данные, а потом…все данные, которые должны обновляться автоматически, нужно выделитьдля выделения несвязанных диапазонов используем +CtrlОбщий подход
Слайд 2диаграммы строятся на основе данных таблицы
проще всего сначала выделить все нужные
данные, а потом…
все данные, которые должны обновляться автоматически, нужно выделить
для выделения несвязанных диапазонов используем +Ctrl
все данные, которые должны обновляться автоматически, нужно выделить
для выделения несвязанных диапазонов используем +Ctrl
Общий подход
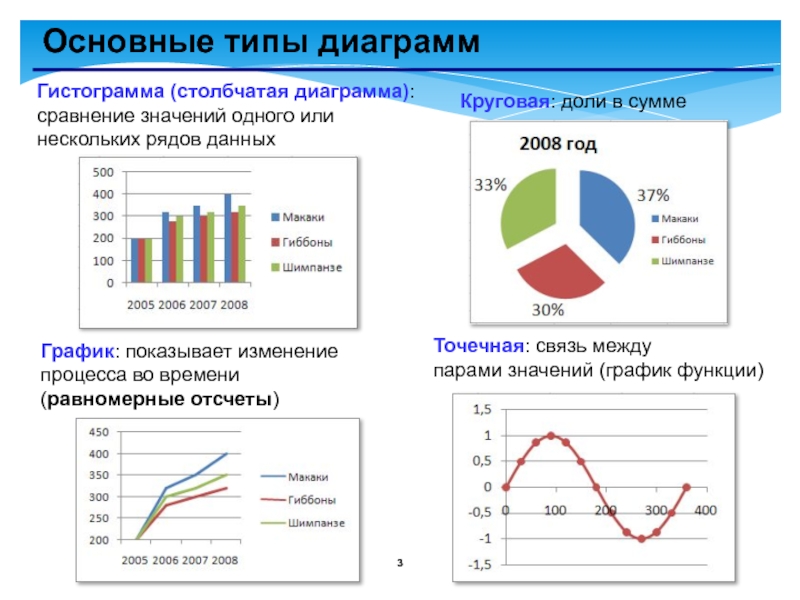
Слайд 3Основные типы диаграмм
Гистограмма (столбчатая диаграмма): сравнение значений одного или нескольких рядов
данных
График: показывает изменение процесса во времени (равномерные отсчеты)
Круговая: доли в сумме
Точечная: связь между
парами значений (график функции)
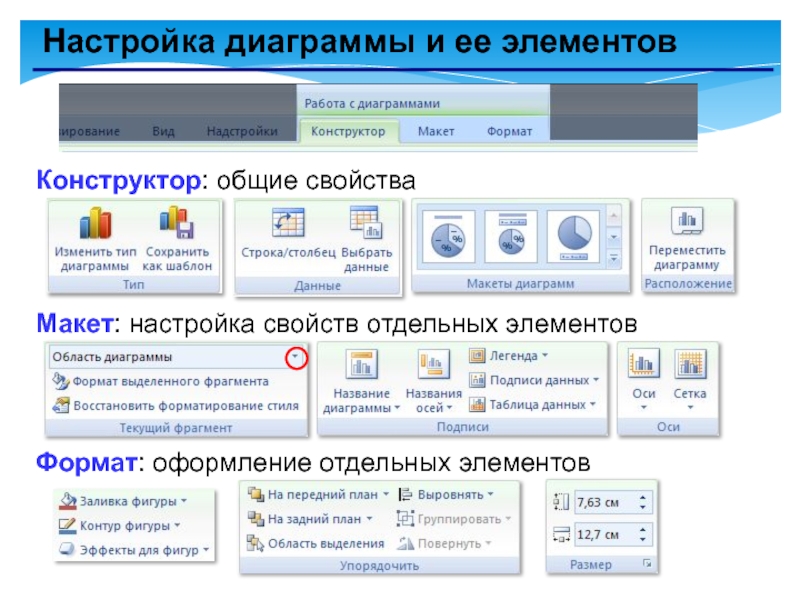
Слайд 5Настройка диаграммы и ее элементов
Конструктор: общие свойства
Макет: настройка свойств отдельных элементов
Формат:
оформление отдельных элементов
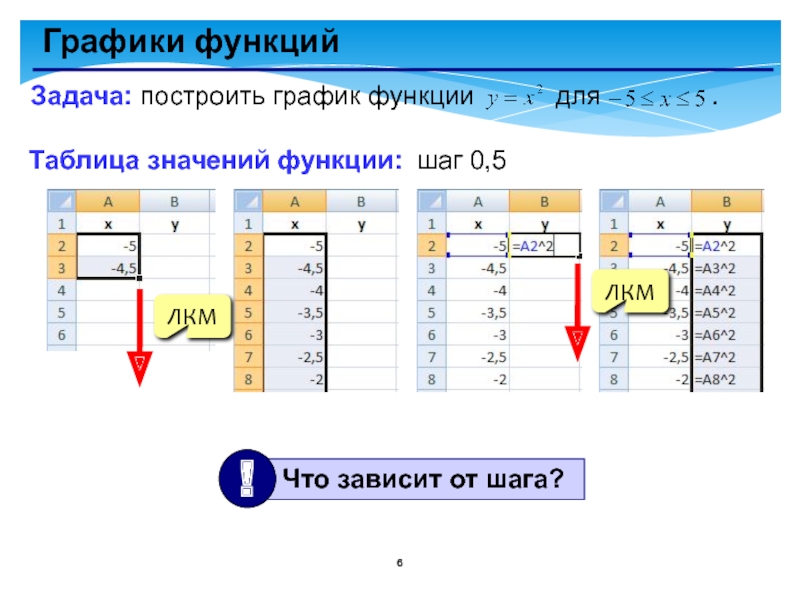
Слайд 6Графики функций
Задача: построить график функции для
.
Таблица значений функции:
шаг 0,5
ЛКМ
ЛКМ
Слайд 9Решение уравнений
Задача: найти все решения уравнения
на интервале [-5,5]
Методы решения уравнений:
аналитические: решение в виде формулы
численные: приближенное решение, число
выбрать начальное приближение «рядом» с решением
по некоторому алгоритму вычисляют первое приближение, затем – второе и т.д.
вычисления прекращают, когда значение меняется очень мало (метод сходится)
Слайд 10Решение уравнения
1. Таблица значений функций на интервале [-5,5]
2. Графики функций (диаграмма
«Точечная»)
2 решения:
начальные приближения
![Решение уравнения1. Таблица значений функций на интервале [-5,5]2. Графики функций (диаграмма «Точечная»)2 решения: начальные приближения](/img/thumbs/a730456b19be013195819b73646c2b4b-800x.jpg "Мультимедийна презентация по информатике на тему Работа в Excel 2007, Диаграммы Решение уравнения1. Таблица значений функций на интервале [-5,5]2. Графики функций (диаграмма «Точечная»)2 решения: начальные приближения")
Слайд 13Оптимизация
Оптимизация – это поиск оптимального (наилучшего) варианта в заданных условиях.
Оптимальное решение
– такое, при котором некоторая заданная функция (целевая функция) достигает минимума или максимума.
Постановка задачи:
целевая функция
ограничения, которые делают задачу осмысленной
(расходы, потери, ошибки)
(доходы, приобретения)
Задача без ограничений: построить дом
при минимальных затратах.
Решение: не строить дом вообще.
Слайд 14Оптимизация
локальный минимум
глобальныйминимум
обычно нужно найти глобальный минимум
большинство численных методов находят только локальный
минимум
минимум, который найдет Excel, зависит от выбора начального приближения («шарик на горке скатится в ближайшую ямку»)
минимум, который найдет Excel, зависит от выбора начального приближения («шарик на горке скатится в ближайшую ямку»)
Слайд 15Поиск минимума функции
1. Строим график функции (диаграмма «Точечная»)
2. Подготовка данных
начальное приближение
начальное
приближение
целевая
ячейка
Слайд 16Поиск минимума функции
3. Надстройка «Поиск решения»
изменяемые ячейки:
E2
D2:D6
D2:D6; C5:C8
целевая
ячейка
ограничения
A1 =
5
A1 = целое
A1 = целое
Слайд 18Оптимизация
Надстройка «Поиск решения» позволяет:
искать минимум и максимум функции
использовать несколько изменяемых ячеек
и диапазонов
вводить ограничения (<=, >=, целое, двоичное)
вводить ограничения (<=, >=, целое, двоичное)
Слайд 20Ряд данных и его свойства
Ряд данных – это упорядоченный набор значений
Основные
свойства (ряд A1:A20):
количество элементов =СЧЕТ(A1:A20)
количество элементов, удовлетворяющих некоторому условию: = СЧЕТЕСЛИ(A1:A20;"<5")
минимальное значение =МИН(A1:A20)
максимальное значение =МАКС(A1:A20)
сумма элементов =СУММ(A1:A20)
среднее значение =СРЗНАЧ(A1:A20)
количество элементов =СЧЕТ(A1:A20)
количество элементов, удовлетворяющих некоторому условию: = СЧЕТЕСЛИ(A1:A20;"<5")
минимальное значение =МИН(A1:A20)
максимальное значение =МАКС(A1:A20)
сумма элементов =СУММ(A1:A20)
среднее значение =СРЗНАЧ(A1:A20)
Слайд 21Дисперсия
Для этих рядов одинаковы МИН, МАКС, СРЗНАЧ
Дисперсия («разброс») – это величина,
которая характеризует разброс данных относительно среднего значения.
Слайд 22Дисперсия
среднее арифметическое
квадрат отклонения от среднего
средний квадрат отклонения от среднего значения
Слайд 23Дисперсия и СКВО
Стандартная функция
=ДИСПР(A1:A20)
Что неудобно:
если измеряется в метрах,
то – в м2
Функции – Другие – Статистические
СКВО = среднеквадратическое отклонение
=СТАНДОТКЛОНП(A1:A20)
Слайд 24Взаимосвязь рядов данных
Два ряда одинаковой длины:
Вопросы:
есть ли связь между этими рядами
(соответствуют ли пары какой-нибудь зависимости )
насколько сильна эта связь?
насколько сильна эта связь?
Слайд 25Взаимосвязь рядов данных
Ковариация:
Как понимать это число?
если
если
если
увеличение
приводит к увеличению
в среднем!
увеличение приводит к уменьшению
связь обнаружить не удалось
Что плохо?
единицы измерения: если в метрах, в литрах,
то – в м⋅л
зависит от абсолютных значений и , поэтому ничего не говорит о том, насколько сильна связь
Слайд 26Взаимосвязь рядов данных
Коэффициент корреляции:
– СКВО рядов и
безразмерный!
Как
понимать это число?
если : увеличение приводит к увеличению
если : увеличение приводит к уменьшению
если : связь обнаружить не удалось
если : увеличение приводит к увеличению
если : увеличение приводит к уменьшению
если : связь обнаружить не удалось
=КОРРЕЛ(A1:A20;B1:B20)
Слайд 27Взаимосвязь рядов данных
Как понимать коэффициент корреляции?
: очень слабая корреляция
: слабая
: средняя
: сильная
: очень сильная
: линейная зависимость
: линейная зависимость
: слабая
: средняя
: сильная
: очень сильная
: линейная зависимость
: линейная зависимость
Слайд 29
Восстановление зависимостей
Два ряда одинаковой длины:
задают некоторую неизвестную функцию
Зачем:
найти
в промежу-точных точках
(интерполяция)
найти вне диапазона измерений (экстраполяция, прогнозирование)
найти вне диапазона измерений (экстраполяция, прогнозирование)
Слайд 31Восстановление зависимостей
Корректная задача: найти функцию заданного вида,
которая лучше всего соответствует данным.
Примеры:
линейная
полиномиальная
степенная
экспоненциальная
логарифмическая
Слайд 32Что значит «лучше всего соответствует»?
заданные пары значений
Метод наименьших квадратов (МНК):
чтобы складывать
положительные значения
решение сводится к системе линейных уравнений (просто решать!)
решение сводится к системе линейных уравнений (просто решать!)
Слайд 34Коэффициент достоверности
заданные пары значений
Крайние случаи:
если график проходит через точки:
если считаем, что
y не меняется и :
– среднее значение
Слайд 38Восстановление зависимостей
Сложные случаи (нестандартная функция):
Алгоритм:
выделить ячейки для хранения
построить ряд
для тех же
построить на одной диаграмме ряды и
попытаться подобрать так, чтобы два графика были близки
вычислить в отдельной ячейке
функции: СУММКВРАЗН – сумма квадратов разностей рядов ДИСПР – дисперсия
Поиск решения:
построить на одной диаграмме ряды и
попытаться подобрать так, чтобы два графика были близки
вычислить в отдельной ячейке
функции: СУММКВРАЗН – сумма квадратов разностей рядов ДИСПР – дисперсия
Поиск решения:
