- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Математические основы вычислительной техники (8 класс)
Содержание
- 1. Математические основы вычислительной техники (8 класс)
- 2. Информация в компьютере представлена в двоичном коде, алфавит которого состоит из двух цифр (0 и 1)
- 3. Использование двоичной системы счисления в компьютерных системах
- 4. История создания двоичной системы счисления древние времена
- 5. Лейбниц Готфрид Вильгельм Gottfried Wilhelm Leibniz (1646-1716)1703
- 6. 1703 г. - Готфрид Вильгейм Лейбниц, продолжая
- 7. Джордж Буль George Boole 1815-1864Английский математик Джордж
- 8. В 1844 году Морзе Самуэль Финли Бриз
- 9. Принцип организации двоичной системы счисления В двоичной
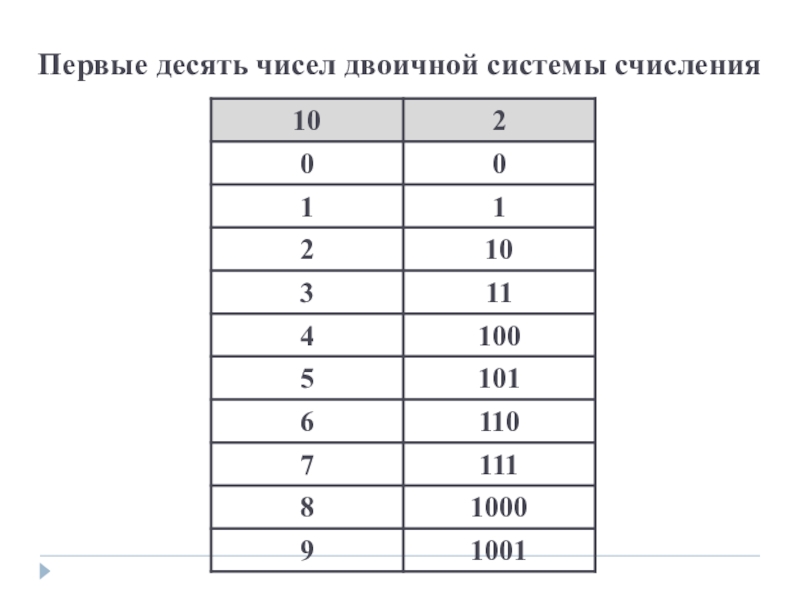
- 10. Первые десять чисел двоичной системы счисления
- 11. Двоичная запись некоторых степеней числа 10:10 =
- 12. Используя развернутую форму записи, любое число в
- 13. Перевод чисел из двоичной системы счисления в
- 14. Алгоритм перевода целых чисел из двоичной системы
- 15. Таблица степеней двойки10011012 = 26 + 23
- 16. Алгоритм перевода двоичной дроби в десятичную: целая
- 17. Алгоритм перевода целых чисел из десятичной системы
- 18. Алгоритм перевода правильной десятичной дроби в двоичную
- 19. Перевод чисел из десятичной системы счисления в
- 20. 23, 12510 → Х21) переведем целую часть:2)
- 21. Арифметические операции в двоичной системе счисленияПравила выполнения
- 22. Таблицы сложения, вычитания и умножения для двоичной
- 23. Сложение в двоичной системе счисления1 + 1
- 24. Вычитание в двоичной системе счисления112 – 10112
- 25. Умножение в двоичной системе счисленияВ двоичной системе
- 26. Деление в двоичной системе счисленияПри делении столбиком
Слайд 2Информация в компьютере представлена в двоичном коде, алфавит которого состоит из
Слайд 3Использование двоичной системы счисления в компьютерных системах связано с удобством и
Представление информации в двоичной системе счисления принято называть двоичным кодированием.
Слайд 4История создания двоичной системы счисления
древние времена – полинезийский
телеграф;
древний Китай
древняя Индия;
Европа нового времени - английская система объемных мер;
1670 г. - первая публикация о двоичной системе счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу.
Слайд 5Лейбниц Готфрид
Вильгельм
Gottfried Wilhelm Leibniz
(1646-1716)
1703 г. – опубликована статья немецкого математика Готфрида
Слайд 61703 г. - Готфрид Вильгейм Лейбниц, продолжая серию своих работ, пишет
Медаль, нарисованная Лейбницем, поясняет соотношение между двоичной и десятичной системами счисления.
Таким образом, два гения XVII века Блез Паскаль и Готфрид Лейбниц, установили первые вехи в истории развития цифровой вычислительной техники.
Слайд 7Джордж Буль
George Boole
1815-1864
Английский математик Джордж Буль опубликовал работу "Математический анализ логики".
Каждая величина в ней может принимать только одно из двух значений: истина или ложь, 1 или 0.
Слайд 8В 1844 году Морзе Самуэль Финли Бриз (1791-1872) изобрел новый телеграфный
В телеграфе в XIX-XX веках информация передавалась с помощью азбуки Морзе — в виде последовательности из точек и тире.
Слайд 9Принцип организации двоичной системы счисления
В двоичной системе счисления для записи
Основание двоичной системы равно 2.
Двоичное число представляет собой цепочку нулей и единиц.
Слайд 11Двоичная запись некоторых степеней числа 10:
10 = 10102
100 = 11001002
1000 =
10000 = 100111000100002
100000 = 110000110101000002
Существенным недостатком двоичной системы счисления является быстрый рост числа цифр в двоичном представлении.
Слайд 12Используя развернутую форму записи, любое число в двоичной системе счисления можно
10 = 10102 = 23 + 21
100 = 11001002 = 26 + 25 + 22
1000 = 11111010002 = 29 + 28 + 27 + 26 + 25 + 23
10000 = 100111000100002 = 213 + 210 + 29 + 28 + 24
Некоторые степени числа 10 в виде суммы степеней двойки:
Слайд 13Перевод чисел из двоичной системы счисления в десятичную систему счисления
Свернутая форма
Х = anan-1…a1a0 , b-1b-2…b-k
Развернутая форма записи двоичного числа Х:
Х = an*2n+an-1*2n-1+…+a1*21+a0+b-1*2-1+b-2*2-2+…+b-k*2-k+…
Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики.
Слайд 14Алгоритм перевода целых чисел
из двоичной системы счисления в десятичную:
пронумеруем цифры
сложим те степени двоек, которые соответствуют номерам цифр «1» в двоичной записи числа;
полученный результат является значением числа в десятичной системе.
1 1 0 12 = 1*23 + 1*22 + 0*21 + 1*20 = 23 + 22 + 20 = 1310
3 2 1 0
8 4 1
Слайд 15Таблица степеней двойки
10011012 = 26 + 23 + 22 + 20
6 3 2 0
111010002 = 27 + 26 + 25 + 23 = 128 + 64 + 32 + 8 = 23210
7 6 5 3
Слайд 16Алгоритм перевода двоичной дроби в десятичную:
целая часть числа переводится в
каждая цифра дробной части нумеруется слева направо, начиная с 1;
каждая цифра дробной части умножается на 2 –k , где k – номер этого числа, и результаты складываются.
1 0, 1 12 = 1*21 + 0*20 + 1*2-1 + 1*2-2 = 2+1/2+1/4 = 2,7510
1 0 -1 -2
Слайд 17Алгоритм перевода целых чисел из десятичной системы счисления в двоичную систему
12310 → Х2
Ответ: 12310 = 11110112
Каждый остаток от деления это цифра в двоичной записи числа.
Слайд 18Алгоритм перевода правильной десятичной дроби
в двоичную систему счисления:
0, 37510 → Х2
Ответ:
Слайд 19Перевод чисел из десятичной системы счисления в двоичную систему счисления
отдельно перевести дробную часть десятичного числа в двоичную систему счисления по соответствующему алгоритму;
в итоговой записи полученного числа целую часть от дробной отделить запятой.
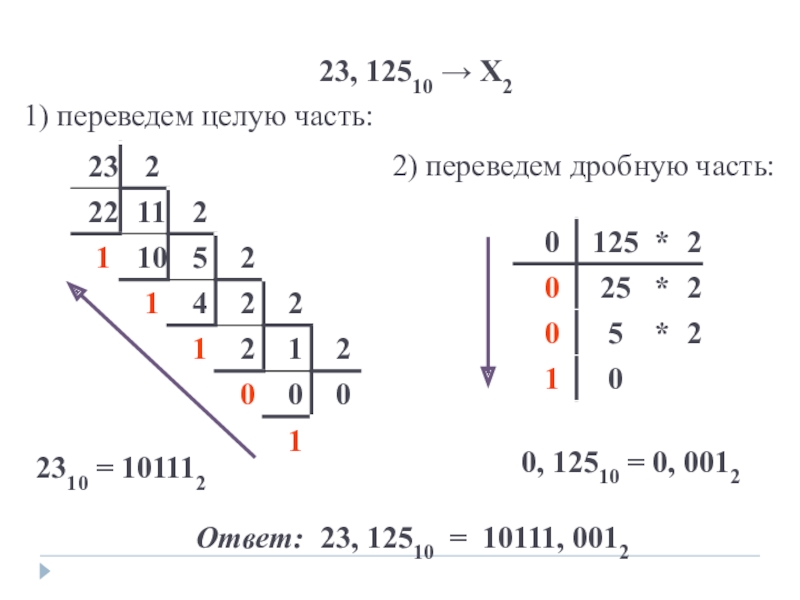
Слайд 20
23, 12510 → Х2
1) переведем целую часть:
2) переведем дробную часть:
2310 =
0, 12510 = 0, 0012
Ответ: 23, 12510 = 10111, 0012
Слайд 21Арифметические операции в двоичной системе счисления
Правила выполнения арифметических операций в позиционных
справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;
справедливы правила сложения, вычитания, умножения и деления столбиком;
правила выполнения арифметических операций опираются на таблицы сложения, вычитания и умножения Р-ичных цифр.
Слайд 22Таблицы сложения, вычитания и умножения
для двоичной системы счисления
0 + 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
10 + 1 = 11
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
10 - 1 = 1
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
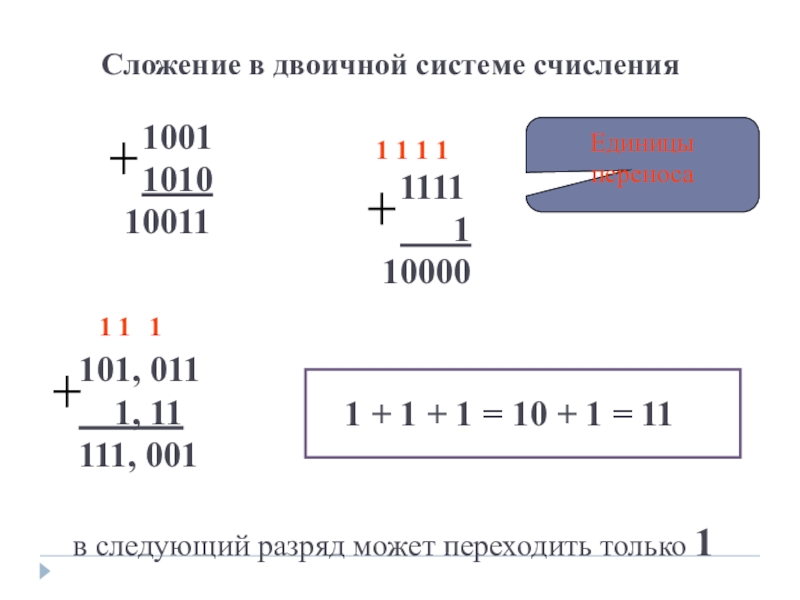
Слайд 23Сложение в двоичной системе счисления
1 + 1 + 1 = 10
в следующий разряд может переходить только 1
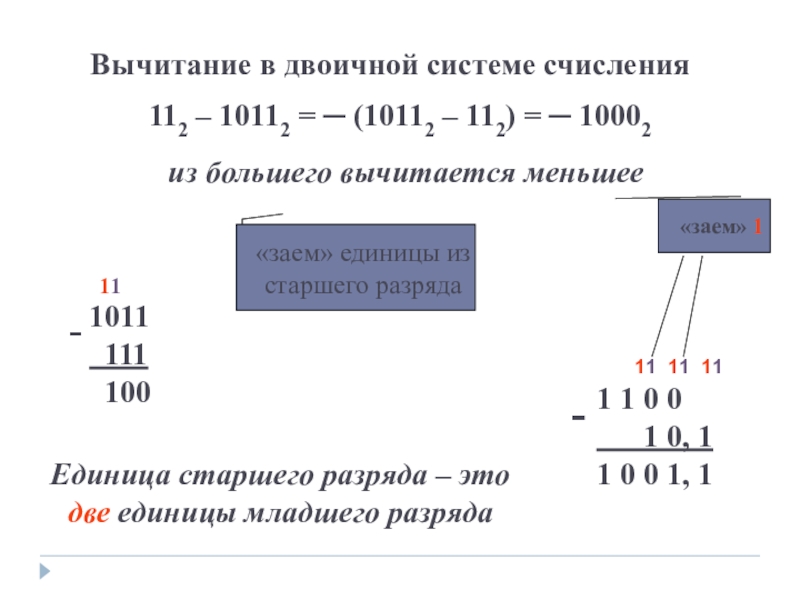
Слайд 24Вычитание в двоичной системе счисления
112 – 10112 = ─ (10112 –
из большего вычитается меньшее
Единица старшего разряда – это две единицы младшего разряда
«заем» 1
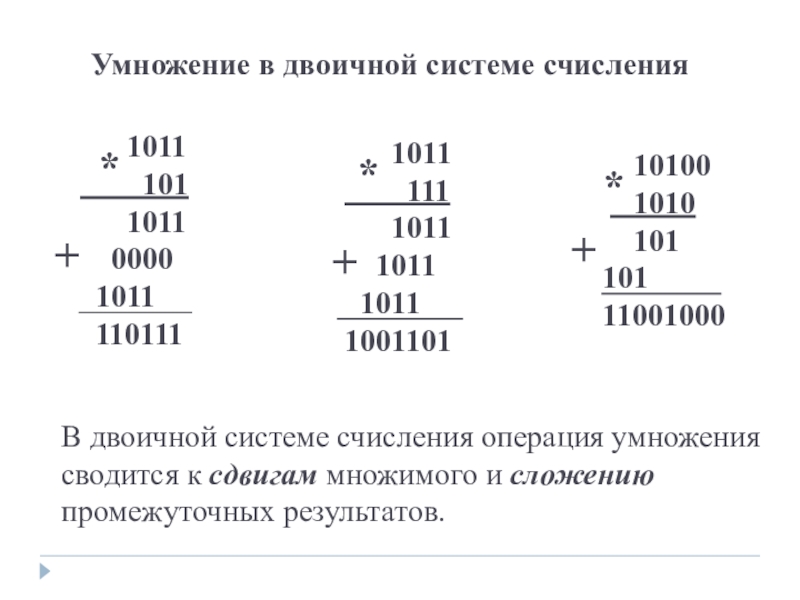
Слайд 25Умножение в двоичной системе счисления
В двоичной системе счисления операция умножения сводится
Слайд 26Деление в двоичной системе счисления
При делении столбиком в качестве промежуточных вычислений
Выполнять операцию деления можно до выделения периода или до получения требуемого количества знаков после запятой.