- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Математическая логика.Алгебра логики
Содержание
- 1. Математическая логика.Алгебра логики
- 2. ВысказываниеВысказывание – это форма мышления, в которой
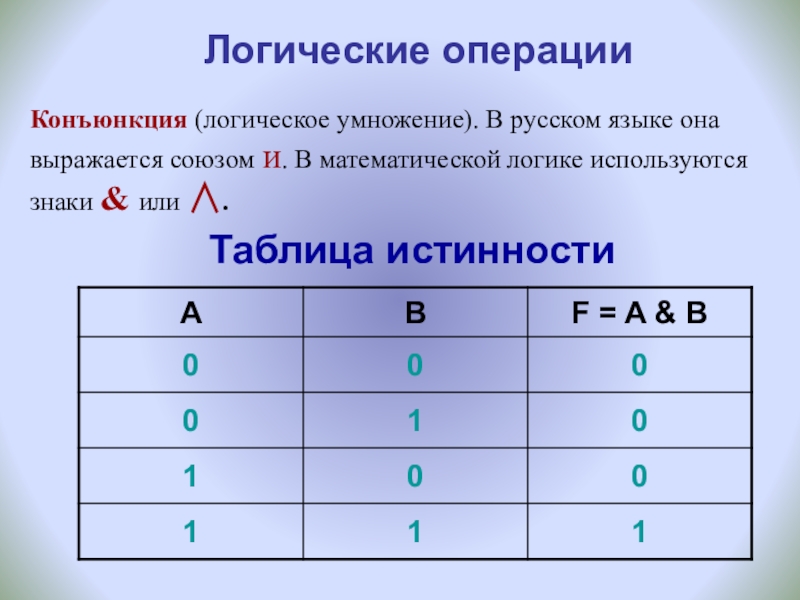
- 3. Логические операцииКонъюнкция (логическое умножение). В русском языке
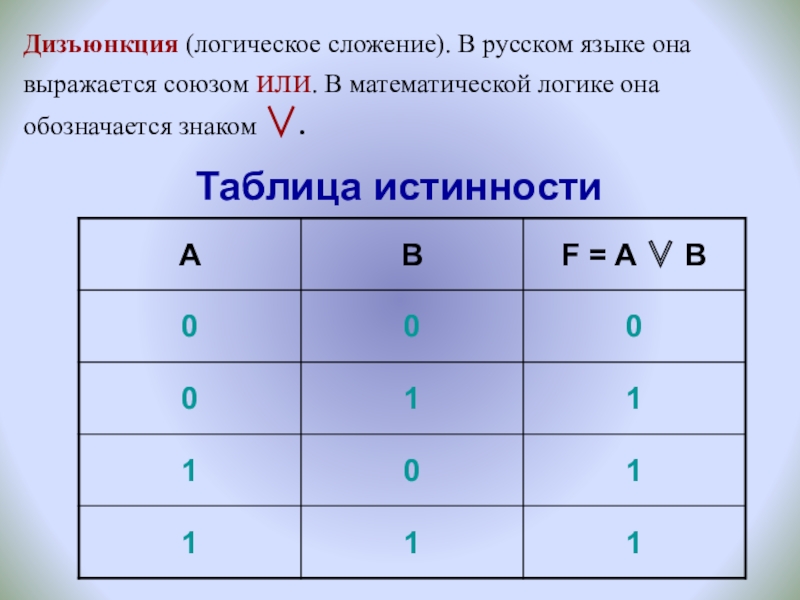
- 4. Дизъюнкция (логическое сложение). В русском языке она
- 5. Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией. Обозначение инверсии: ¬; ¯Таблица истинности
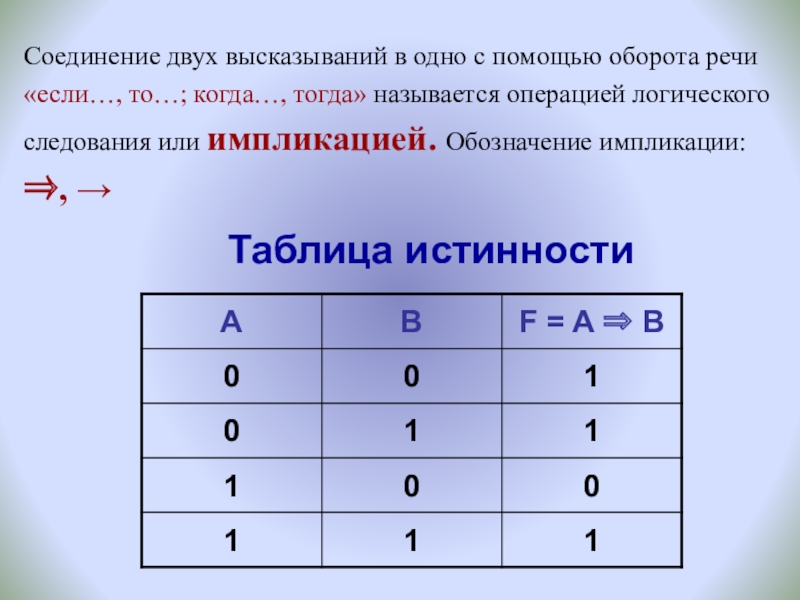
- 6. Таблица истинностиСоединение двух высказываний в одно с
- 7. Соединение двух высказываний в одно помощью оборота
- 8. Логические операции выполняются в следующем порядке: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. Скобки позволяют этот порядок изменить:
- 9. Таблицы истинности Решение логических выражений принято оформлять в
- 10. Для составления таблицы истинности необходимо:Выяснить количество строк
- 11. Задача 1:Построим таблицу истинности для функции
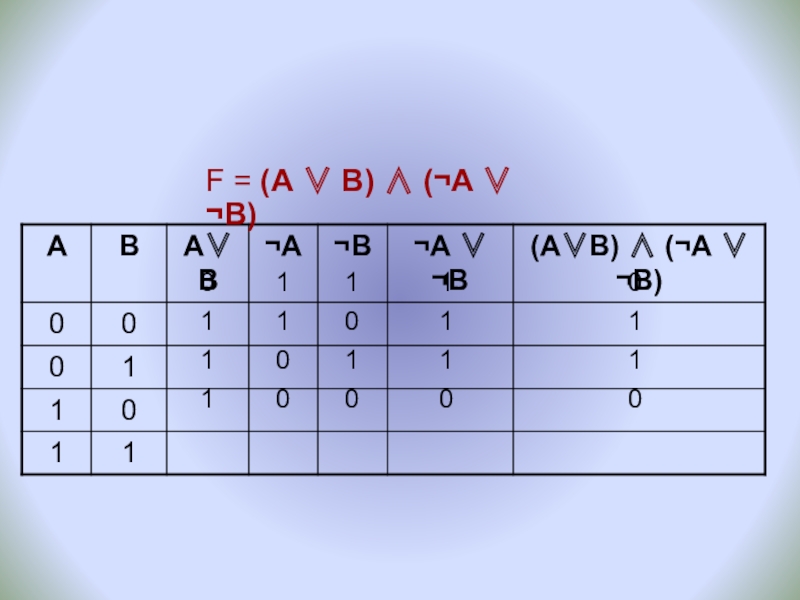
- 12. 01111100F = (А ∨ В) ∧ (¬A ∨ ¬B)101011100110
- 13. Задача 2:Построим таблицу истинности для функции
- 14. 00001111F = X ∨ Y ∧ ¬Z0011001101010101101010100010001000101111
- 15. Задача 3: Составьте таблицу истинности для функции А ∨ ¬ВA0011B0101¬B1010A ∨ ¬B1011
- 16. Задача 4: Даны значения: x =
- 17. Задача 4.1: Даны значения: x =
- 18. Задача 4.2: Даны значения: x
- 19. Задача 4.3: Даны значения: x
- 20. Задача 4.4: Даны значения: x
- 21. Задача 4.5: Даны значения: x
- 22. Логические законы
- 23. Задача 5: Упростите выражение:
- 24. Задача 6: Упростите выражение:
- 25. Задача 7: Упростите выражение:
Слайд 1Математическая логика
Алгебра логики (алгебра высказываний) - раздел математической логики, изучающий
(форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов .
Слайд 2Высказывание
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается
Высказывание может быть либо истинно, либо ложно;
Высказывания могут быть выражены с помощью естественных и формальных языков;
Высказывания могут быть выражены только повествовательным предложением;
Высказывания могут быть простыми и составными;
Истинность простых высказываний определяется на основании здравого смысла;
Истинность составных высказываний определяется с помощью алгебры высказываний.
Слайд 3
Логические операции
Конъюнкция (логическое умножение). В русском языке она выражается союзом и.
Таблица истинности
Слайд 4Дизъюнкция (логическое сложение). В русском языке она выражается союзом или. В
Таблица истинности
Слайд 5Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.
Таблица истинности
Слайд 6Таблица истинности
Соединение двух высказываний в одно с помощью оборота речи «если…,
Слайд 7Соединение двух высказываний в одно помощью оборота речи «тогда и только
Обозначение эквивалентности: ≡, ⇔,
Таблица истинности
Слайд 8Логические операции выполняются в следующем порядке: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
Слайд 9Таблицы истинности
Решение логических выражений принято оформлять в виде таблиц, в которых
Слайд 10Для составления таблицы истинности необходимо:
Выяснить количество строк (2n, где n –
Выяснить количество столбцов (количество переменных + количество логических операций)
Построить таблицу, указывая названия столбцов и возможные наборы значений переменных
Заполнить таблицу истинности по столбцам
Слайд 11Задача 1:
Построим таблицу истинности для функции
F = (А ∨ В)
Переменных: две (А и В), т.е. N = 2 ⇒ количество строк: 2n=22=4. С заголовком: 5
Количество столбцов: 2 переменные + 5 операций (∨,∧,¬,∨ и ¬). Итого 7
Порядок операций:
1 5 2 4 3
F = (А ∨ В) ∧ (¬A ∨ ¬B)
Слайд 13Задача 2:
Построим таблицу истинности для функции
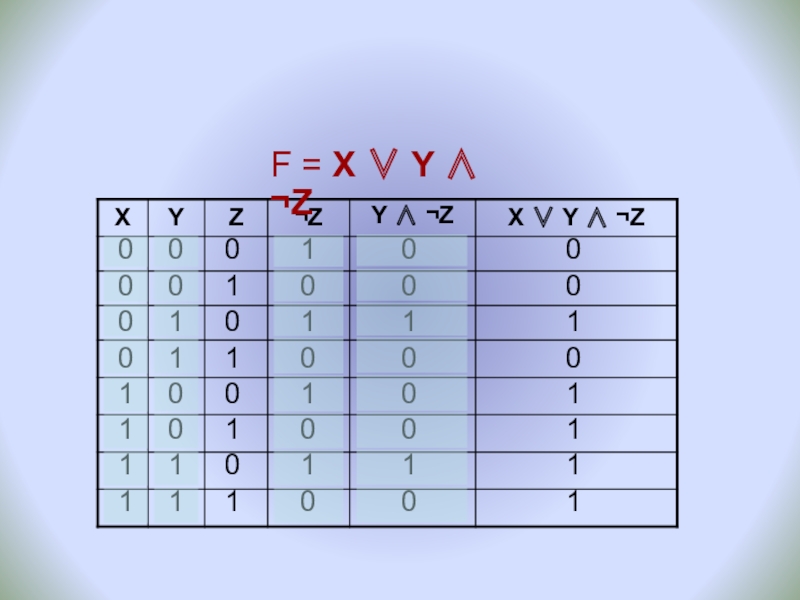
F = X ∨ Y
Переменных:
три (X, Y и Z), т.е. n = 3 ⇒ количество строк: 2n=23=8. С заголовком: 9
Количество столбцов:
3 переменные + 3 операции (∨,∧,¬). Итого 6
Порядок операций:
3 2 1
F = X ∨ Y ∧ ¬Z
Слайд 16Задача 4: Даны значения: x = 0, y = 1, z
x ∧ (y ∧ z)
(x ∧ y) ∧ z
x → (y → z)
x ∧ y → z
(x ∧ y) ⇔ (z ∨ ¬y)
Слайд 17Задача 4.1: Даны значения: x = 0, y = 1, z
x ∧ (y ∧ z)
x ∧ (1 ∧ 1)
x ∧ 1
0 ∧ 1
0 (ложь)
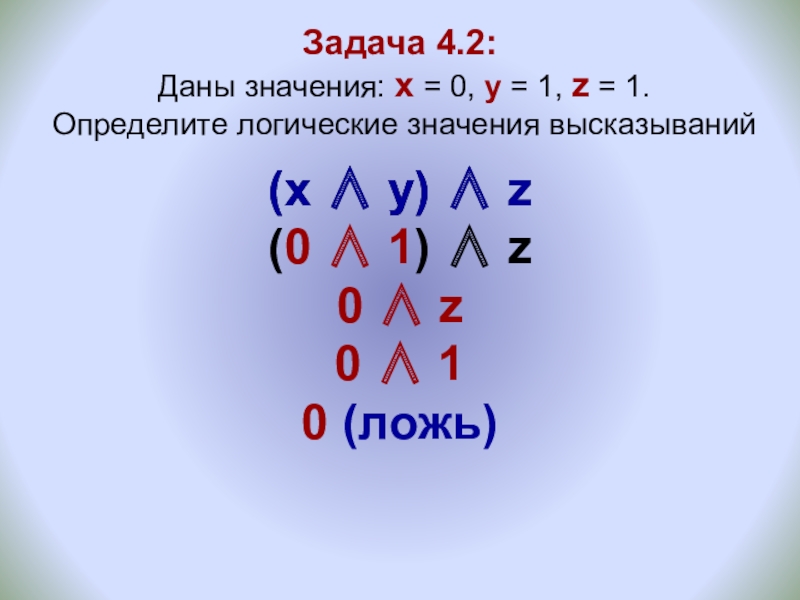
Слайд 18Задача 4.2: Даны значения: x = 0, y = 1,
(x ∧ y) ∧ z
(0 ∧ 1) ∧ z
0 ∧ z
0 ∧ 1
0 (ложь)
(x ∧ y) ∧ z
Слайд 19Задача 4.3: Даны значения: x = 0, y = 1,
x → (y → z)
x → (1 → 1)
x → 1
0 → 1
1 (истина)
x → (y → z)
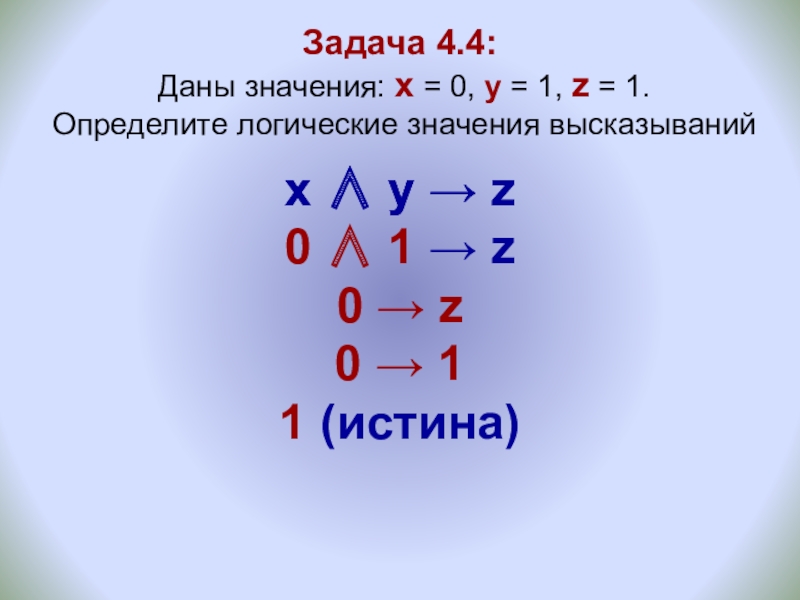
Слайд 20Задача 4.4: Даны значения: x = 0, y = 1,
x ∧ y → z
0 ∧ 1 → z
0 → z
0 → 1
1 (истина)
x ∧ y → z
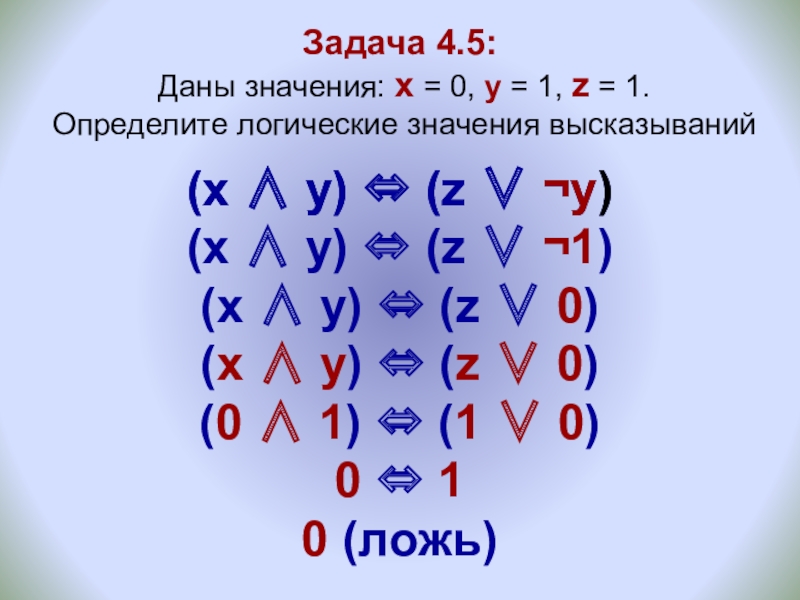
Слайд 21Задача 4.5: Даны значения: x = 0, y = 1,
(x ∧ y) ⇔ (z ∨ ¬y)
(x ∧ y) ⇔ (z ∨ ¬1)
(x ∧ y) ⇔ (z ∨ 0)
(x ∧ y) ⇔ (z ∨ 0)
(0 ∧ 1) ⇔ (1 ∨ 0)
0 ⇔ 1
0 (ложь)
(x ∧ y) ⇔ (z ∨ ¬y)
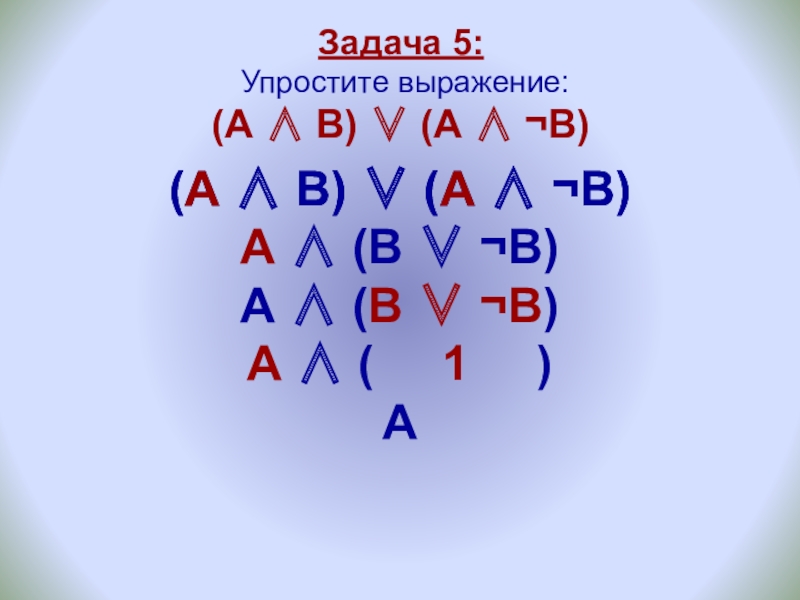
Слайд 23Задача 5: Упростите выражение: (А ∧ В) ∨ (А ∧
(А ∧ В) ∨ (А ∧ ¬В)
А ∧ (В ∨ ¬В)
А ∧ (В ∨ ¬В)
А ∧ ( 1 )
А
(А ∧ В) ∨ (А ∧ ¬В)
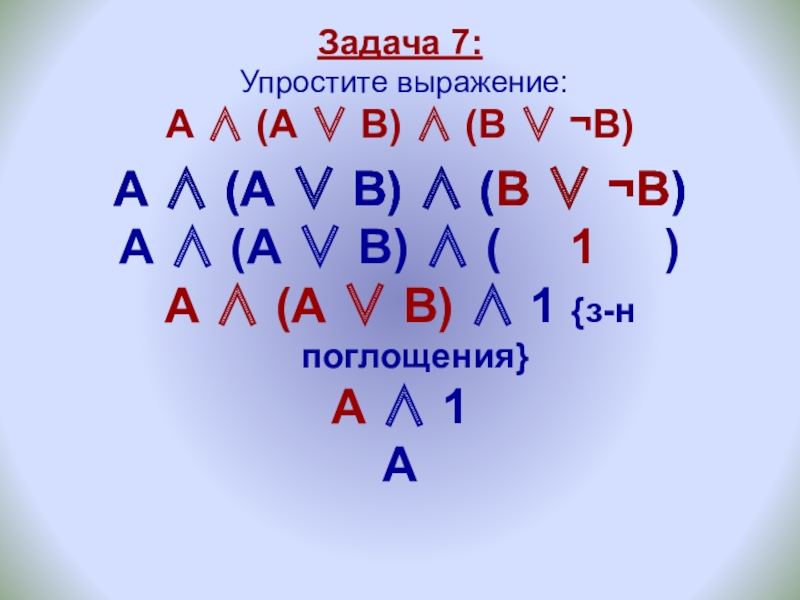
Слайд 25Задача 7: Упростите выражение: А ∧ (А ∨ В) ∧
А ∧ (А ∨ В) ∧ (В ∨ ¬В)
А ∧ (А ∨ В) ∧ ( 1 )
А ∧ (А ∨ В) ∧ 1 {з-н поглощения}
А ∧ 1
А
А ∧ (А ∨ В) ∧ (В ∨ ¬В)