- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Логические выражения и таблица истинности
Содержание
- 1. Логические выражения и таблица истинности
- 2. Таблица истинности - таблица, показывающая, какие значения
- 3. Алгоритм построения таблицы истинности:1. подсчитать количество
- 4. Заполнение таблицы:1. разделить колонку значений
- 5. Пример 1. Для формулы A/\ (B \/
- 6. Пример 2. Определите истинность логического выражения F(А,
- 7. Пример 3. Постройте таблицу истинности для логического выраженияF
- 8. Пример 4. Определите истинность формулы: F = ((С
- 9. Пример 5. Символом F обозначено одно из
- 10. Чтобы решить данную задачу можно построить часть
- 11. Рассмотрим данный конкретный пример:1) первое
Таблица истинности - таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.Логическое выражение - составные высказывания в виде формулы.Равносильные логические выражения – логические выражения, у которых последние столбцы
Слайд 2Таблица истинности - таблица, показывающая, какие значения принимает составное высказывание при
всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение - составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Логическое выражение - составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Слайд 3Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом
выражении;
2. определить число строк в таблице по формуле m=2n, где n - количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
2. определить число строк в таблице по формуле m=2n, где n - количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Слайд 4Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и
заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Слайд 5Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу
истинности.
Количество логических переменных 3, следовательно, количество строк - 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов - 3 + 5 = 8
Количество логических переменных 3, следовательно, количество строк - 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов - 3 + 5 = 8
Слайд 6Пример 2. Определите истинность логического выражения
F(А, В) = (А\/ В)/\(¬А\/¬В) .
1.
В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
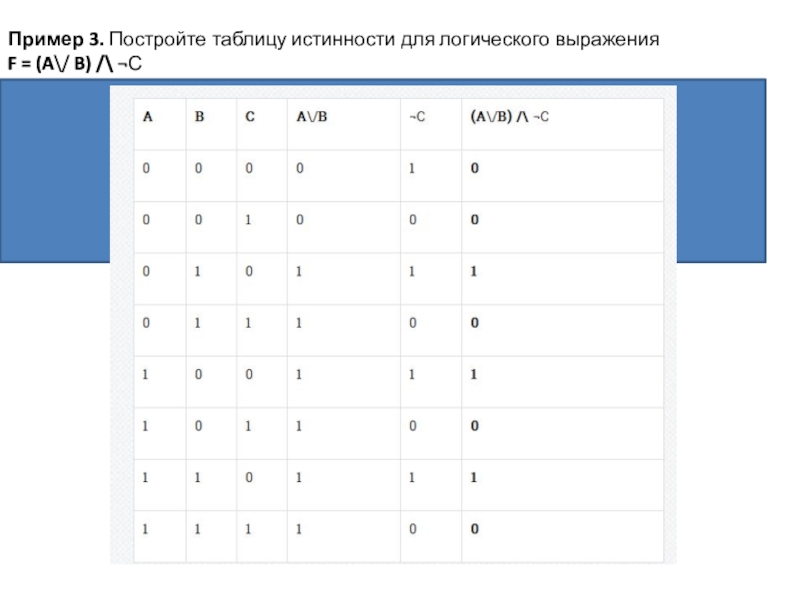
Слайд 7Пример 3. Постройте таблицу истинности для логического выражения
F = (A\/ B) /\ ¬С
В данной
функции три логические переменные – А, В, С
количество строк таблицы = 23 =8
В формуле 3 логические операции.
Расставляем порядок действий
1) А\/ В; 2) ¬С; 3) (AVB) /\ ¬С .
количество столбцов таблицы = 3 + 3 = 6
количество строк таблицы = 23 =8
В формуле 3 логические операции.
Расставляем порядок действий
1) А\/ В; 2) ¬С; 3) (AVB) /\ ¬С .
количество столбцов таблицы = 3 + 3 = 6
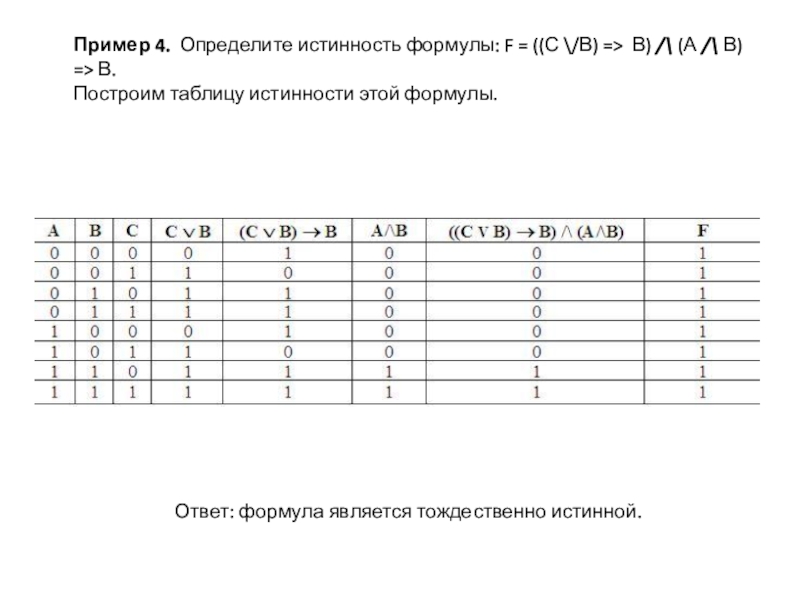
Слайд 8Пример 4. Определите истинность формулы: F = ((С \/В) => В) /\ (А /\ В) => В.
Построим
таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Слайд 9Пример 5. Символом F обозначено одно из указанных ниже логических выражений
от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Дан фрагмент таблицы истинности выражения F:
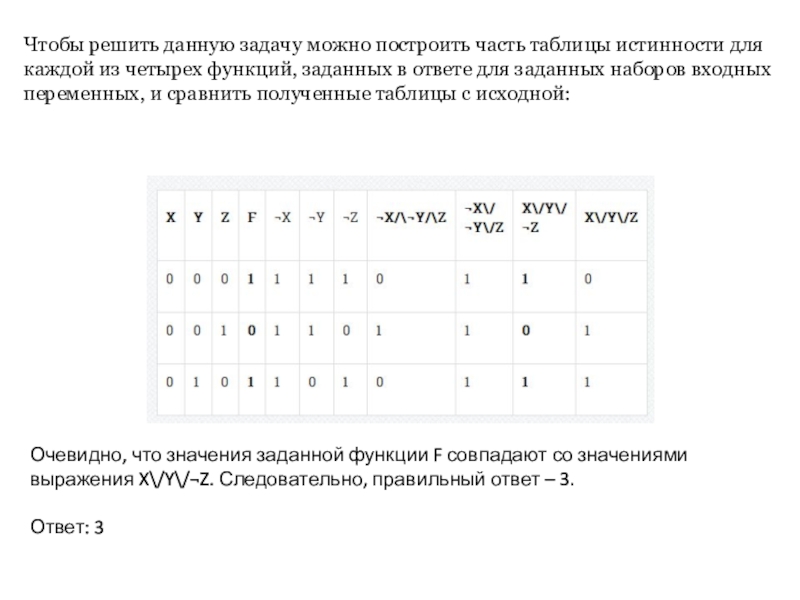
Слайд 10Чтобы решить данную задачу можно построить часть таблицы истинности для каждой
из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Слайд 11Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/\¬Y/\Z =
0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
2) второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Вариант 2