- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Логические основы персонального компьютера
Содержание
- 1. Логические основы персонального компьютера
- 2. Введение в алгебру логики «Я, по крайней
- 3. Логика – наука о законах мышления и
- 4. Алгебра логики изучает свойства функций, у
- 5. Родоначальник – Аристотель (IV век до н.
- 6. Дж. Буль (1815-1864)Отцом алгебры логики по праву
- 7. Большой вклад в становление и развитие алгебры
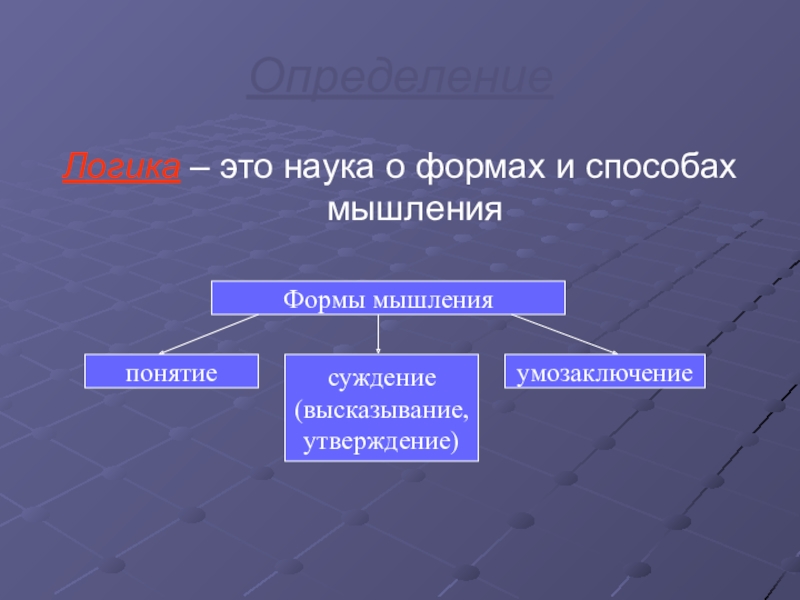
- 8. ОпределениеЛогика – это наука о формах и способах мышления
- 9. Понятие – это форма мышления, фиксирующая основные,
- 10. ВысказываниеВысказывание – это форма мышления, в которой
- 11. Об истинности высказыванийЭто не простой вопрос.
- 12. Высказывание — это языковое образование, в отношении
- 13. Не всякое предложение является логическим высказыванием.
- 14. Употребляемые в обычной речи слова и словосочетания
- 15. ВысказыванияПростыеСоставныеПолучаются из простых с использованием логических операций
- 16. "Петров — врач", "Петров — шахматист"
- 17. ВопросыСтраница 135№1Установите, какие из следующих высказываний являются
- 18. Вывод:Логическое высказывание – это любое повествовательное предложение,
- 19. Слайд 19
- 20. Алгебра логики изучает строение (форму, структуру)
- 21. Простейшие логические операцииОтрицаниеКонъюнкцияДизъюнкцияИмпликацияЭквивалентностьШтрих ШеффераСтрелка ПирсаПереход к разделу «Законы логики»
- 22. Меню выбора операцийА – лампочка горит
- 23. Конъюнкция “и” F = A · B=A
- 24. Дизъюнкция “или” (логическое сложение) F = A
- 25. Импликация “если … то” (implico – тесно
- 26. Эквивалентность (равнозначность) “тогда и только тогда” в
- 27. Меню выбора операций
- 28. Меню выбора операций
- 29. Самостоятельная работаФормализуйте следующие высказывания
- 30. Законы логикиx ≡ x закон тождестваx · x
- 31. Следствия из законов
- 32. Составление таблиц истинности по логическим формулам1-ый способ2-ой способ
- 33. Задание на домП. 5.9 Основные законы алгебры
- 34. Самостоятельная работаВАРИАНТ 1Определите, является ли указанная формула
- 35. 5.11. Как упростить логическую формулу?Под упрощением формулы,
- 36. x+y * (x*y) = x*y*x*y = x*x*y*y
- 37. Как упростить логическую формулуx*y v x*y*z v
- 38. Слайд 38
- 39. Домашнее заданиеП. 5.1114 (в,г)15(в,г)16 (а.б)Домашнее задание 2 (№3-5)
- 40. Самостоятельная работаВариант 1а) б) Вариант 2а)б)Упростите следующие
- 41. Что такое переключательная схема?Переключательная схема – это
- 42. Функции проводимости F некоторых переключательных схем:a)
- 43. Функции проводимости F некоторых переключательных схем:д) Схема
- 44. Синтез и анализ схемыСИНТЕЗ СХЕМЫ по заданным
- 45. Примеры1. Построить схему, содержащую 4 переключателя x,
- 46. Примеры2. Построим схему с пятью переключателями, которая
- 47. Примеры3. Найдем функцию проводимости схемы: Решение. Имеется
- 48. 4. Упростим переключательные схемыа) Решение: Упрощенная схема: Б)Решение: Упрощенная схема:
- 49. 4. Упростим переключательные схемыв) Решение: Упрощенная схема:
- 50. 4. Упростим переключательные схемыг) Решение: Упрощенная схема:
- 51. 4. Упростим переключательные схемыд) Решение: Упрощенная схема:
- 52. 4. Упростим переключательные схемые) Решение: Упрощенная схема:
- 53. №18б Найти F проводимости следующих переключательных схем Решение: Упрощенная схема:
- 54. №18б Найти F проводимости следующих переключательных схем Решение: Упрощенная схема:
- 55. №19a Проверьте равносильность следующий переключательных схем Решение:
- 56. Домашнее заданиеП.5.1218(в,г)19г20 вгДомашнее задание 2, № 5 и 6
- 57. Составление формул по заданным таблицам истинностиПолучение совершенно
- 58. Получение совершенно нормальной дизъюнктивной формы (СНДФ)Составление формул
- 59. Получение совершенной конъюнктивной формы (СНКФ)Составление формул по
- 60. Схема одноразрядного сумматора
- 61. ЗадачаСудейская коллегия, состоящая из 3 человек, выносит
- 62. 5.13. Как решать логические задачи? Разнообразие логических
- 63. I. Решение логических задач средствами алгебры логикиОбычно
- 64. Пример 1.Трое друзей, болельщиков автогонок "Формула-1", спорили
- 65. Решение.Введем обозначения для логических высказываний: Ш —
- 66. Учитывая то, что предположения двух друзей подтвердились,
- 67. Пример 2.Некий любитель приключений отправился в кругосветное
- 68. Инструкция по выявлению неисправных узлов такова: если
- 69. РешениеРешение. Введем обозначения для логических высказываний: a — неисправен узел а;
- 70. Выражая импликацию через дизъюнкцию и отрицание (напомним,
- 71. Какие изъяны он обнаружил в инструкции?
- 72. II. Решение логических задач табличным способом При
- 73. Пример 3. В симфонический оркестр приняли на
- 74. Из условия 4 следует, что Смит не
- 75. Пример 4. Три одноклассника — Влад, Тимур
- 76. Определите, кто чем любит заниматься в свободное
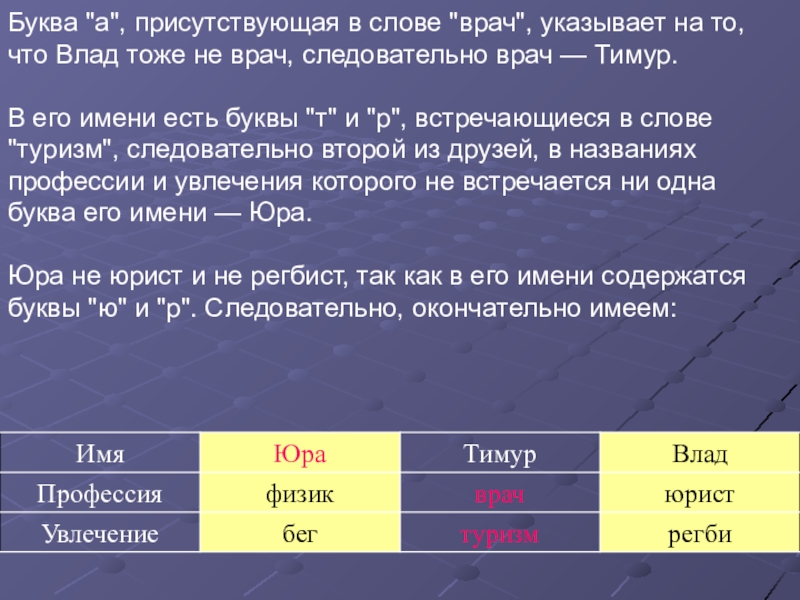
- 77. Буква "а", присутствующая в слове "врач", указывает
- 78. Пример 5. Три дочери писательницы Дорис Кей
- 79. Решение. Составим таблицу и отразим в ней
- 80. Согласно условию 2, парижанка не снимается в
- 81. III. Решение логических задач с помощью рассуждений Этим способом обычно решают несложные логические задачи.
- 82. Пример 6. Вадим, Сергей и Михаил изучают
- 83. Решение. Имеется три утверждения: Вадим изучает китайский;Сергей
- 84. Пример 7. В поездке пятеро друзей —
- 85. Решение. Обозначим высказывательную форму "юноша по имени
Слайд 1Логические основы ПК
Основные понятия математической логики
Простейшие логические операции
Основные законы алгебры логики
Слайд 2Введение в алгебру логики
«Я, по крайней мере, думал,
что противоречить друг
Д. Гильберт
Слайд 3Логика – наука о законах мышления и его формах. Происходит от
Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.
Существуют алгебры натуральных чисел, многочленов, векторов, матриц, множеств и т. д.
Слайд 4Алгебра логики
изучает свойства функций, у которых и аргументы, и значения
Иногда вместо термина «алгебра логики» употребляют термин «двузначная логика», «бинарная логика».
Слайд 5
Родоначальник –
Аристотель (IV век до н. э) –
появление формальной
Последователь –
Лейбниц (XVII век) –
появление математической (символической) логики.
Лейбниц Готфрид Вильгельм
Аристотель
Родоначальник –
Аристотель (IV век до н. э) –
появление формальной логики – рассуждения.
Последователь –
Лейбниц (XVII век) –
появление математической (символической) логики.
Слайд 6Дж. Буль (1815-1864)
Отцом алгебры логики по праву считается английский математик XIX
К. Шеннон (1916-2001)
Долгое время алгебра логики была известна достаточно узкому классу специалистов. Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 году выдающийся американский математик и инженер Клод Шеннон (1916-2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования релейно-контактных и электронно-ламповых схем.
Шеннон Клод Элвуд
Джордж Буль
Слайд 7Большой вклад в становление и развитие алгебры логики внесли
Августус де Морган
Уильям Стенли Джевонс (1835-1882),
Платон Сергеевич Порецкий (1846-1907),
Чарлз Сандерс Пирс (1839-1914),
Андрей Андреевич Марков (1903-1979),
Андрей Николаевич Колмогоров (1903-1987)
и др.
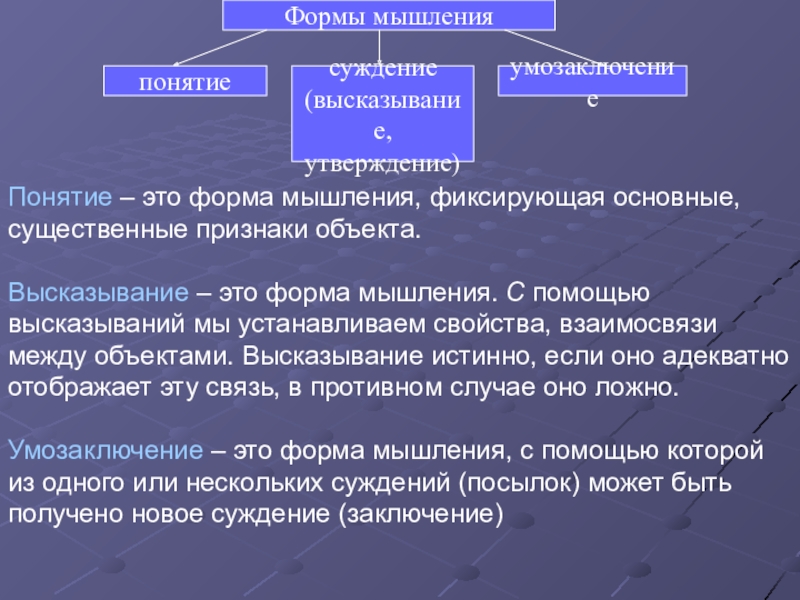
Слайд 9Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
Высказывание –
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение)
Слайд 10Высказывание
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается
Высказывание может быть либо истинно, либо ложно;
Высказывания могут быть выражены с помощью естественных и формальных языков;
Высказывания могут быть выражены только повествовательным предложением;
Высказывания могут быть простыми и составными;
Истинность простых высказываний определяется на основании здравого смысла;
Истинность составных высказываний определяется с помощью алгебры высказываний.
Слайд 11Об истинности высказываний
Это не простой вопрос.
Например, высказывание
«Число 1 +2
В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
Что же является высказыванием в формальной логике?
Слайд 12
Высказывание — это языковое образование, в отношении которого имеет смысл говорить
(Аристотель).
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно
Слайд 13Не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения
Слайд 14Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если...
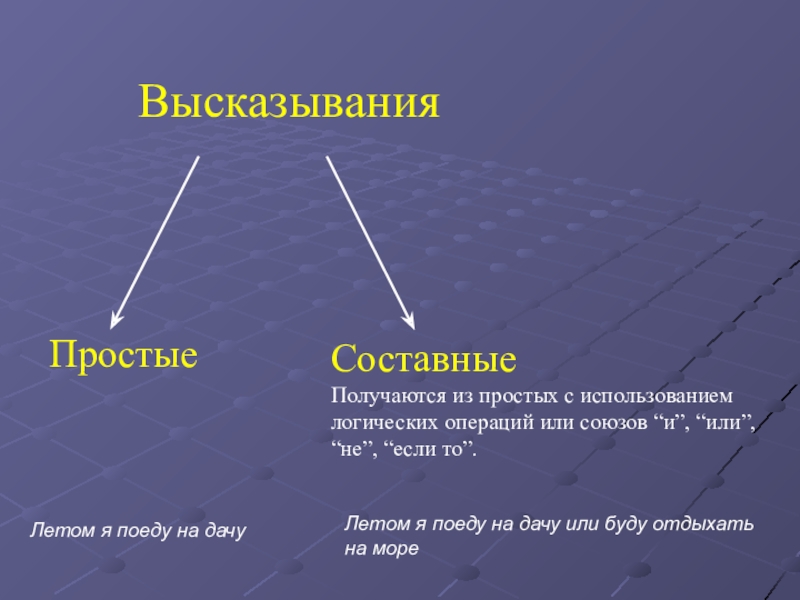
Слайд 15Высказывания
Простые
Составные
Получаются из простых с использованием логических операций или союзов “и”, “или”,
Летом я поеду на дачу
Летом я поеду на дачу или буду отдыхать на море
Слайд 16"Петров — врач", "Петров — шахматист"
"и"
"Петров — врач и
понимаемое как "Петров — врач, хорошо играющий в шахматы".
"или"
"Петров — врач или шахматист",
понимаемое в алгебре логики как
"Петров или врач, или шахматист, или и врач и шахматист одновременно".
Слайд 17Вопросы
Страница 135
№1
Установите, какие из следующих высказываний являются логическими высказываниями, а какие
Какие из высказываний истинны, а какие - нет
Солнце есть спутник Земли
2 + 3 = 4
Сегодня отличная погода
В романе Л.Н. Толстого «Война и мир» 3 432 536 слов
Санкт-Петербург расположен на Неве
Музыка Баха слишком сложна
Первая космическая скорость равна 7.8 км/сек
Как пройти в библиотеку?
Если один угол в треугольнике прямой, то треугольник тупоугольный
Картины Пикассо слишком абстрактны.
Число 2 является делителем числа 7 в некоторой системе счисления.
Слайд 18Вывод:
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно
Слайд 20Алгебра логики изучает строение (форму, структуру) сложных логических высказываний и способы
Слайд 21Простейшие логические операции
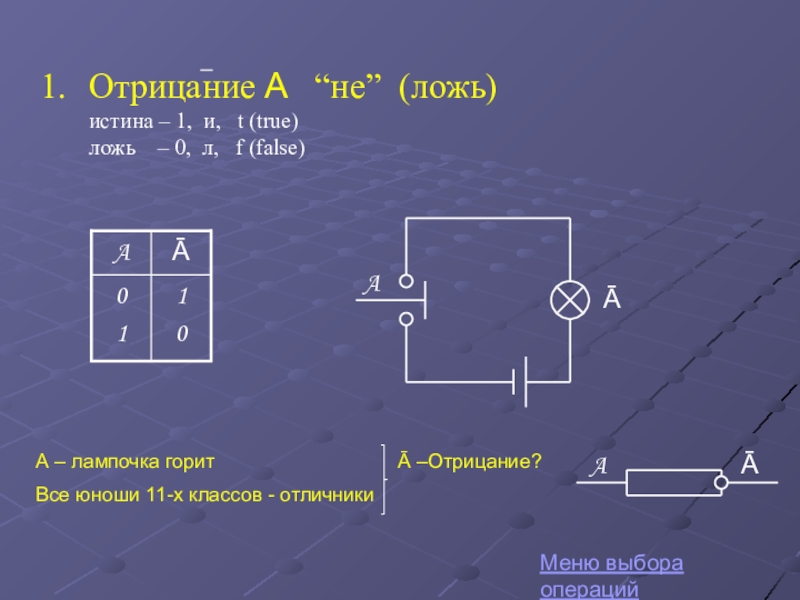
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность
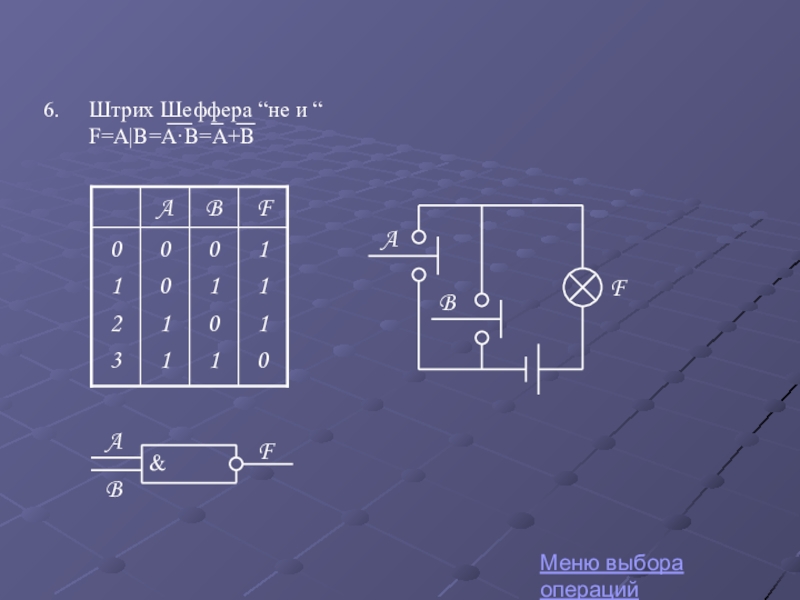
Штрих Шеффера
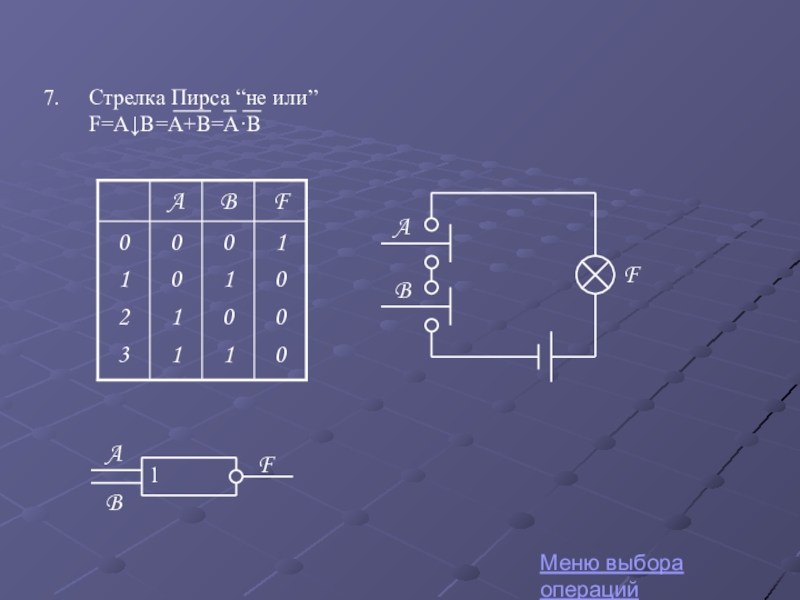
Стрелка Пирса
Переход к разделу «Законы логики»
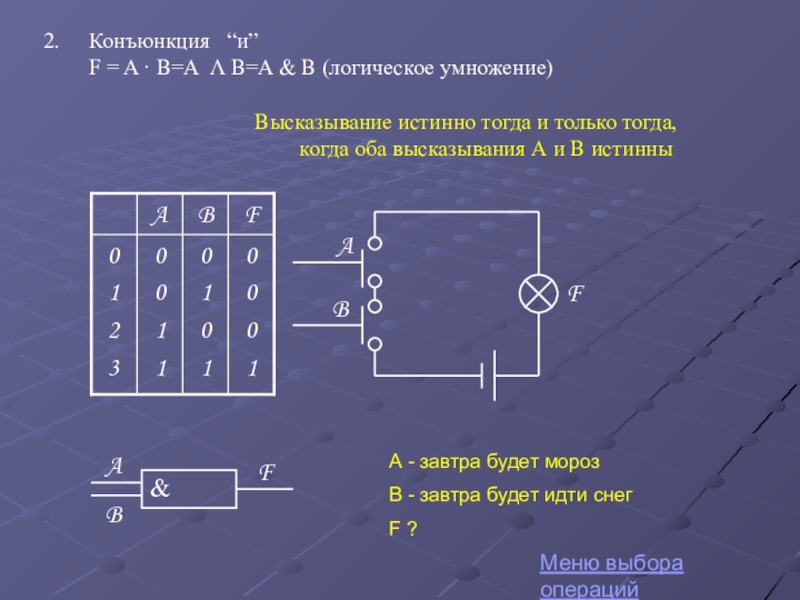
Слайд 23Конъюнкция “и”
F = A · B=A Λ B=A & B
F
A
B
Меню выбора операций
Высказывание истинно тогда и только тогда,
когда оба высказывания А и В истинны
А - завтра будет мороз
В - завтра будет идти снег
F ?
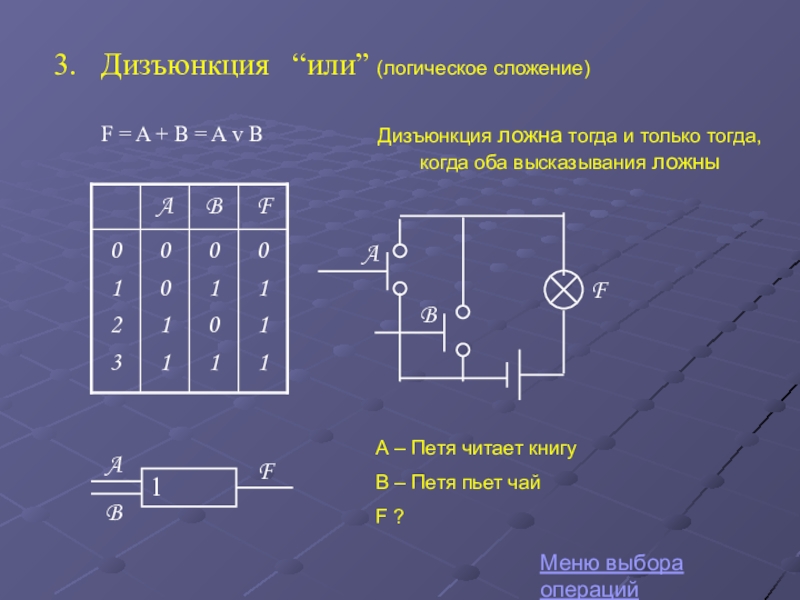
Слайд 24Дизъюнкция “или” (логическое сложение)
F = A + B = A
F
A
B
Меню выбора операций
А – Петя читает книгу
В – Петя пьет чай
F ?
Дизъюнкция ложна тогда и только тогда, когда оба высказывания ложны
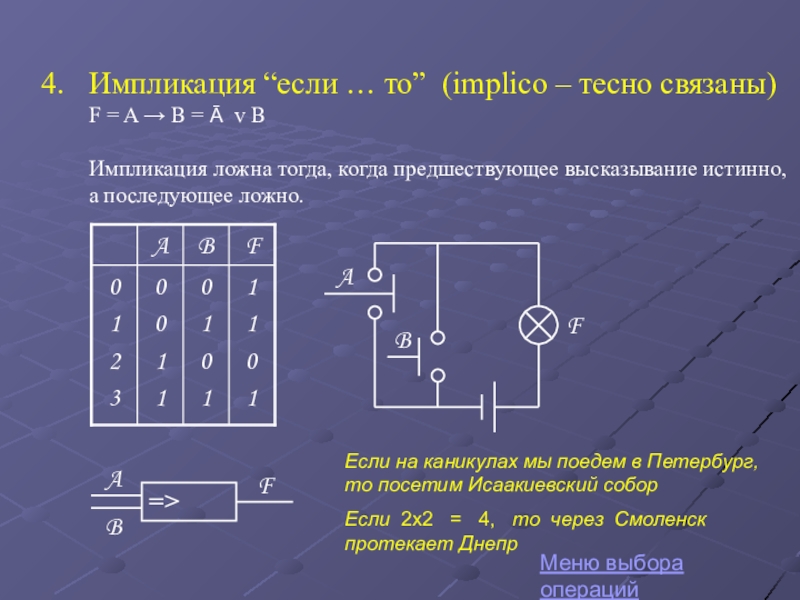
Слайд 25Импликация “если … то” (implico – тесно связаны)
F = A →
Импликация ложна тогда, когда предшествующее высказывание истинно, а последующее ложно.
Меню выбора операций
Если на каникулах мы поедем в Петербург, то посетим Исаакиевский собор
Если 2x2 = 4, то через Смоленск протекает Днепр
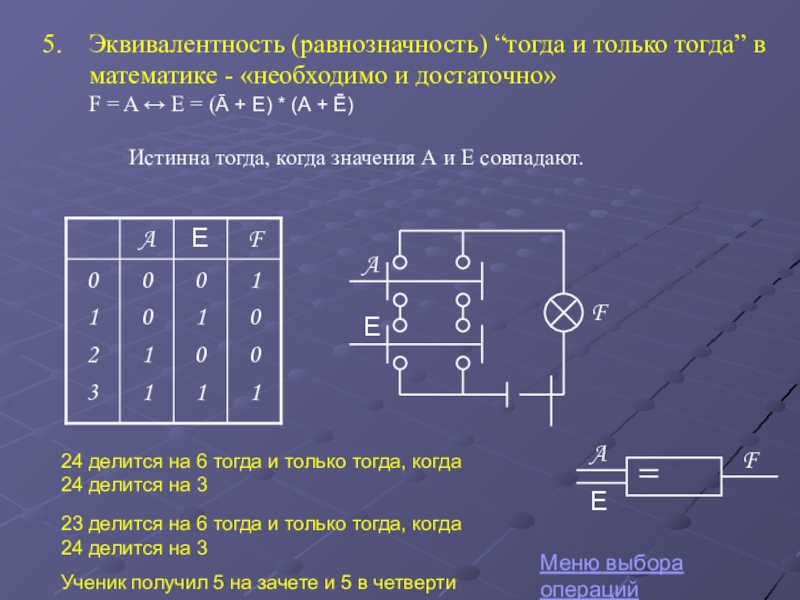
Слайд 26Эквивалентность (равнозначность) “тогда и только тогда” в математике - «необходимо и
F = A ↔ Е = (Ā + Е) * (А + Ē)
Истинна тогда, когда значения А и Е совпадают.
Меню выбора операций
24 делится на 6 тогда и только тогда, когда 24 делится на 3
23 делится на 6 тогда и только тогда, когда 24 делится на 3
Ученик получил 5 на зачете и 5 в четверти
Слайд 30Законы логики
x ≡ x закон тождества
x · x = 0 закон противоречия
x +
x = x закон двойного отрицания
x · x = x закон идемпотентности
x + x = x
x · y = y · x закон переместительный или
x + y = y + x коммутативный
x · y · z = x · ( y · z ) закон сочетательный или
x + y + z = x + ( y + z ) ассоциативный
x · ( y +z ) = x · y + x · z закон распределительный или
x + ( y · z) = ( x + y ) ( x + z ) дистрибутивный
x · y = x + y закон Моргана
x + y = x · y
=
Слайд 33Задание на дом
П. 5.9 Основные законы алгебры логики
П.5.10 Составление таблиц истинности
Доказать правила де Моргана при помощи таблиц истинности
Упр 10 (ж-м)
Упр 13 (а,б,г)
Слайд 34
Самостоятельная работа
ВАРИАНТ 1
Определите, является ли указанная формула тождественно истинной или тождественно
Пусть a = "это утро ясное", а b = "это утро теплое". Выразите следующие формулы на обычном языке:
ВАРИАНТ 2
Определите, является ли указанная формула тождественно истинной или тождественно ложной:
Пусть a = "это утро ясное", а b = "это утро теплое". Выразите следующие формулы на обычном языке:
Слайд 355.11. Как упростить логическую формулу?
Под упрощением формулы, не содержащей операций импликации
Слайд 36
x+y * (x*y) = x*y*x*y = x*x*y*y = 0 * y
x*y v x v y v x = x*y + x + y + x = x*y + x*y + x =
x*(y + y) + x = x + x = 1
(x v y)(x v y)(x v y) = (x + y)(x + y)(x + y)(x + y) =
y * x
Как упростить логическую формулу
x+y * (x*y) = x*y*x*y = x*x*y*y = 0 * y = 0
x*y v x v y v x = x*y + x + y + x = x*y + x*y + x =
x*(y + y) + x = x + x = 1
(x v y)(x v y)(x v y) = (x + y)(x + y)(x + y)(x + y) =
y * x
Слайд 37
Как упростить логическую формулу
x*y v x*y*z v x*z = x*y+x*y*z +
x*y+x*y*z + x*z*y+x*z*y =
(x*y+x*y*z) + (x*z*y+x*z*y) = x*y(1+z) + y*z(x+x)
= x*y + y*z
x*y+z = x*y*z = (x+y)*z
Слайд 40Самостоятельная работа
Вариант 1
а)
б)
Вариант 2
а)
б)
Упростите следующие формулы, используя законы поглощения:
«Я поеду в Москву и, если встречу там друзей, то мы интересно проведём время»
A /\ (B → C)
(A /\ B) →C \/ D
(A /\ B) ↔ (C /\ D)
A /\ B → C
«Если вы были в Париже, то вы видели Лувр или видели Эйфелеву башню»
A → (C /\ D)
(A /\ B) →C \/ D
(A /\ B) ↔ (C /\ D)
A → (C \/ D)
А9. Какова формула логического высказывания
Слайд 41Что такое переключательная схема?
Переключательная схема – это схематичное изображение некоторого устройства,
Каждый переключатель имеет только два состяния: замнутое и разомкнутое
Когда состояние замкнутое X=1, когда разомкнутое - X=0
Всей переключательной схеме можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю — если не проводит.
Эта переменная называется функцией проводимости.
Слайд 42Функции проводимости F некоторых переключательных схем:
a)
б) Схема содержит один постоянно разомкнутый контакт, следовательно F=0;
в) Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x;
г) Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) = ;
Слайд 43Функции проводимости F некоторых переключательных схем:
д) Схема проводит ток, когда оба
е) Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно, F(x)=x+y;
ж) Схема состоит из двух параллельных ветвей и описывается функцией
Слайд 44Синтез и анализ схемы
СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится
составлению функции проводимости по таблице истинности, отражающей эти условия;
упрощению этой функции;
построению соответствующей схемы.
АНАЛИЗ СХЕМЫ сводится к
определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных.
получению упрощённой формулы.
Слайд 45Примеры
1. Построить схему, содержащую 4 переключателя x, y, z и t,
Решение. В этом случае можно обойтись без построения таблицы истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) = t * (x + y + z), а схема выглядит так:
Слайд 46Примеры
2. Построим схему с пятью переключателями, которая проводит ток в том
Схема имеет вид:
Слайд 47Примеры
3. Найдем функцию проводимости схемы:
Решение. Имеется четыре возможных пути прохождения
Функция проводимости
F(a, b, c, d, e) = a * b + a * e * d + c * d + c * e * b
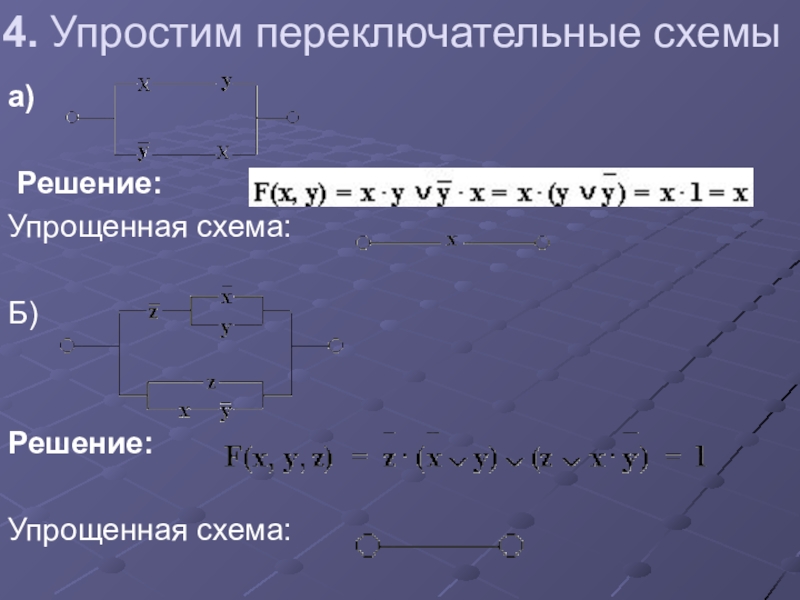
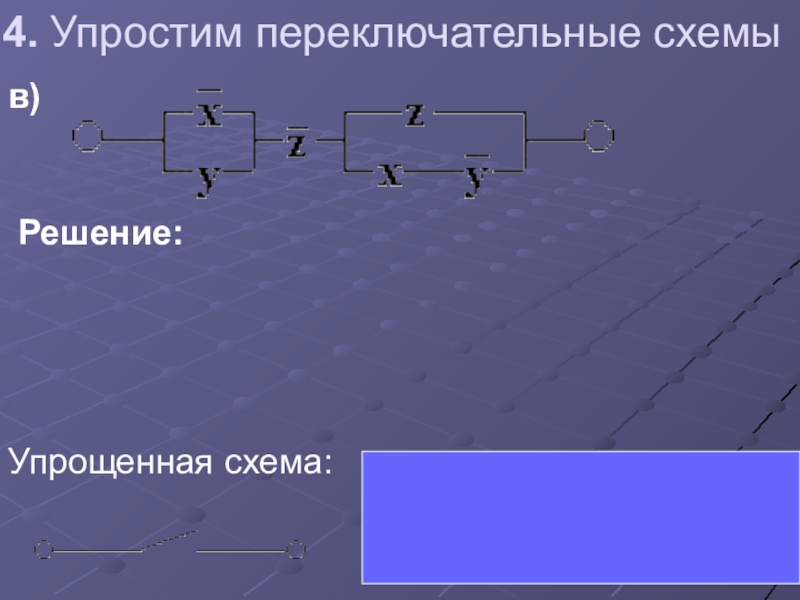
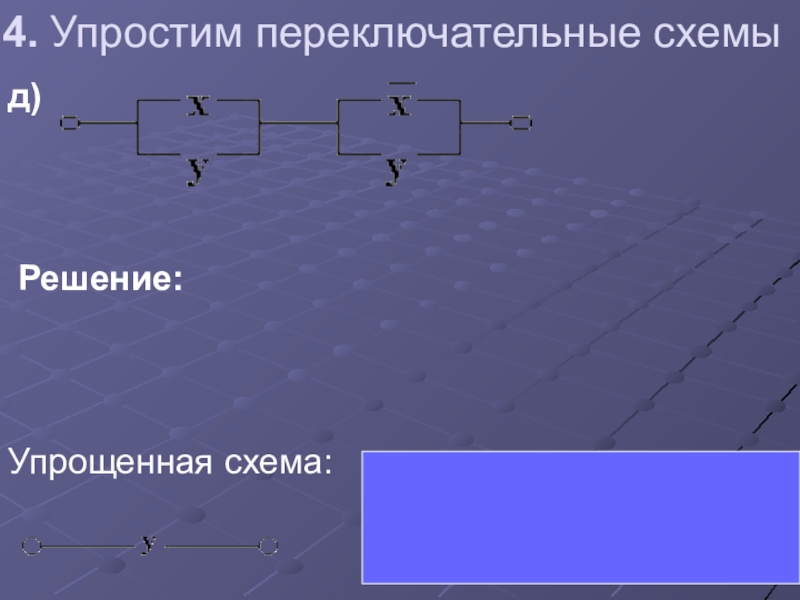
Слайд 484. Упростим переключательные схемы
а)
Решение:
Упрощенная схема:
Б)
Решение:
Упрощенная схема:
Слайд 57Составление формул по заданным таблицам истинности
Получение совершенно нормальной дизъюнктивной формы (СНДФ)
Получение
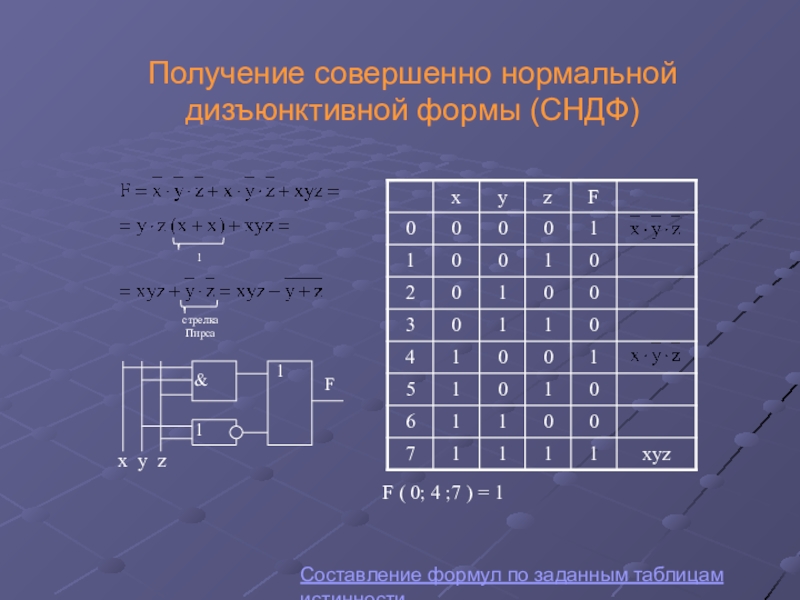
Слайд 58Получение совершенно нормальной дизъюнктивной формы (СНДФ)
Составление формул по заданным таблицам истинности
1
стрелка
Пирса
F
Слайд 59Получение совершенной конъюнктивной формы (СНКФ)
Составление формул по заданным таблицам истинности
F (
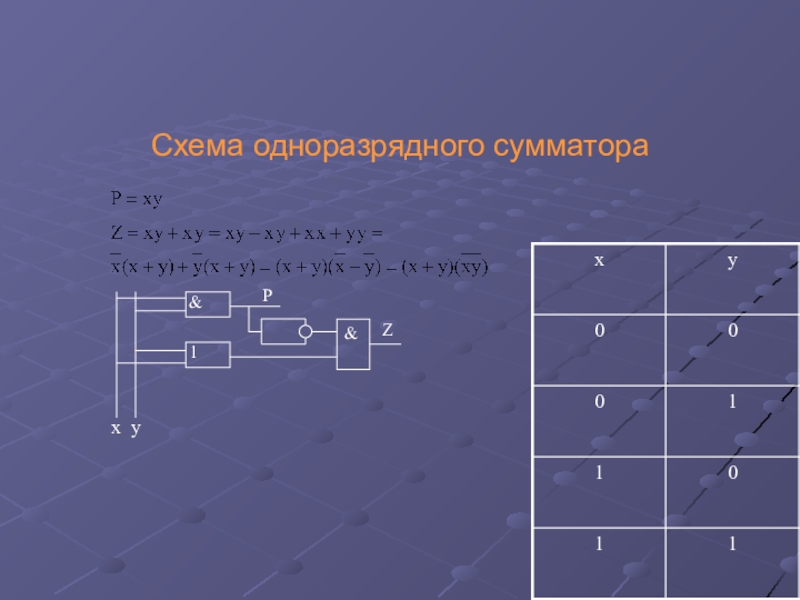
Слайд 61Задача
Судейская коллегия, состоящая из 3 человек, выносит решение большинством голосов. Построить
011 101 110 111
1
Слайд 625.13. Как решать логические задачи?
Разнообразие логических задач очень велико. Способов их
средствами алгебры логики;
табличный;
с помощью рассуждений.
Познакомимся с ними поочередно.
Слайд 63I. Решение логических задач средствами алгебры логики
Обычно используется следующая схема решения:
изучается условие задачи;
вводится система обозначений для логических высказываний;
конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
определяются значения истинности этой логической формулы;
из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Слайд 64Пример 1.
Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Слайд 65Решение.
Введем обозначения для логических высказываний:
Ш — победит Шумахер; Х —
Реплика Ника "Алези пилотирует самую мощную машину" не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Слайд 66Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны,
Высказывание
истинно только при Ш=1, А=0, Х=0.
Ответ. Победителем этапа гонок стал Шумахер.
Слайд 67Пример 2.
Некий любитель приключений отправился в кругосветное путешествие на яхте, оснащённой
Слайд 68Инструкция по выявлению неисправных узлов такова:
если неисправен хотя бы один
если неисправен узел a, но исправен узел с, то загорается лампочка y;
если неисправен узел с, но исправен узел b, загорается лампочка y, но не загорается лампочка x;
если неисправен узел b, но исправен узел c, то загораются лампочки x и y или не загорается лампочка x;
если горит лампочка х и при этом либо неисправен узел а, либо все три узла a, b, c исправны, то горит и лампочка y.
В пути компьютер сломался. На контрольной панели загорелась лампочка x. Тщательно изучив инструкцию, путешественник починил компьютер. Но с этого момента и до конца плавания его не оставляла тревога. Он понял, что инструкция несовершенна, и есть случаи, когда она ему не поможет.
Какие узлы заменил путешественник? Какие изъяны он обнаружил в инструкции?
Слайд 69Решение
Решение. Введем обозначения для логических высказываний:
a — неисправен узел а; x — горит лампочка х;
b — неисправен узел b;
с — неисправен узел с; z — горит лампочка z.
Правила 1-5 выражаются следующими формулами:
Формулы 1-5 истинны по условию, следовательно, их конъюнкция тоже истинна:
Слайд 70Выражая импликацию через дизъюнкцию и отрицание (напомним, что
), получаем:
Подставляя
Отсюда следует, что a=0, b=1, c=1.
Ответ на первый вопрос задачи: нужно заменить блоки b и c; блок а не требует замены.
Слайд 72II. Решение логических задач табличным способом
При использовании этого способа условия, которые
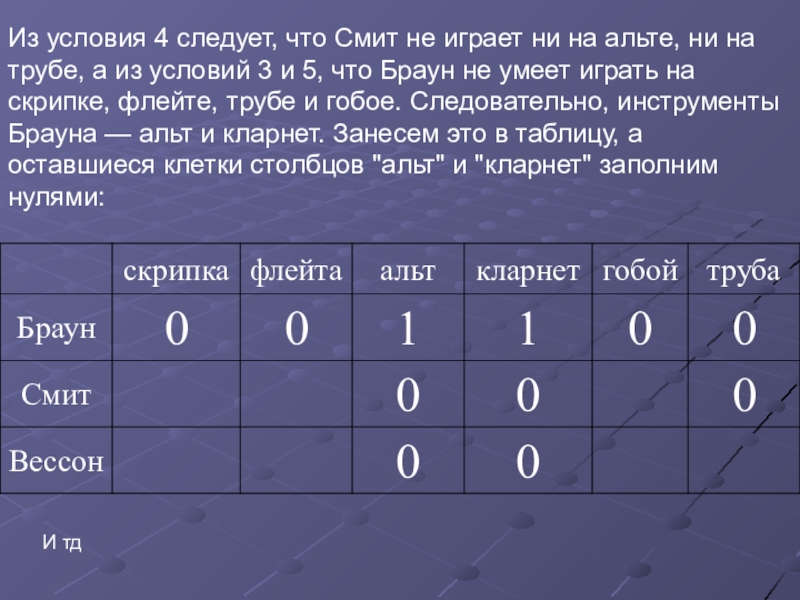
Слайд 73Пример 3. В симфонический оркестр приняли на работу трёх музыкантов: Брауна,
Известно, что:
Смит самый высокий;
играющий на скрипке меньше ростом играющего на флейте;
играющие на скрипке и флейте и Браун любят пиццу;
когда между альтистом и трубачом возникает ссора, Смит мирит их;
Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Слайд 74Из условия 4 следует, что Смит не играет ни на альте,
И тд
Слайд 75Пример 4. Три одноклассника — Влад, Тимур и Юра, встретились спустя
Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист.
Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Слайд 76Определите, кто чем любит заниматься в свободное время и у кого
Решение. Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение).
Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.
Слайд 77Буква "а", присутствующая в слове "врач", указывает на то, что Влад
В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра.
Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем:
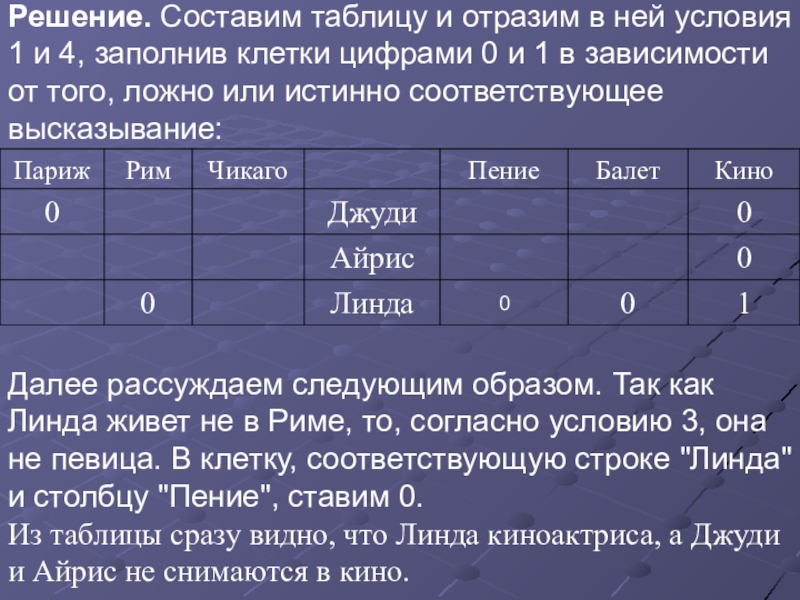
Слайд 78Пример 5. Три дочери писательницы Дорис Кей — Джуди, Айрис и
Они приобрели известность в разных видах искусств — пении, балете и кино.
Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго.
Известно, что:
Джуди живет не в Париже, а Линда — не в Риме;
парижанка не снимается в кино;
та, кто живет в Риме, певица;
Линда равнодушна к балету.
Где живет Айрис, и какова ее профессия?
Слайд 79Решение. Составим таблицу и отразим в ней условия 1 и 4,
Далее рассуждаем следующим образом. Так как Линда живет не в Риме, то, согласно условию 3, она не певица. В клетку, соответствующую строке "Линда" и столбцу "Пение", ставим 0.
Из таблицы сразу видно, что Линда киноактриса, а Джуди и Айрис не снимаются в кино.
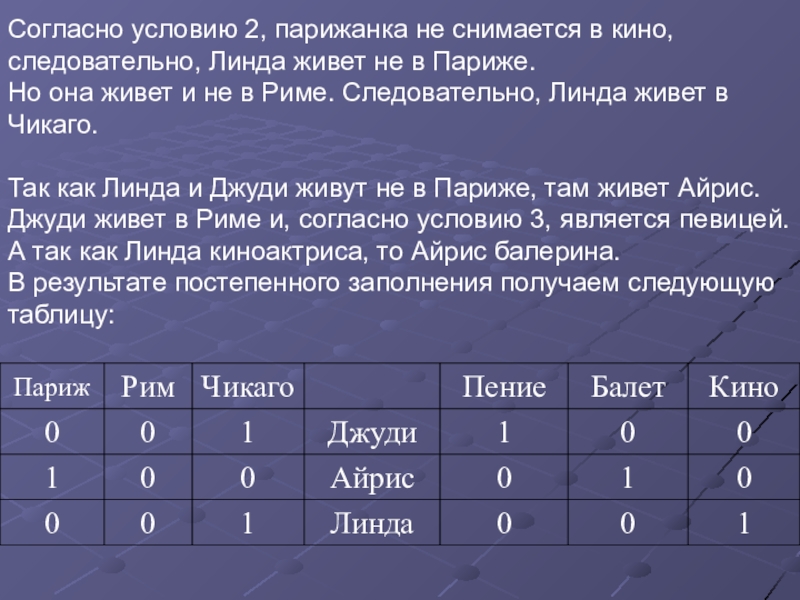
Слайд 80Согласно условию 2, парижанка не снимается в кино, следовательно, Линда живет
Но она живет и не в Риме. Следовательно, Линда живет в Чикаго.
Так как Линда и Джуди живут не в Париже, там живет Айрис. Джуди живет в Риме и, согласно условию 3, является певицей. А так как Линда киноактриса, то Айрис балерина.
В результате постепенного заполнения получаем следующую таблицу:
Ответ. Айрис балерина. Она живет в Париже.
Слайд 81III. Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные
Слайд 82Пример 6. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский,
На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский".
Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны.
Какой язык изучает каждый из молодых людей?
Слайд 83Решение. Имеется три утверждения:
Вадим изучает китайский;
Сергей не изучает китайский;
Михаил не
Если верно второе утверждение, то первое и третье должны быть ложны.
При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
Слайд 84Пример 7. В поездке пятеро друзей — Антон, Борис, Вадим, Дима
Они предложили ей отгадать их фамилии, причём каждый из них высказал одно истинное и одно ложное утверждение:
Дима сказал: "Моя фамилия — Мишин, а фамилия Бориса — Хохлов".
Антон сказал: "Мишин — это моя фамилия, а фамилия Вадима — Белкин".
Борис сказал: "Фамилия Вадима — Тихонов, а моя фамилия — Мишин".
Вадим сказал: "Моя фамилия — Белкин, а фамилия Гриши — Чехов".
Гриша сказал: "Да, моя фамилия Чехов, а фамилия Антона — Тихонов".
Какую фамилию носит каждый из друзей?
Слайд 85Решение. Обозначим высказывательную форму "юноша по имени А носит фамилию Б"
Зафиксируем высказывания каждого из друзей:
ДМ и БХ;
АМ и ВБ;
ВТ и БМ;
ВБ и ГЧ;
ГЧ и АТ.
Допустим сначала, что истинно ДМ. Но, если истинно ДМ, то у Антона и у Бориса должны быть другие фамилии, значит АМ и БМ ложно. Но если АМ и БМ ложны, то должны быть истинны ВБ и ВТ, но ВБ и ВТ одновременно истинными быть не могут.
Значит остается другой случай: истинно БХ. Этот случай приводит к цепочке умозаключений: БХ истинно
БМ ложно
ВТ истинно
АТ ложно
ГЧ истинно
ВБ ложно
АМ истинно.
Ответ: Борис — Хохлов, Вадим — Тихонов, Гриша — Чехов, Антон — Мишин, Дима — Белкин.