- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Измерение количества информации (СПО, 1 курс)
Содержание
- 1. Измерение количества информации (СПО, 1 курс)
- 2. Существуют различные подходы к измерению количества информации:1)
- 3. 1. АЛФАВИТНЫЙ ПОДХОД Алфавитный подход основан
- 4. Основоположником алфавитного подхода измерения информации является великий российский ученый-математик Андрей Николаевич Колмогоров (1903-1987).
- 5. Обычно под алфавитом понимают только буквы, но
- 6. При алфавитном подходе считается, что каждый символ
- 7. При алфавитном подходе к измерению информации количество
- 8. 3) алфавит десятичной системы счисления – это
- 9. МОЩНОСТЬ АЛФАВИТА число символов в алфавите (его
- 10. ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИСИМВОЛЬНЫЙ АЛФАВИТ КОМПЬЮТЕРА русские (РУССКИЕ)
- 11. Скорость передачи информацииПрием-передача информации могут происходить с
- 12. Пример 1. Подсчитайте объем информации, содержащейся в
- 13. Пример 2. На диске объемом 100 Мбайт
- 14. Домашнее задание. ЗАДАЧА 1
- 15. 2. СОДЕРЖАТЕЛЬНЫЙ ПОДХОД(количество информации зависит от ее
- 16. Информация — это знания людей, получаемые ими
- 17. Вероятность некоторого события — это величина, которая
- 18. Формула, используемая для вычисления количества информации, зависит
- 19. Равновероятные события. 2i = N 1 бит
- 20. Примеры.Пример 1. Сколько информации содержит сообщение о
- 21. Пример 2. Сколько информации содержит сообщение о
- 22. Данную задачу можно решить иначе:Из уравнения Хартли
- 23. 2i = 1/p Решая данное показательное уравнение
- 24. Пример 3. На автобусной остановке останавливаются два
- 25. Решение. Студент провел исследование. В течение всего
- 26. Пример 4. Рассмотрим другой вариант задачи об
- 27. Вывод: уменьшение вероятности события в 2 раза
- 28. Решение задач
Слайд 1Лекция. Различные подходы к измерению количества информации.
Преподаватель математики и информатики
Подосинникова Е.А.
ГОАПОУ
Слайд 2Существуют различные подходы к измерению количества информации:
1) Алфавитный
2) Содержательный
3) Вероятностный
Количество
Слайд 31. АЛФАВИТНЫЙ ПОДХОД
Алфавитный подход основан на подсчете числа символов
Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.
Данный подход удобен при использовании технических средств работы с информацией, т.к. не учитывается содержание сообщения.
Слайд 4Основоположником алфавитного подхода измерения информации является великий российский ученый-математик Андрей Николаевич
Слайд 5Обычно под алфавитом понимают только буквы, но поскольку в тексте могут
Ограничений на максимальную (max) мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере.
Поскольку 256=28, то 1символ несет в тексте 8 бит информации.
АЛФАВИТ – это вся совокупность символов, используемых в некотором языке для представления информации.
Алфавитный подход – как способ измерения информации.
Слайд 6
При алфавитном подходе считается, что каждый символ текста имеет определенный «информационный
Алфавит, который содержит наименьшее число символов, используется в компьютере. Он содержит всего два символа 0 и 1 и называется двоичным алфавитом.
Информационный вес символа двоичного алфавита принят за единицу информации и называется 1 бит.
Например, чтобы посчитать количество информации в следующем двоичном тексте 110011111100101000101011, нужно пересчитать все 0 и 1.
В тексте содержится 24 бита информации.
Слайд 7При алфавитном подходе к измерению информации количество информации зависит не от
МОЩНОСТЬ АЛФАВИТА (N) – это полное число символов в алфавите.
Например,
1) мощность русского алфавита составляет N=33;
2) мощность английского алфавита N= ?
Слайд 83) алфавит десятичной системы счисления – это множество цифр- 0,1,2,3,4,5,6,7,8,9.
Мощность такого
4) Компьютерный алфавит, используемый для представления текстов в компьютере, использует 256 символов, т.е. N=256
5) Алфавит двоичной системы кодирования информации имеет всего два символа-
0 и 1, поэтому N=2.
Замечание. С увеличением мощности алфавита увеличивается информационный вес символов этого алфавита.
Слайд 9
МОЩНОСТЬ АЛФАВИТА
число символов в алфавите (его размер)
N
ИНФОРМАЦИОННЫЙ ВЕС СИМВОЛА
количество информации
I = K ∙ i
i
2 i = N
Информационный вес каждого символа (i) и
мощность алфавита (N) связаны формулой:
Количество (объем) информации в сообщении (I) можно посчитать по формуле:
Количество информации в сообщении или информационный объём текста (I), равен количеству информации, которое несет один символ (i), умноженное на количество символов K в сообщении, т.е. I = K ∙ i
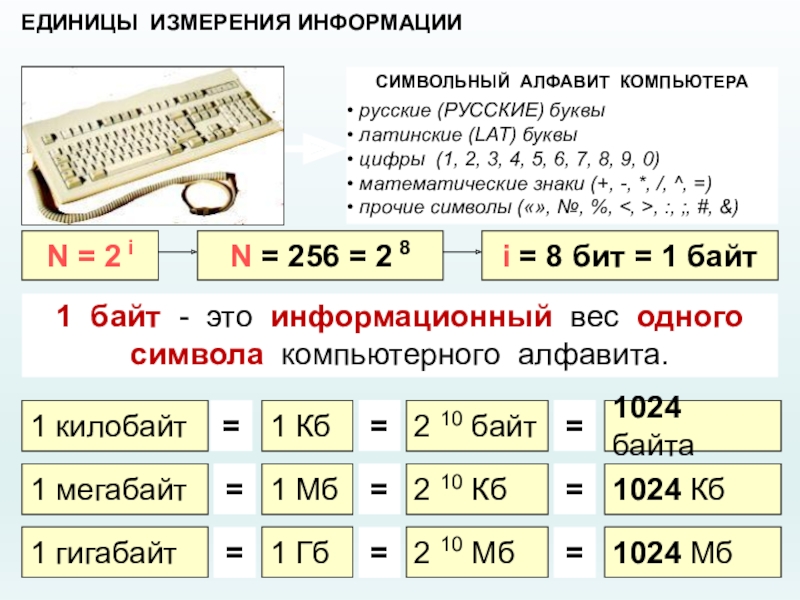
Слайд 10ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ
СИМВОЛЬНЫЙ АЛФАВИТ КОМПЬЮТЕРА
русские (РУССКИЕ) буквы
латинские (LAT) буквы
математические знаки (+, -, *, /, ^, =)
прочие символы («», №, %, <, >, :, ;, #, &)
1 байт - это информационный вес одного символа компьютерного алфавита.
Слайд 11Скорость передачи информации
Прием-передача информации могут происходить с разной скоростью.
Количество информации, передаваемое
Единицы измерения скорости передачи информации: бит в секунду (бит/с), байт в секунду (байт/с), килобайт в секунду (Кбайт/с) и т.д.
Слайд 12Пример 1. Подсчитайте объем информации, содержащейся в романе А. Дюма "Три
Решение.
590*48*53=1500960(символов).
Информационный вес одного символа, по определению, составляет 1 байт, тогда:
1500960байт=1466Кбайт= 1,4Мбайт.
3) На одном лазерном диске емкостью 600 Мбайт можно разместить 600 : 1,4 = 428, 57, т.е около 428 произведений, близких по объему к роману А. Дюма "Три мушкетера".
Ответ: I = 1,4 Мб; 428 книг.
Слайд 13Пример 2. На диске объемом 100 Мбайт подготовлена к выдаче на
Решение.
К = 24*80=1920 (символов)
Т.к. информационный вес одного символа компьютерного алфавита составляет 1 байт, то I = 1920 байт.
Объем диска 100*1024*1024 байт = 104857600 байт
1920/104857600=0,000018 (часть диска).
Ответ: 0,000018 часть диска.
Слайд 14Домашнее задание.
ЗАДАЧА 1
Книга,
ЗАДАЧА 2
Текст составлен с помощью алфавита мощностью в 64 символа и содержит 100 символов. Каков информационный объем текста.
ЗАДАЧА 3
Сообщение записано буквами из 16 символьного алфавита, содержит 50 символов. Какой объем информации оно несет.
ЗАДАЧА 4
Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 32 символа, второй – мощностью 64 символа. Во сколько раз отличатся количество информации в этих текстах.
Слайд 152. СОДЕРЖАТЕЛЬНЫЙ ПОДХОД
(количество информации зависит от ее содержания)
Основоположником этого подхода является
По Шеннону, информация — это мера уменьшения неопределенности наших знаний.
Неопределенность некоторого события — это количество возможных исходов данного события.
Слайд 16Информация — это знания людей, получаемые ими из различных сообщений.
Сообщение
Сообщение
Информативное, если оно пополняет знания человека, т.е. несет для него информацию.
Количество информации в информативном сообщении больше нуля.
Неинформативное, если это:
«старые» сведения, т.е. человек это уже знает;
содержание сообщения непонятно человеку.
Количество информации в неинформативном сообщении равно нулю.
Слайд 17Вероятность некоторого события — это величина, которая может принимать значения от
Вероятность некоторого события определяется путем многократных наблюдений (измерений, испытаний). Такие измерения называют статистическими. И чем большее количество измерений выполнено, тем точнее определяется вероятность события.
ОПРЕДЕЛЕНИЯ
Слайд 18Формула, используемая для вычисления количества информации, зависит от ситуаций, которых может
1. Все возможные варианты события равновероятны. Их число равно N.
2. Вероятности (p) возможных вариантов события разные и они заранее известны:
{pi }, i = 1..N.
Здесь по-прежнему N-число возможных вариантов события.
Слайд 19Равновероятные события.
2i = N
1 бит — это количество информации
Формула Хартли — это показательное уравнение. Если i неизвестная величина, то решением данного уравнения будет:
i = log2N
Данные формулы тождественны друг другу.
События равновероятны, если ни одно из них не имеет преимущества перед другими.
Если обозначить буквой i количество информации в сообщении о том, что произошло одно из N равновероятных событий, то величины i и N связаны между собой формулой Хартли:
Слайд 20Примеры.
Пример 1. Сколько информации содержит сообщение о том, что из колоды
Решение: В колоде 32 карты. В перемешанной колоде выпадение любой карты — равновероятные события. Если i — количество информации в сообщении о том, что выпала конкретная карта (например, дама пик), то из уравнения Хартли:
2i = 32 = 25
Ответ: i = 5 бит.
Слайд 21Пример 2. Сколько информации содержит сообщение о выпадении грани с числом
Решение. Считая выпадение любой грани событием равновероятным, запишем формулу Хартли:
2i = 6.
Ответ: i = log26 = 2,58496 бит.
Слайд 22Данную задачу можно решить иначе:
Из уравнения Хартли имеем: 2i = 6.
Так
2 < i < 3.
Затем определяем более точное значение (с точностью до пяти знаков после запятой), что i = 2,58496 бит.
Замечание. При данном подходе к вычислению количества информации ответ будет выражен дробной величиной.
Слайд 232i = 1/p
Решая данное показательное уравнение относительно i, получаем:
i =
3. Вероятностный подход
Осуществим при неравновероятных событиях.
Неравновероятные события – это события, имеющие разную вероятность реализации.
Если вероятность некоторого события равна p, а i (бит) — это количество информации в сообщении о том, что произошло это событие, то данные величины связаны между собой формулой:
Слайд 24Пример 3. На автобусной остановке останавливаются два маршрута автобусов: № 5
Слайд 25Решение. Студент провел исследование. В течение всего рабочего дня он подсчитал,
p7 = 75/100 = 3/4.
Отсюда, количество информации в сообщении об автобусе № 5 равно: i5 = log24 = 2 бита. Количество информации в сообщении об автобусе № 7 равно:
i7 = log2(4/3) = log24 – log23 = 2 – 1,58496 = 0,41504 бита.
Ответ: i5 = 2 бита; i7 = 0,41504 бита.
Слайд 26Пример 4. Рассмотрим другой вариант задачи об автобусах. На остановке останавливаются
Решение. i5 = 4 бита, p5 = 2 · p7
Вспомним связь между вероятностью и количеством информации: 2i = 1/p
Отсюда: p = 2–i
Подставляя в равенство из условия задачи, получим:
Отсюда:
Слайд 27Вывод: уменьшение вероятности события в 2 раза увеличивает информативность сообщения о
Очевидно и обратное правило: увеличение вероятности события в 2 раза уменьшает информативность сообщения о нем на 1 бит. Зная эти правила, предыдущую задачу можно было решить «в уме».