последние десятилетия увеличение быстродействия компьютеров определяется не только (и не столько) уменьшением тактового периода элементной базы, но и принятием новых решений в архитектуре, в том числе – за счет параллелизма.
Создается программное обеспечение, помогающее эффективно осваивать вычислительные системы с параллельной архитектурой
С быстрым развитием многопроцессорных компьютеров задача создания эффективных параллельных программ существенно усложнилась из-за нехватки должной поддержки со стороны языков программирования, компиляторов, ОС и др., существенно отстающего по сравнению с аппаратными средствами. Фактически, забота об эффективной организации параллельных процессов ложится, в основном, на пользователя.
⇒
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Информационная структура программ. Граф алгоритма. Графовые модели программ.
Содержание
- 1. Информационная структура программ. Граф алгоритма. Графовые модели программ.
- 2. Информационная структура программ (2)⇒ Задача адаптации большого
- 3. Информационная структура программ (3)На таких системах могут
- 4. Информационная структура программ (4)Для исследования тонкой информационной
- 5. Информационная структура программ (5)В системе V-Ray (разработка
- 6. Граф алгоритма (1)Любой компьютерный код описывает семейство
- 7. Граф алгоритма (2)Решение любой задачи (и на
- 8. Граф алгоритма (3)Входные данные представлены как начальные
- 9. Граф алгоритма (4)Итак, каждое описание алгоритма порождает
- 10. Граф алгоритма (5)Каноническая параллельная форма графа. Помечаем
- 11. Граф алгоритма (6)Эквивалентные преобразования графа отражают разные
- 12. Граф алгоритма (7)Выводы (зачем это все надо)Зная
- 13. Граф алгоритма (8)Рассмотрим идею построения алгоритмов малой
- 14. Граф алгоритма (9)Схема сдваивания. Данные: а1, а2,
- 15. Граф алгоритма (10)Существенное снижение высоты произошло за
- 16. Графовые модели программ (1)Не совсем то, что
- 17. Графовые модели программ (2)Операционное отношение Информационное отношение:Здесь вершины – операторыОперационное отношение Информационное отношение:
- 18. Графовые модели программ (3)Тот же цикл, но
- 19. Графовые модели программ (4)Параллельная структура программы –
- 20. Графовые модели программ (5): макро-параллелизм (или конечный)
- 21. Графовые модели программ (6): координатный микро-параллелизм
- 22. Графовые модели программ (7): скошенный микро-параллелизм
- 23. Графовые модели программ (8): эквивалентные преобразованияОдин и
- 24. Графовые модели программ (9): эквивалентные преобразования
- 25. Графовые модели программ (10): пример эквивалентного преобразования цикла
Информационная структура программ (2)⇒ Задача адаптации большого числа существующих программ под новые компьютеры является сложной и актуальной проблемой.При адаптации последовательных программ для параллельных компьютеров необходимо определять целое множество свойств, которые указывают на имеющийся потенциальный параллелизм исследуемых
Слайд 1Информационная структура программ (1)
Три «кита» высокопроизводительных вычислений:
Архитектура вычислительных систем
Технологии параллельных вычислений
Алгоритмы
В
Слайд 2Информационная структура программ (2)
⇒ Задача адаптации большого числа существующих программ под
новые компьютеры является сложной и актуальной проблемой.
При адаптации последовательных программ для параллельных компьютеров необходимо определять целое множество свойств, которые указывают на имеющийся потенциальный параллелизм исследуемых программ и возможные способы их преобразования.
Выявление этих свойств обычно возлагается на пользователя, поскольку методы, использующиеся в штатных компиляторах параллельных систем, как правило, не в состоянии обеспечить достижение нужного уровня производительности.
Для помощи пользователям создаются специальные технологии параллельного программирования и разрабатываются автономные системы анализа структуры программ. Данное направление исследований активно развивается и у нас в стране, и за рубежом для анализа последовательных пользовательских пакетов с точки зрения выявления параллелизма и возможностей эффективного преобразова-ния под требования конкретных параллельных систем.
При адаптации последовательных программ для параллельных компьютеров необходимо определять целое множество свойств, которые указывают на имеющийся потенциальный параллелизм исследуемых программ и возможные способы их преобразования.
Выявление этих свойств обычно возлагается на пользователя, поскольку методы, использующиеся в штатных компиляторах параллельных систем, как правило, не в состоянии обеспечить достижение нужного уровня производительности.
Для помощи пользователям создаются специальные технологии параллельного программирования и разрабатываются автономные системы анализа структуры программ. Данное направление исследований активно развивается и у нас в стране, и за рубежом для анализа последовательных пользовательских пакетов с точки зрения выявления параллелизма и возможностей эффективного преобразова-ния под требования конкретных параллельных систем.
Слайд 3Информационная структура программ (3)
На таких системах могут быть реализованы самые передовые
идеи исследования и эквивалентного преобразования программ. К таким инструментам относятся системы КАР, Forge, V-Ray (НИВЦ).
С помощью таких систем можно значительно уменьшить время работы программ на параллельных системах по сравнению со временем, которое показывают те же программы, пропущенные через штатный компилятор. Ускорение в несколько раз удается получить, даже если программы предварительно оптимизируются вручную.
Для достижения предельно возможного ускорения требуется применять существенно более сложные методы преобразования программ, чем те, которые включаются в традиционные компиляторы.
Для успешного освоения параллельных вычислительных систем пользователям необходимо иметь возможность получать подробные сведения о деталях структуры своих алгоритмов и программ.
Под информационной структурой программы подразумевается совокупность сведений о том, как отдельные элементы программы связаны между собой.
С помощью таких систем можно значительно уменьшить время работы программ на параллельных системах по сравнению со временем, которое показывают те же программы, пропущенные через штатный компилятор. Ускорение в несколько раз удается получить, даже если программы предварительно оптимизируются вручную.
Для достижения предельно возможного ускорения требуется применять существенно более сложные методы преобразования программ, чем те, которые включаются в традиционные компиляторы.
Для успешного освоения параллельных вычислительных систем пользователям необходимо иметь возможность получать подробные сведения о деталях структуры своих алгоритмов и программ.
Под информационной структурой программы подразумевается совокупность сведений о том, как отдельные элементы программы связаны между собой.
Слайд 4Информационная структура программ (4)
Для исследования тонкой информационной структуры программ используются графовые
модели, формализующие отдельные срабатывания операторов и точное описание информационных связей.
Автоматизированный разбор исследуемой программы состоит в анализе каждого оператора и представлении информации об его информационных связях с другими фрагментами программы в виде совокупности графовых структур.
Далее, уже в терминах теории графов, проводится компьютерный анализ независимости отдельных фрагментов программы.
Методы анализа программ основаны на проверке некоторого набора достаточных условий информационной независимости друг от друга отдельных фрагментов исследуемого кода. Найденные свойства используются для адаптации (автоматического преобразования) программ с ориентацией на конкретную архитектуру. НО:
Нет гарантии, что программа действительно не обладает нужным свойством, если проверяемое достаточное условие не выполнено.
Новые архитектуры существенно опережают выпуск систем анализа
Автоматизированный разбор исследуемой программы состоит в анализе каждого оператора и представлении информации об его информационных связях с другими фрагментами программы в виде совокупности графовых структур.
Далее, уже в терминах теории графов, проводится компьютерный анализ независимости отдельных фрагментов программы.
Методы анализа программ основаны на проверке некоторого набора достаточных условий информационной независимости друг от друга отдельных фрагментов исследуемого кода. Найденные свойства используются для адаптации (автоматического преобразования) программ с ориентацией на конкретную архитектуру. НО:
Нет гарантии, что программа действительно не обладает нужным свойством, если проверяемое достаточное условие не выполнено.
Новые архитектуры существенно опережают выпуск систем анализа
Слайд 5Информационная структура программ (5)
В системе V-Ray (разработка лаборатории Параллельных информацион-ных технологий
НИВЦ МГУ) реализован более общий подход к анализу программ. В работах В.В.Воеводина и Вл.В.Воеводина сформулированы и доказаны необходимые и достаточные условия существования информационной зависимости в программах.
Эти критерии применимы к широкому классу программ, называемому линейным классом (к каноническому линейному виду может быть приведено на практике большинство программ):
Любое число переменных
Управление при использовании условных операторов и т.п. всегда передается вниз по тексту.
Нет побочных выходов из циклов.
Шаг в цикле всегда +1
Условие передачи управления всегда задается линейными формами по параметрам циклов и входным данным
Входные данные известны в момент запуска программы.
Эти критерии применимы к широкому классу программ, называемому линейным классом (к каноническому линейному виду может быть приведено на практике большинство программ):
Любое число переменных
Управление при использовании условных операторов и т.п. всегда передается вниз по тексту.
Нет побочных выходов из циклов.
Шаг в цикле всегда +1
Условие передачи управления всегда задается линейными формами по параметрам циклов и входным данным
Входные данные известны в момент запуска программы.
Слайд 6Граф алгоритма (1)
Любой компьютерный код описывает семейство алгоритмов, которое определяется входными
данными. Фиксированный набор входных данных однозначно определяет конкретный алгоритм даже при наличии условных операторов, т.к. выбор конкретной реализации определяется тем, как срабатывают условные операторы, а это, в свою очередь, строго зависит от входных данных.
Поэтому последовательный компьютер всегда выполняет некоторую последовательность действий, которая однозначно определена программой и входными данными. Тем самым, однозначно определен результат.
На параллельных системах возможны варианты. В каждый момент времени может выполняться целый набор операций, не зависящих друг от друга. На любой конкретной параллельной системе программа и входные данные однозначно определяют как набор, так и последо-вательность их выполнения. Но сами наборы и порядок их выполнения на разных системах могут быть разными. Чтобы гарантировать получение однозначного результата, порядок выполнения всей совокупности операций должен подчиняться некоторому условию.
Поэтому последовательный компьютер всегда выполняет некоторую последовательность действий, которая однозначно определена программой и входными данными. Тем самым, однозначно определен результат.
На параллельных системах возможны варианты. В каждый момент времени может выполняться целый набор операций, не зависящих друг от друга. На любой конкретной параллельной системе программа и входные данные однозначно определяют как набор, так и последо-вательность их выполнения. Но сами наборы и порядок их выполнения на разных системах могут быть разными. Чтобы гарантировать получение однозначного результата, порядок выполнения всей совокупности операций должен подчиняться некоторому условию.
Слайд 7Граф алгоритма (2)
Решение любой задачи (и на последовательном, и на параллельном
компьютере) сводится к выполнению последовательности мелких операций с конечным числом аргументов. Аргументами выступают:
входные данные,
результаты выполнения предшествующих операций. В этом случае операция не может начаться раньше, чем будут готовы ее аргументы
Значит, для любых двух операций определена одна из двух возможностей
зафиксирована последовательность операций
констатируется факт, что операции могут быть выполнены независимо, т.е. в любой последовательности либо одновременно.
В последнем случае имеем неоднозначность реализации, т.е. порядка выполнения операций, но при этом любая реализация должна обеспечивать однозначный конечный результат.
Графовая трактовка. Строим ориентированный граф, в вершины которого взаимно-однозначно отображается множество операций программы. Ребра со стрелками соединяют вершины, если одна операция поставляет другой операции свои результаты в качестве аргументов.
входные данные,
результаты выполнения предшествующих операций. В этом случае операция не может начаться раньше, чем будут готовы ее аргументы
Значит, для любых двух операций определена одна из двух возможностей
зафиксирована последовательность операций
констатируется факт, что операции могут быть выполнены независимо, т.е. в любой последовательности либо одновременно.
В последнем случае имеем неоднозначность реализации, т.е. порядка выполнения операций, но при этом любая реализация должна обеспечивать однозначный конечный результат.
Графовая трактовка. Строим ориентированный граф, в вершины которого взаимно-однозначно отображается множество операций программы. Ребра со стрелками соединяют вершины, если одна операция поставляет другой операции свои результаты в качестве аргументов.
Слайд 8Граф алгоритма (3)
Входные данные представлены как начальные операции ввода, в виде
вершин (узлов), не имеющих входных дуг (входные вершины графа)
Каждой операции кода соответствует узел (вершина) графа,
Дуги (ребра) со стрелками - пересылка аргументов и результатов,
Результаты – вершины графа без выходных стрелок
Это граф информационной зависимости реализации алгоритма при фиксированных входных данных. ИЛИ граф алгоритма
Граф алгоритма всегда:
параметризованный (имеет место зависимость от входных данных, размерности массивов и т.д.).
детерминированный (если нет условных операторов) или недетерминированный (если условные операторы присутствуют).
ациклический (в программах реализуются только явные вычисления, т.е. вход никогда не совпадает с выходом).
мультиграф (вершины могут быть связаны несколькими дугами),
ориентированный (стрелки)
Каждой операции кода соответствует узел (вершина) графа,
Дуги (ребра) со стрелками - пересылка аргументов и результатов,
Результаты – вершины графа без выходных стрелок
Это граф информационной зависимости реализации алгоритма при фиксированных входных данных. ИЛИ граф алгоритма
Граф алгоритма всегда:
параметризованный (имеет место зависимость от входных данных, размерности массивов и т.д.).
детерминированный (если нет условных операторов) или недетерминированный (если условные операторы присутствуют).
ациклический (в программах реализуются только явные вычисления, т.е. вход никогда не совпадает с выходом).
мультиграф (вершины могут быть связаны несколькими дугами),
ориентированный (стрелки)
Слайд 9Граф алгоритма (4)
Итак, каждое описание алгоритма порождает ориентированный ациклический мультиграф.
Верно
и обратное. Если задан ориентированный ациклический мультиграф, то его всегда можно рассматривать как граф некоторого алгоритма. Для этого каждой вершине нужно поставить в соответствие любую однозначную операцию, имеющую столько аргументов, сколько дуг входит в вершину графа.
Можно написать программы, реализующие один и тот же алгоритм по-разному – и, соответственно, построить разные графы.
Параллельная форма графа:
каждой вершине соответствует
индекс j=1,2,..sвершин графа) так, что если дуга
идет из вершины с индексом i
в вершину с индексом j, то i
Можно написать программы, реализующие один и тот же алгоритм по-разному – и, соответственно, построить разные графы.
Параллельная форма графа:
каждой вершине соответствует
индекс j=1,2,..s
идет из вершины с индексом i
в вершину с индексом j, то i
Слайд 10Граф алгоритма (5)
Каноническая параллельная форма графа.
Помечаем 1 входные вершины, отбрасываем
их вместе с исходящими из них дугами. Получаем снова ациклический граф, помечаем 2 вершины без дуг, отбрасываем их вместе с исходящими дугами и т.д., пока не будет исчерпан весь граф.
При каждом шаге помечается не менее одной вершины. Значит, число различных индексов не превышает числа вершин.
Совокупность вершин, помеченных одинаковым индексом, составляет ярусы, число вершин в ярусе называется шириной яруса.
Высотой графа называется число ярусов. Максимальная ширина яруса во всем графе называется шириной графа.
(1) Для заданного графа каноническая параллельная форма единственна.
(2) Каноническая параллельная форма графа имеет минимальную высоту и максимальную ширину среди других параллельных форм
(3) Между вершинами одного яруса нет дуг, т.е. операции, соответствую-щие вершинам одного яруса, не зависят друг от друга и могут выполняться параллельно.
При каждом шаге помечается не менее одной вершины. Значит, число различных индексов не превышает числа вершин.
Совокупность вершин, помеченных одинаковым индексом, составляет ярусы, число вершин в ярусе называется шириной яруса.
Высотой графа называется число ярусов. Максимальная ширина яруса во всем графе называется шириной графа.
(1) Для заданного графа каноническая параллельная форма единственна.
(2) Каноническая параллельная форма графа имеет минимальную высоту и максимальную ширину среди других параллельных форм
(3) Между вершинами одного яруса нет дуг, т.е. операции, соответствую-щие вершинам одного яруса, не зависят друг от друга и могут выполняться параллельно.
Слайд 11Граф алгоритма (6)
Эквивалентные преобразования графа отражают разные возможности реализации одного и
того же алгоритма. Если реализация последова-тельная, то говорят, что граф упорядочен линейно, его ширина равна 1.
Пусть алгоритм, описываемый графом канонической формы, реализуется на параллельном компьютере в предположении, что
одна операция (вершина) выполняется за одну единицу времени.
Пренебрегаем всеми накладными расходами.
Начало – нулевой момент времени.
(1) все операции одного яруса начинают выполняться одновременно,
(2) время окончания работы яруса соответствует его номеру.
(3) число операций в ярусе совпадает с шириной яруса.
(4) Время реализации алгоритма равно числу ярусов.
Можно отследить зависимость времени реализации алгоритма от ширины графа. ⇒ Графовая модель алгоритма позволяет выявить потенциал параллелизма в соответствующей ему программе.
Поэтому граф можно считать информационным ядром алгоритма.
Зачем все это:
Зная граф алгоритма и его формы – можно понять, каков запас параллелизма в алгоритме и как его лучше реализовать на конкретном компьютере.
Можно применить теорию графов для поиска закономерностей.
Операции построения и преобразования графов программ в принципе можно автоматизировать, тем самым открываются возможности автоматического распараллеливания последовательных кодов, накопленных в библиотеках программ. Вручную этого сделать невозможно. Такая работа проводится в НИВЦ МГУ.
Алгоритм должен иметь параллельную форму, ширина ярусов которой в среднем соответствует числу устройств вычислительной системы.
В общем случае, чем больше ярусов, ширина которых равна числу независимых устройств, тем выше реальная производительность системы на данном алгоритме.
Пусть алгоритм, описываемый графом канонической формы, реализуется на параллельном компьютере в предположении, что
одна операция (вершина) выполняется за одну единицу времени.
Пренебрегаем всеми накладными расходами.
Начало – нулевой момент времени.
(1) все операции одного яруса начинают выполняться одновременно,
(2) время окончания работы яруса соответствует его номеру.
(3) число операций в ярусе совпадает с шириной яруса.
(4) Время реализации алгоритма равно числу ярусов.
Можно отследить зависимость времени реализации алгоритма от ширины графа. ⇒ Графовая модель алгоритма позволяет выявить потенциал параллелизма в соответствующей ему программе.
Поэтому граф можно считать информационным ядром алгоритма.
Зачем все это:
Зная граф алгоритма и его формы – можно понять, каков запас параллелизма в алгоритме и как его лучше реализовать на конкретном компьютере.
Можно применить теорию графов для поиска закономерностей.
Операции построения и преобразования графов программ в принципе можно автоматизировать, тем самым открываются возможности автоматического распараллеливания последовательных кодов, накопленных в библиотеках программ. Вручную этого сделать невозможно. Такая работа проводится в НИВЦ МГУ.
Алгоритм должен иметь параллельную форму, ширина ярусов которой в среднем соответствует числу устройств вычислительной системы.
В общем случае, чем больше ярусов, ширина которых равна числу независимых устройств, тем выше реальная производительность системы на данном алгоритме.
Слайд 12Граф алгоритма (7)
Выводы (зачем это все надо)
Зная граф алгоритма и его
формы – можно оценить запас параллелизма в алгоритме и то, как его лучше реализовать на конкретном компьютере.
Можно применить теорию графов для поиска закономерностей.
Операции построения и преобразования графов программ в принципе можно автоматизировать, тем самым открываются возможности автоматического распараллеливания последовательных кодов, накопленных в библиотеках программ. Вручную этого сделать невозможно.
Алгоритм должен иметь параллельную форму, ширина ярусов которой в среднем соответствует числу устройств вычислительной системы.
В общем случае, чем больше ярусов, ширина которых равна числу независимых устройств, тем выше реальная производительность системы на данном алгоритме.
Можно применить теорию графов для поиска закономерностей.
Операции построения и преобразования графов программ в принципе можно автоматизировать, тем самым открываются возможности автоматического распараллеливания последовательных кодов, накопленных в библиотеках программ. Вручную этого сделать невозможно.
Алгоритм должен иметь параллельную форму, ширина ярусов которой в среднем соответствует числу устройств вычислительной системы.
В общем случае, чем больше ярусов, ширина которых равна числу независимых устройств, тем выше реальная производительность системы на данном алгоритме.
Слайд 13Граф алгоритма (8)
Рассмотрим идею построения алгоритмов малой высоты на примере вычисления
умножения n чисел. Пусть n=8.
Последовательное умножение. Данные: а1, а2, а3, а4, а5, а6, а7, а8
Ярус 1: а1*а2
Ярус 2: (а1*а2) * а3
Ярус 3: (а1*а2*а3) * а4
Ярус 4: (а1*а2*а3*а4) * а5
Ярус 5: (а1*а2*а3*а4*а5) * а6
Ярус 6: (а1*а2*а3*а4*а5*а6) * а7
Ярус 7: (а1*а2*а3*а4*а5*а6*а7) * а8
Ввод 1 2 3 4 5 6 7
Высота параллельной формы алгоритма 7, ширина 1.
Последовательное умножение. Данные: а1, а2, а3, а4, а5, а6, а7, а8
Ярус 1: а1*а2
Ярус 2: (а1*а2) * а3
Ярус 3: (а1*а2*а3) * а4
Ярус 4: (а1*а2*а3*а4) * а5
Ярус 5: (а1*а2*а3*а4*а5) * а6
Ярус 6: (а1*а2*а3*а4*а5*а6) * а7
Ярус 7: (а1*а2*а3*а4*а5*а6*а7) * а8
Ввод 1 2 3 4 5 6 7
Высота параллельной формы алгоритма 7, ширина 1.
Если в вычислительной системе больше 1 процессора – остальные на всех шагах будут простаивать.
Слайд 14Граф алгоритма (9)
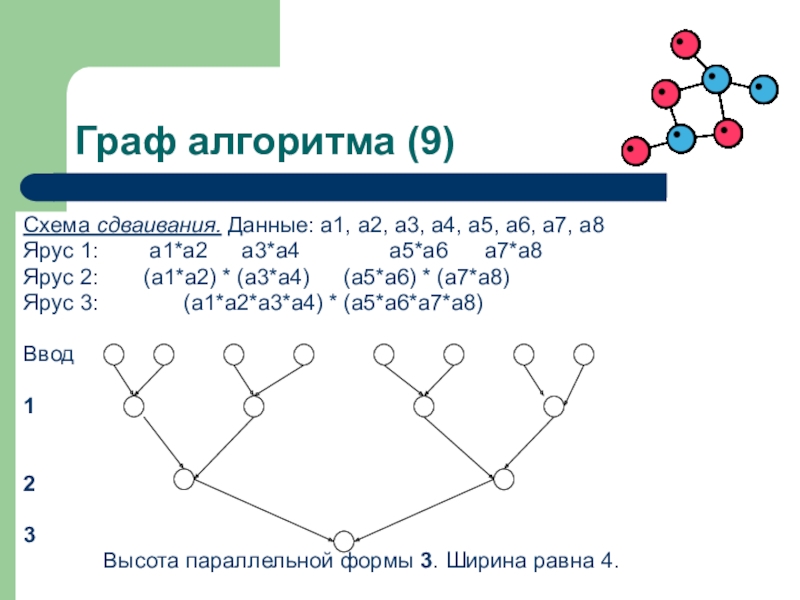
Схема сдваивания. Данные: а1, а2, а3, а4, а5, а6,
а7, а8
Ярус 1: а1*а2 а3*а4 а5*а6 а7*а8
Ярус 2: (а1*а2) * (а3*а4) (а5*а6) * (а7*а8)
Ярус 3: (а1*а2*а3*а4) * (а5*а6*а7*а8)
Ввод
1
2
3
Высота параллельной формы 3. Ширина равна 4.
Ярус 1: а1*а2 а3*а4 а5*а6 а7*а8
Ярус 2: (а1*а2) * (а3*а4) (а5*а6) * (а7*а8)
Ярус 3: (а1*а2*а3*а4) * (а5*а6*а7*а8)
Ввод
1
2
3
Высота параллельной формы 3. Ширина равна 4.
Слайд 15Граф алгоритма (10)
Существенное снижение высоты произошло за счет более полной загруженности
процессоров выполнением полезной работы (хотя загруженность уменьшается от яруса к ярусу, это минус).
В общем случае алгоритм реализуется на [n/2] процессорах, высота составляет [log2(n)] (квадратные скобки означают ближайшее сверху целое число).
С помощью процесса сдваивания можно строить алгоритмы логарифми-ческой высоты для любой ассоциативной операции (+, MIN, MAX, и т.п.)
Концепция неограниченного параллелизма получила развитие в 60е.
Цель – построение алгоритмов минимальной высоты, т.к. именно высота определяет время реализации алгоритмов, если считать, что независимых устройств в параллельной системе сколь угодно много, и пренебречь накладными расходами.
Идея привлекательна для проведения математических исследований, но большинство алгоритмов на практике оказались неэффективными из-за огромного числа требуемых процессоров и сложных информационных связей между ними («выжило» лишь сдваивание и еще кое-что)
В общем случае алгоритм реализуется на [n/2] процессорах, высота составляет [log2(n)] (квадратные скобки означают ближайшее сверху целое число).
С помощью процесса сдваивания можно строить алгоритмы логарифми-ческой высоты для любой ассоциативной операции (+, MIN, MAX, и т.п.)
Концепция неограниченного параллелизма получила развитие в 60е.
Цель – построение алгоритмов минимальной высоты, т.к. именно высота определяет время реализации алгоритмов, если считать, что независимых устройств в параллельной системе сколь угодно много, и пренебречь накладными расходами.
Идея привлекательна для проведения математических исследований, но большинство алгоритмов на практике оказались неэффективными из-за огромного числа требуемых процессоров и сложных информационных связей между ними («выжило» лишь сдваивание и еще кое-что)
Слайд 16Графовые модели программ (1)
Не совсем то, что граф алгоритма, хотя, конечно,
эти понятия взаимосвязаны. Существуют разные классы графовых моделей программ. Цели:
- изучение информационной структуры программы на уровне отдельных операций.
- необходимость научиться по тексту программы как можно точнее определить информационные связи между отдельными операциями.
- выявление потенциала параллелизма и путей оптимизации программы.
Создаются модели как отдельных подпрограмм или отдельных блоков программ, так и модели больших составных программ (граф вызовов процедур, граф использования общей памяти и др).
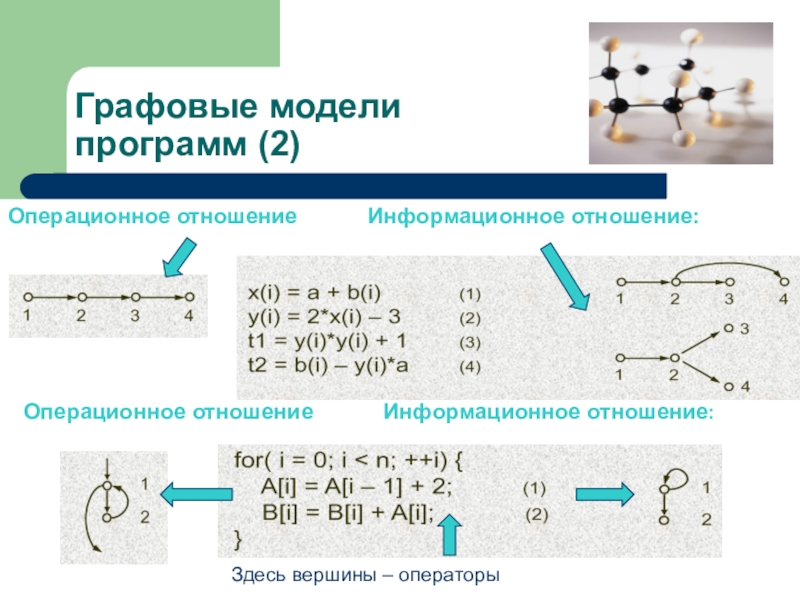
Вершинами графа могут выступать операторы, циклы, линейные участки программ, вызовы процедур и др. Дуги отражают связь (отношение) между вершинами
Операционное: Две вершины A и B соединяются направленной дугой тогда и только тогда, когда вершина B может быть выполнена сразу после вершины A.
Информационное: Две вершины A и B соединяются направленной дугой тогда и только тогда, когда вершина В использует в качестве аргумента некоторое значение, полученное в вершине A.
- изучение информационной структуры программы на уровне отдельных операций.
- необходимость научиться по тексту программы как можно точнее определить информационные связи между отдельными операциями.
- выявление потенциала параллелизма и путей оптимизации программы.
Создаются модели как отдельных подпрограмм или отдельных блоков программ, так и модели больших составных программ (граф вызовов процедур, граф использования общей памяти и др).
Вершинами графа могут выступать операторы, циклы, линейные участки программ, вызовы процедур и др. Дуги отражают связь (отношение) между вершинами
Операционное: Две вершины A и B соединяются направленной дугой тогда и только тогда, когда вершина B может быть выполнена сразу после вершины A.
Информационное: Две вершины A и B соединяются направленной дугой тогда и только тогда, когда вершина В использует в качестве аргумента некоторое значение, полученное в вершине A.
Слайд 17Графовые модели программ (2)
Операционное отношение Информационное отношение:
Здесь вершины – операторы
Операционное отношение Информационное отношение:
Слайд 18Графовые модели программ (3)
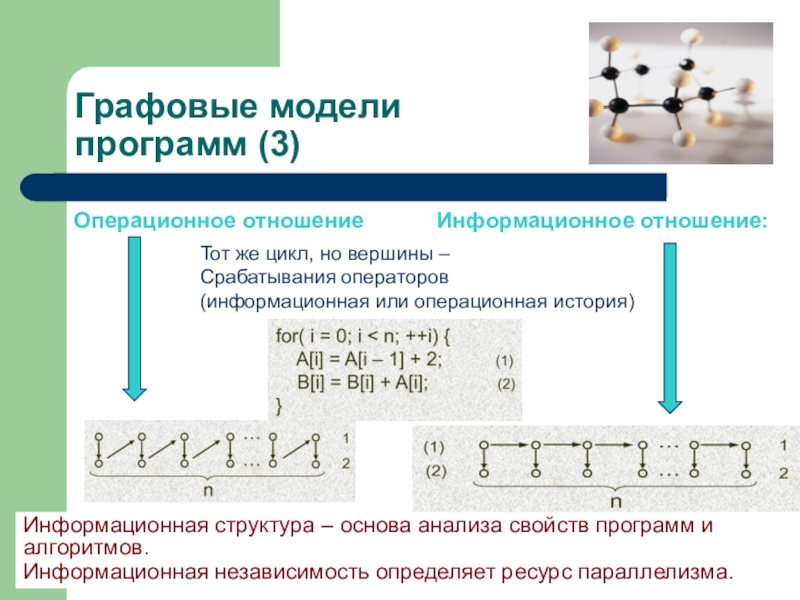
Тот же цикл, но вершины –
Срабатывания операторов
(информационная
или операционная история)
Операционное отношение Информационное отношение:
Информационная структура – основа анализа свойств программ и алгоритмов.
Информационная независимость определяет ресурс параллелизма.
Слайд 19Графовые модели программ (4)
Параллельная структура программы – совокупность сведений о парал-лельных
множествах в пространстве итераций и о преобразованиях, с помощью которых выявляются параллельные множества.
Знание параллельной структуры программы дает возможность выявить пути ее эффективной параллельной реализации в зависимости от архитектуры вычислительной системы.
Знание структуры программ может помочь выявить типичные вычислительные блоки с тем, чтобы максимально адаптировать архитектуру вычислительных систем под конкретные требования, связанные с определенным классом задач.
Множества вершин графа зависимостей называются параллельными,
если любой путь графа, связывающий две вершины, принадлежит этому множеству,
если никакие две вершины из разных множеств не связаны путем.
Макропараллелизм – в параллельном множестве много точек.
Микропараллелизм – много параллельных множеств с малым числом точек.
Знание параллельной структуры программы дает возможность выявить пути ее эффективной параллельной реализации в зависимости от архитектуры вычислительной системы.
Знание структуры программ может помочь выявить типичные вычислительные блоки с тем, чтобы максимально адаптировать архитектуру вычислительных систем под конкретные требования, связанные с определенным классом задач.
Множества вершин графа зависимостей называются параллельными,
если любой путь графа, связывающий две вершины, принадлежит этому множеству,
если никакие две вершины из разных множеств не связаны путем.
Макропараллелизм – в параллельном множестве много точек.
Микропараллелизм – много параллельных множеств с малым числом точек.
Слайд 23Графовые модели программ (8): эквивалентные преобразования
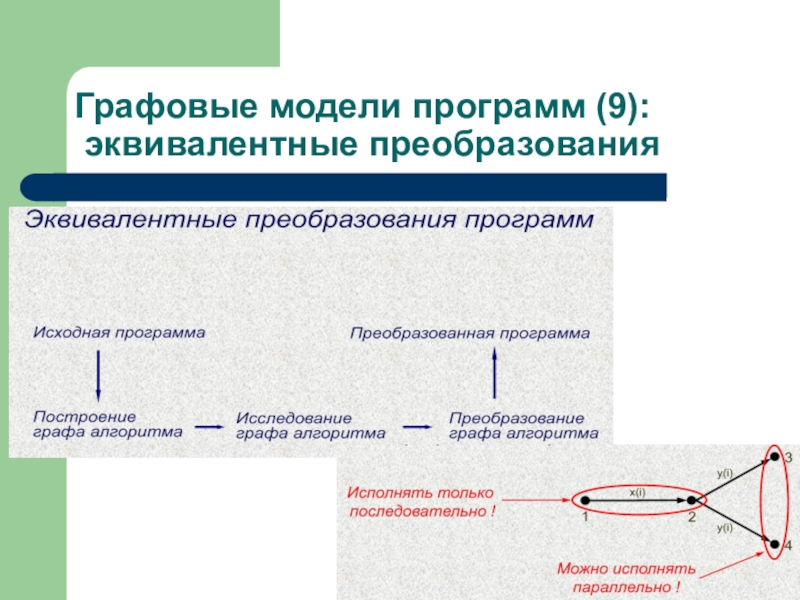
Один и тот же алгоритм можно
записать разными способами, но важно чтобы результат при одинаковых входных данных был одинаковым. Поэтому вводится понятие эквивалентности программ и эквивалентных преобразований программ и графов (строго, в терминах теории графов). Эквивалентные программы при последовательной реализации на одних и тех же входных данных дают одну и ту же последовательность результатов, включая ошибки округления.
Примеры наиболее распространенных эквивалентных преобразований
перестановка циклов
слияние циклов
распределение циклов (процедура, обратная слиянию)
переупорядочивание операторов
расщепление итераций
обратный порядок итераций
выделение стандартных операций
треугольные преобразования цикла, скашивание
Примеры наиболее распространенных эквивалентных преобразований
перестановка циклов
слияние циклов
распределение циклов (процедура, обратная слиянию)
переупорядочивание операторов
расщепление итераций
обратный порядок итераций
выделение стандартных операций
треугольные преобразования цикла, скашивание