- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Информатика Арифметические и логические основы работы компьютера
Содержание
- 1. Информатика Арифметические и логические основы работы компьютера
- 2. АРИФМЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ ЭВМ
- 3. Например
- 4. Алгебра логикиАлгебра логики (булева алгебра) – это
- 5. понятие, суждение, умозаключение; доказательствоЛогика состоит из форм
- 6. это форма мышления, отражающая наиболее существенные свойства
- 7. равнозначность, когда объемы понятий полностью совпадают; пересечение,
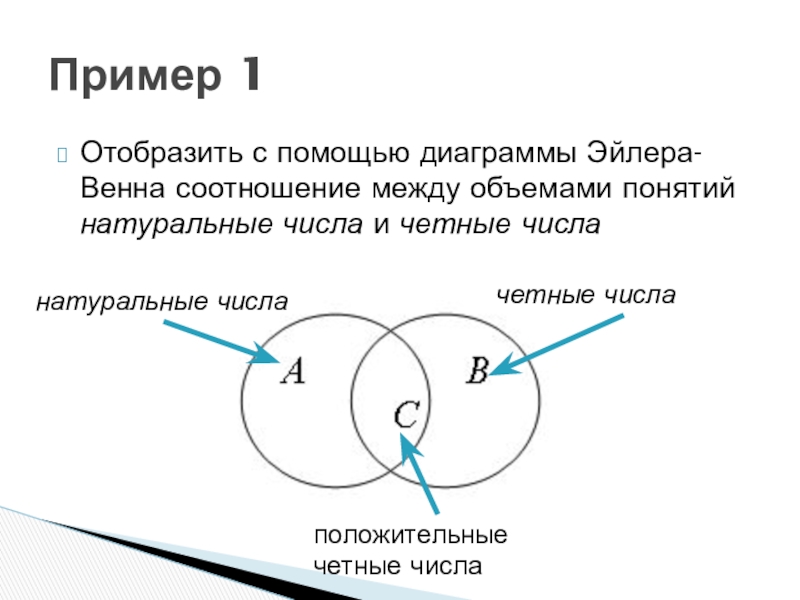
- 8. Отобразить с помощью диаграммы Эйлера-Венна соотношение между
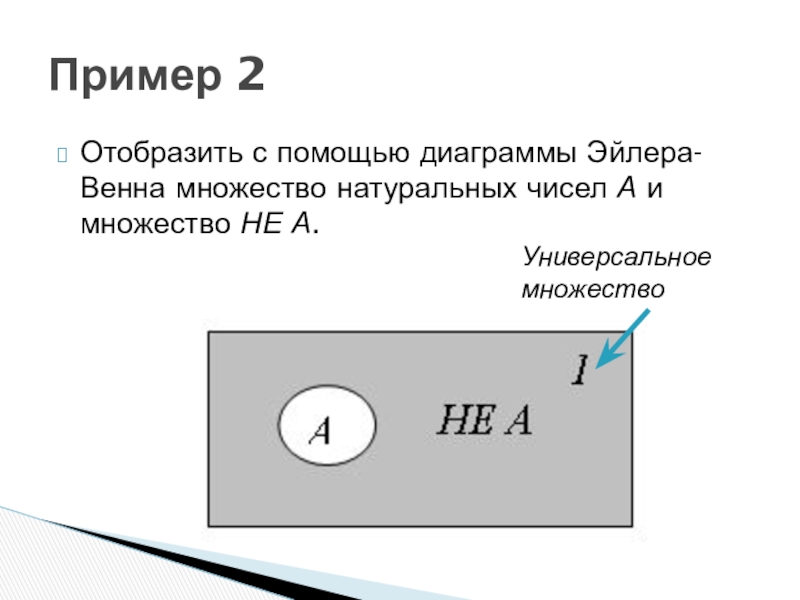
- 9. Отобразить с помощью диаграммы Эйлера-Венна множество натуральных чисел А и множество НЕ А.Пример 2Универсальное множество
- 10. - это форма мышления, выраженная с помощью
- 11. Высказывание называется простым, если никакая его часть
- 12. Понятие о предмете мысли называется субъектом и
- 13. Определить, что в суждении «Компьютер состоит из
- 14. предикат от n переменных (от n неопределенных
- 15. В вышеописанных предикатах заменить неопределенные термины на
- 16. это форма мышления, посредством которой из одного
- 17. Например, из двух суждений: «Все металлы электропроводны»
- 18. Например, установив, что отдельные металлы - железо,
- 19. Доказательство есть мыслительный процесс, направленный на подтверждение
- 20. Простые высказывания в алгебре логики обозначаются заглавными
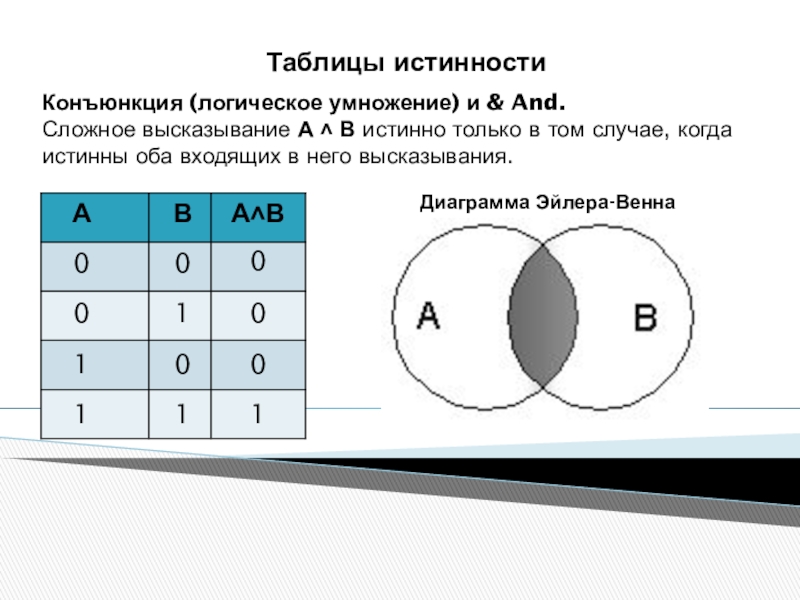
- 21. Таблицы истинностиКонъюнкция (логическое умножение) и & And.
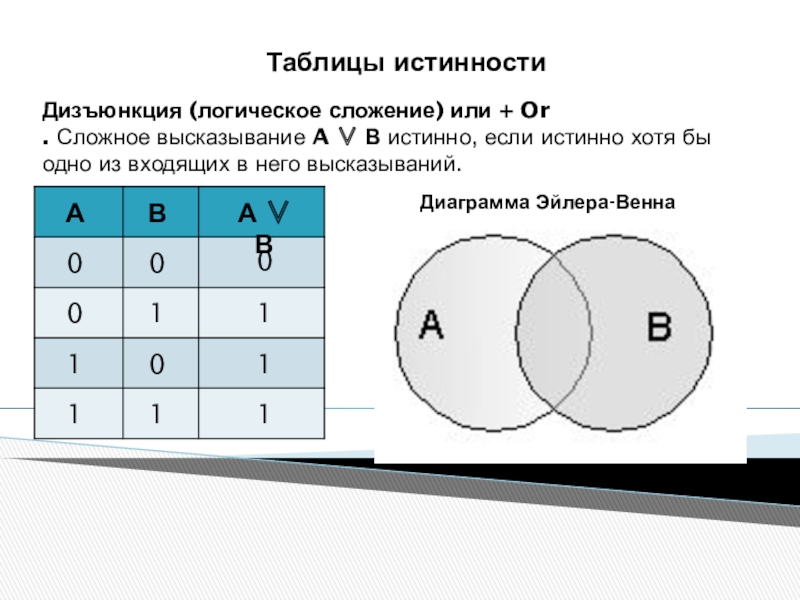
- 22. Таблицы истинностиДизъюнкция (логическое сложение) или + Or.
- 23. Таблицы истинностиИнверсия (логическое отрицание). Присоединение частицы НЕ
- 24. Импликация - это логическая операция, ставящая в
- 25. это логическая операция, ставящая в соответствие каждым
- 26. действия в скобках;инверсия;конъюнкция;дизъюнкция и строгая дизъюнкция;импликация;эквивалентность.В логических выражениях операции имеют следующий приоритет:
- 27. Законы алгебры логики
Слайд 4Алгебра логики
Алгебра логики
(булева алгебра) –
это раздел математики, возникший в
Слайд 6это форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от
В структуре каждого понятия две стороны: содержание и объем.
Объем понятия - это совокупность предметов, на которую он распространяется, и может быть представлен в форме множества объектов, состоящий из элементов множества
Понятие
Слайд 7равнозначность, когда объемы понятий полностью совпадают;
пересечение, когда объемы понятий частично
подчинения, когда объем одного понятия полностью входит в объем другого и т.д.
диаграммы Эйлера-Венна
виды отношений между множествами
Слайд 8Отобразить с помощью диаграммы Эйлера-Венна соотношение между объемами понятий натуральные числа
Пример 1
натуральные числа
четные числа
положительные четные числа
Слайд 9Отобразить с помощью диаграммы Эйлера-Венна множество натуральных чисел А и множество
Пример 2
Универсальное множество
Слайд 10- это форма мышления, выраженная с помощью понятий, посредством которой что-либо
высказывание может быть истинным или ложным.
Высказывание (суждение)
Слайд 11Высказывание называется простым, если никакая его часть сама не является высказыванием.
Высказывание, состоящее из простых высказываний, называются составным (сложным).
Слайд 12Понятие о предмете мысли называется субъектом и обозначается буквой S,
понятие
Оба эти понятия - субъект и предикат называются терминами суждения.
логическая форма высказывания
Слайд 13Определить, что в суждении
«Компьютер состоит из процессора, памяти и внешних
является субъектом, предикатом и связкой.
Пример 3
Слайд 14предикат от n переменных (от n неопределенных понятий) выражается формулой:
При n = 1, когда один из терминов является неопределенным понятием, мы имеем предикат первого порядка, например, «х – человек».
При n = 2, когда два термина неопределены, мы имеем предикат второго порядка, например,
«х любит y».
При n = 3, когда неопределенны три термина, мы имеем предикат третьего порядка, например, «z - сын x и y».
Предикат
Слайд 15В вышеописанных предикатах заменить неопределенные термины на конкретные понятия.
Преобразуем предикаты
x = «Сократ»,
y = «Ксантиппа»,
z = «Софрониск»
Пример 4
Слайд 16это форма мышления, посредством которой из одного или нескольких суждений, называемых
Умозаключение
дедуктивные,
индуктивные
Умозаключения бывают
Слайд 17Например, из двух суждений:
«Все металлы электропроводны»
и
«Ртуть является металлом»
Вывод:
В дедуктивных умозаключениях рассуждения ведутся
от общего к частному.
Слайд 18Например,
установив, что отдельные металлы - железо, медь, цинк, алюминий и
можно сделать вывод, что ?
В индуктивных умозаключениях рассуждения ведутся
от частного к общему.
Слайд 19Доказательство есть мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения
Доказательство
Слайд 20Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А =
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному — 0.
Таким образом, А = 1, В = 0.
Алгебра высказываний
Слайд 21Таблицы истинности
Конъюнкция (логическое умножение) и & And.
Сложное высказывание А ˄
А
В
А˄В
0
0
0
0
1
0
1
0
0
1
1
1
Диаграмма Эйлера-Венна
Слайд 22Таблицы истинности
Дизъюнкция (логическое сложение) или + Or
. Сложное высказывание A
А
В
А В
0
0
0
0
1
1
1
0
1
1
1
1
Диаграмма Эйлера-Венна
Слайд 23Таблицы истинности
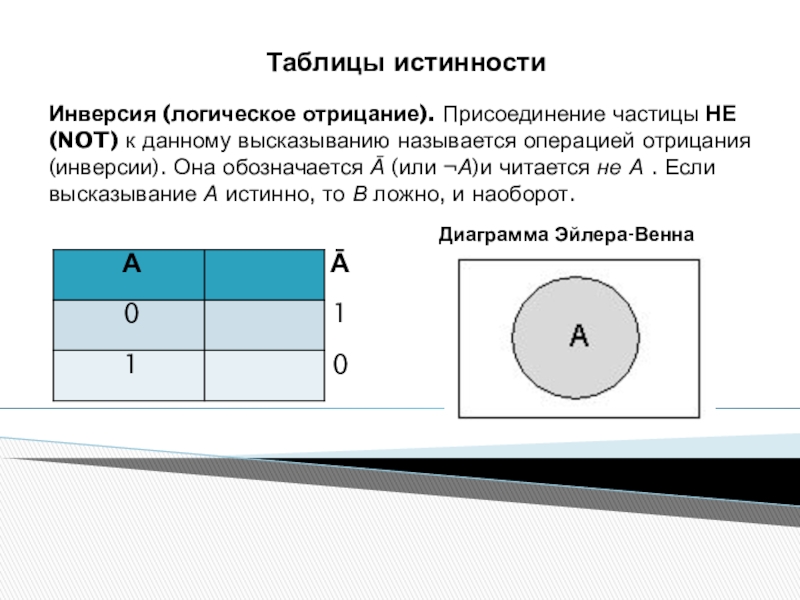
Инверсия (логическое отрицание). Присоединение частицы НЕ (NOT) к данному высказыванию
А
Ā
0
1
1
0
Диаграмма Эйлера-Венна
Слайд 24Импликация - это логическая операция, ставящая в соответствие каждым двум простым
Логическая операция ИМПЛИКАЦИЯ (логическое следование)
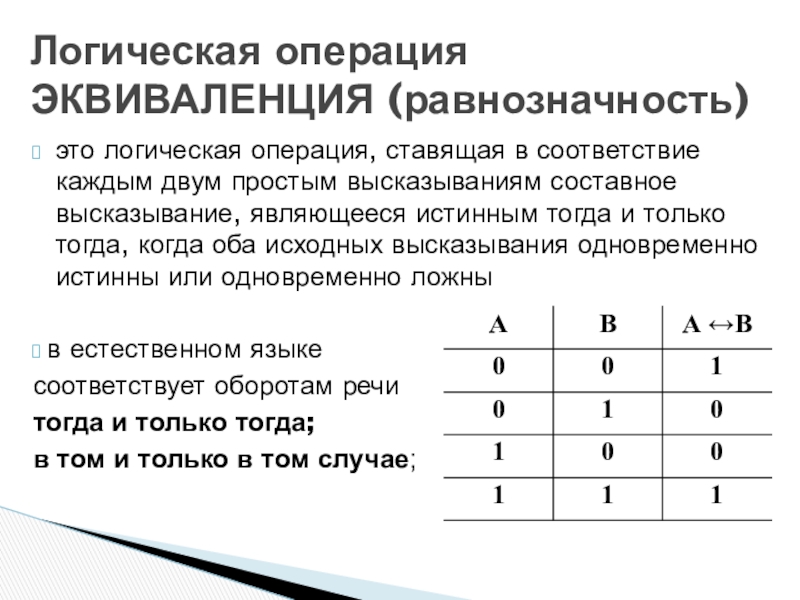
Слайд 25это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное
в естественном языке
соответствует оборотам речи
тогда и только тогда;
в том и только в том случае;
Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность)