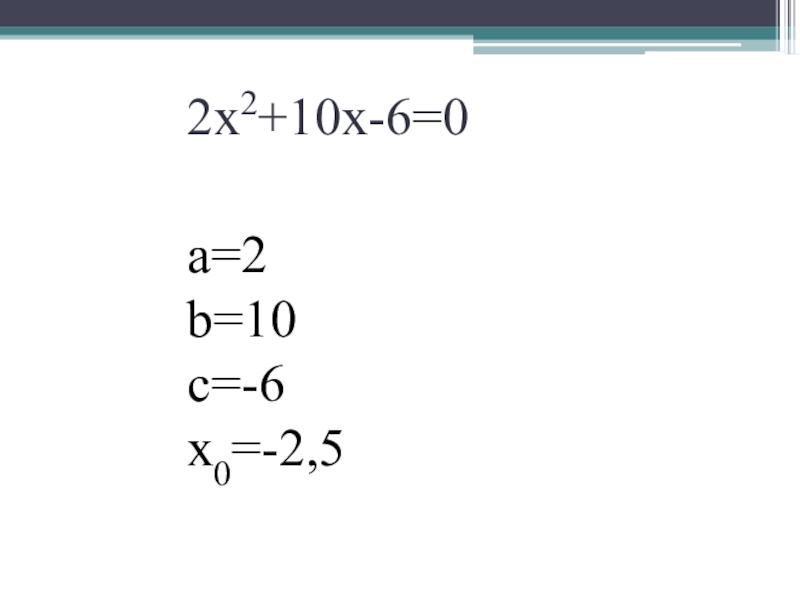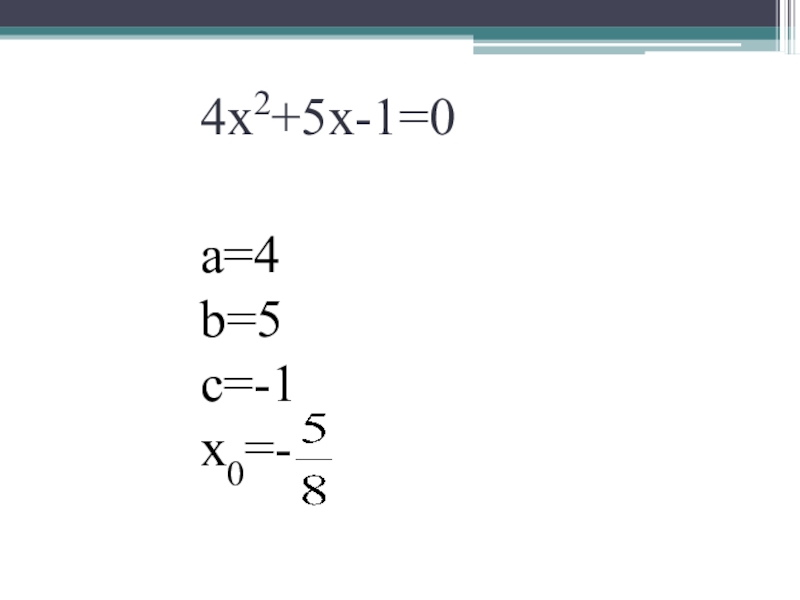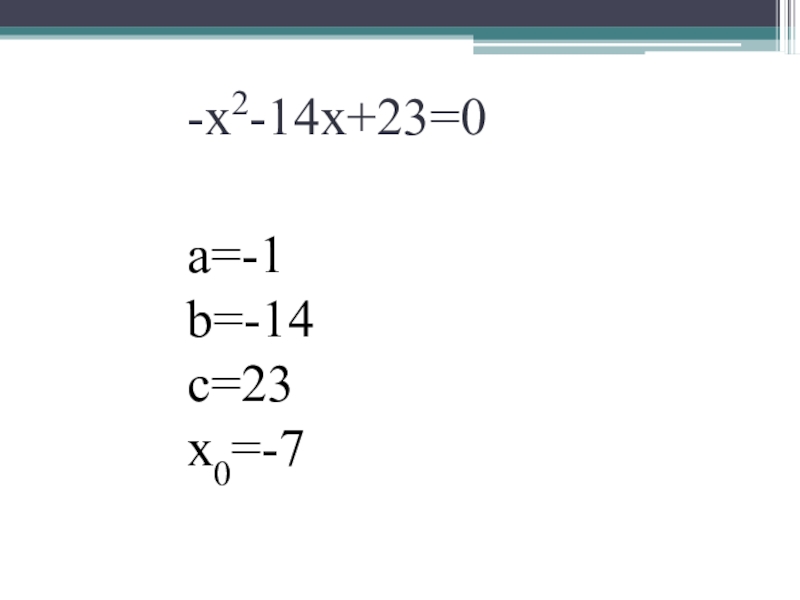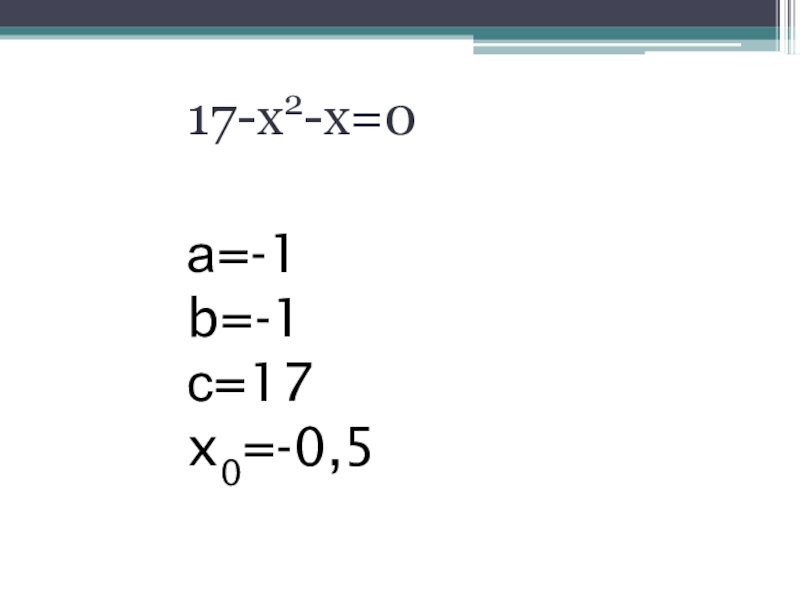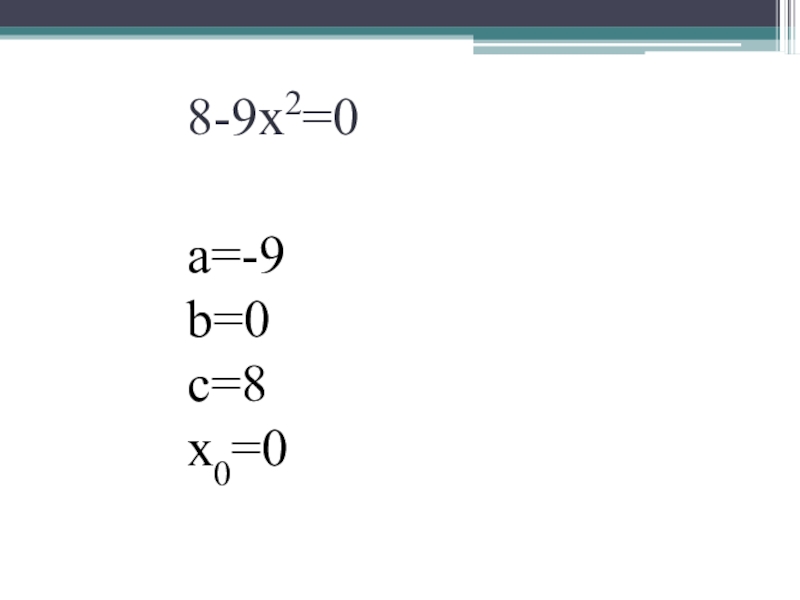Учитель информатики
(по специальности математика и информатика)
Шихмагомедов Эльбрус Асланбекович
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Графический способ решения квадратных уравнений с помощью Excel
Содержание
- 1. Графический способ решения квадратных уравнений с помощью Excel
- 2. Цель урока: Обеспечить умение
- 3. «Дорогу осилит идущий, а информатику –
- 4. «Графический способ решения квадратных уравнений с помощью Excel»Тема урока:
- 5. 2х2+10х-6=0а=2b=10с=-6x0=-2,5
- 6. 4х2+5х-1=0а=4b=5с=-1x0=-
- 7. -х2-14х+23=0а=-1b=-14с=23x0=-7
- 8. 17-х2-х=0а=-1b=-1с=17x0=-0,5
- 9. 8-9х2=0а=-9b=0с=8x0=0
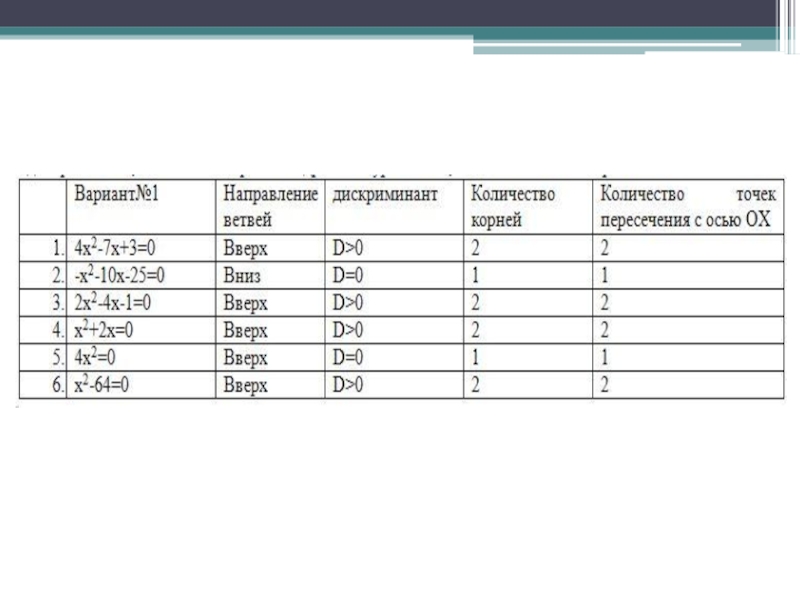
- 10. Определить количество корней в уравнении:Вариант I9y2+6y+1=0;2x2+8x+13=0.Вариант II4y2-4y+1=0;3x2+32x+80=0;Вариант III x2+10x+25=0; 3x2+5x+15=0.
- 11. «Недостойно одаренному человеку, тратить
- 12. Электронные таблицы (ЭТ)1) Для чего предназначены электронные
- 13. Устные упражнения (по информатике)Какой вид примет содержащая
- 14. 3. Дан фрагмент электронной таблицы: В ячейку D2
- 15. 4. Дан фрагмент электронной таблицы: В ячейку D1
- 16. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс.
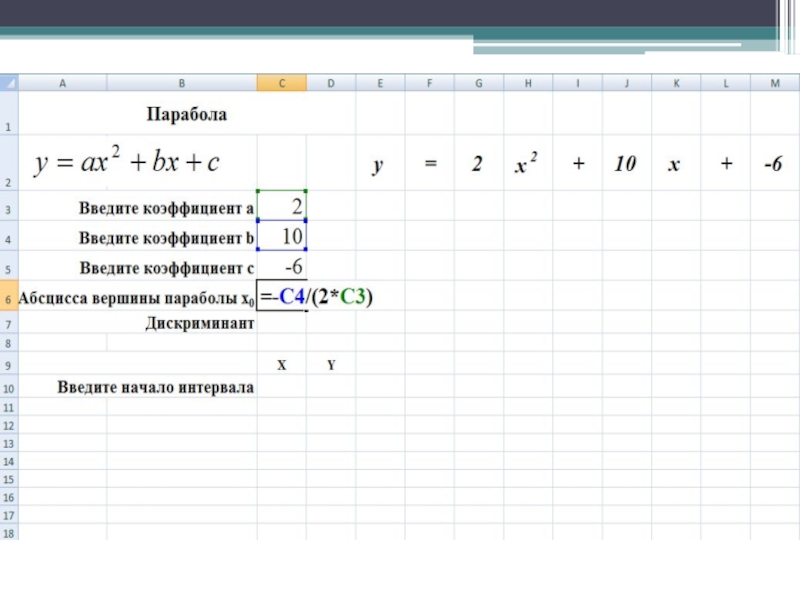
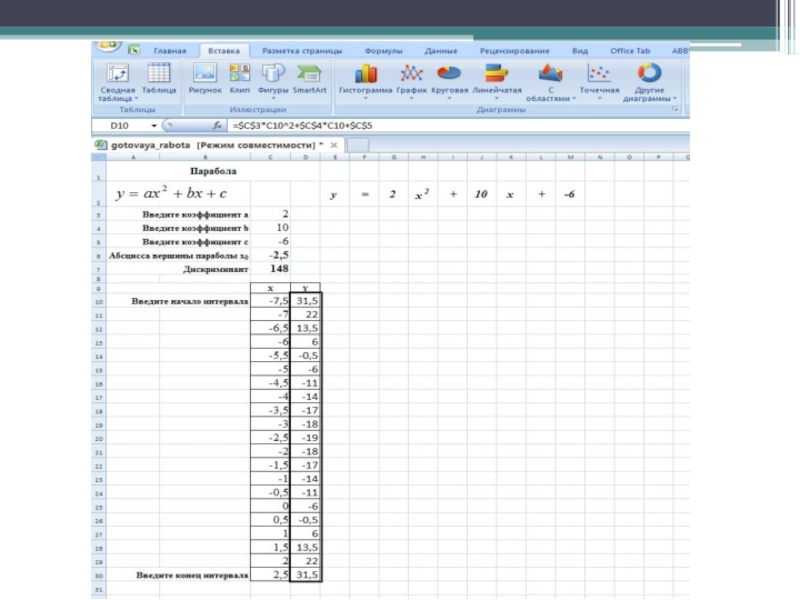
- 17. Решим квадратное уравнение 2x2+10x-6=0. Для этого
- 18. Слайд 18
- 19. Слайд 19
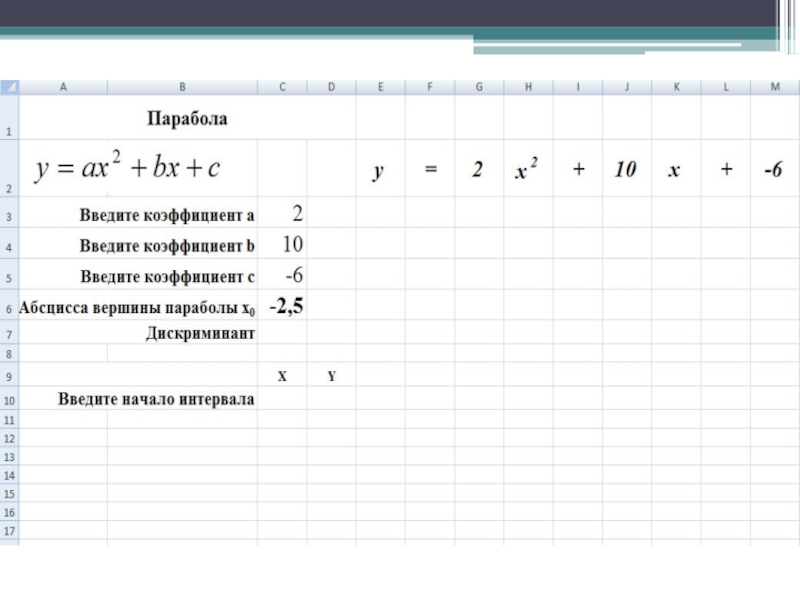
- 20. Найдите координаты вершины параболы x0=-b/(2*a);
- 21. Слайд 21
- 22. Слайд 22
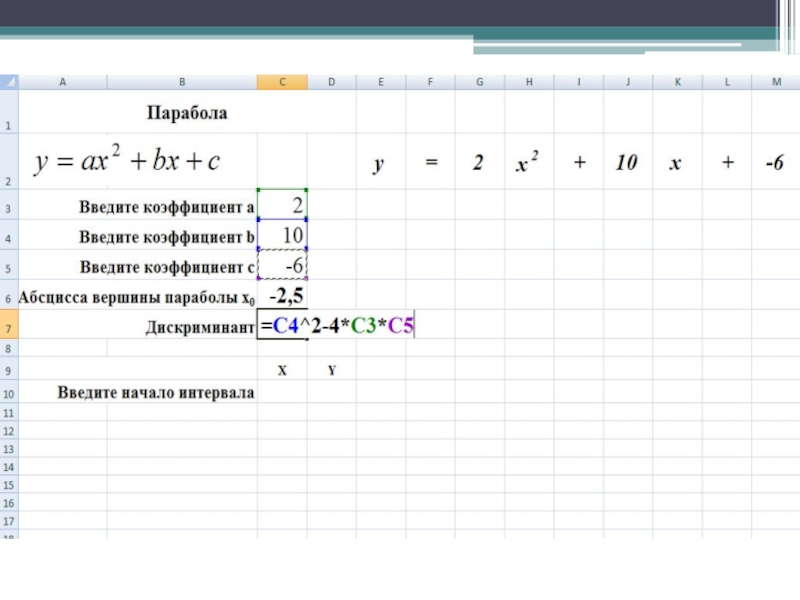
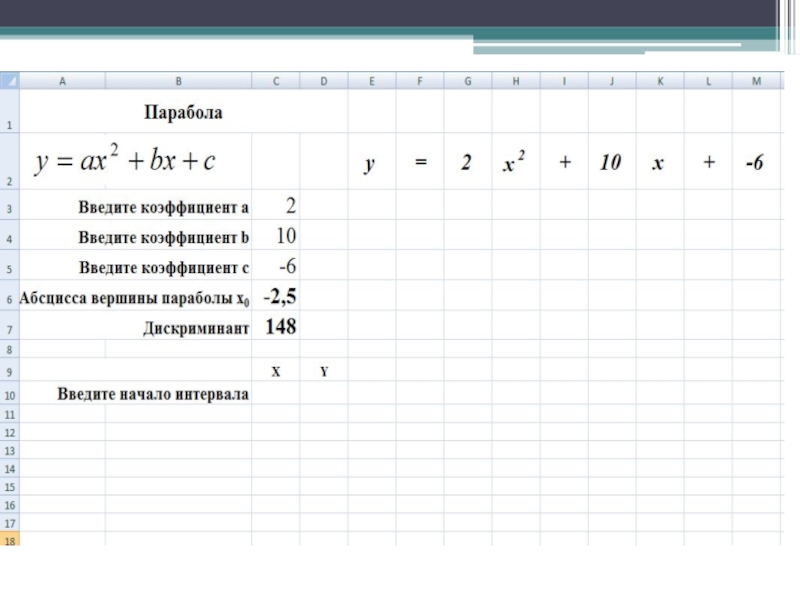
- 23. Найдите дискриминант=b^2 – 4*a*c
- 24. Слайд 24
- 25. Слайд 25
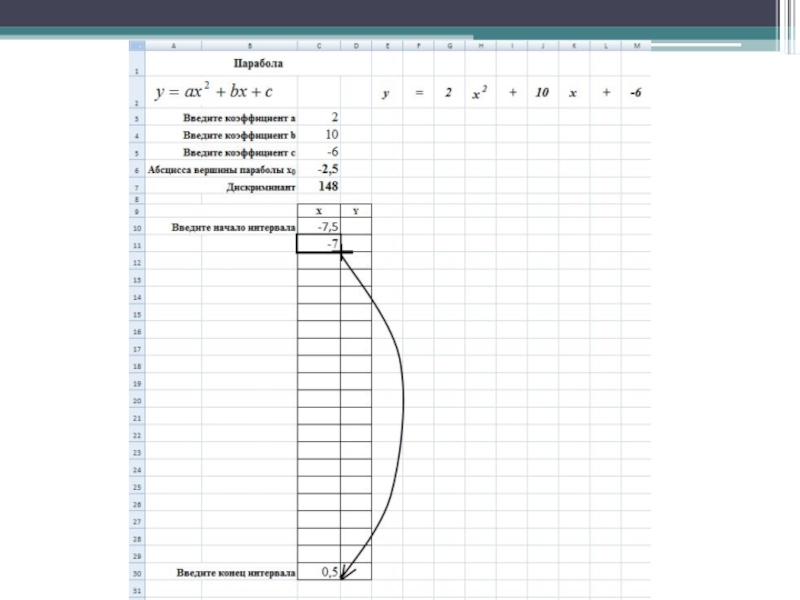
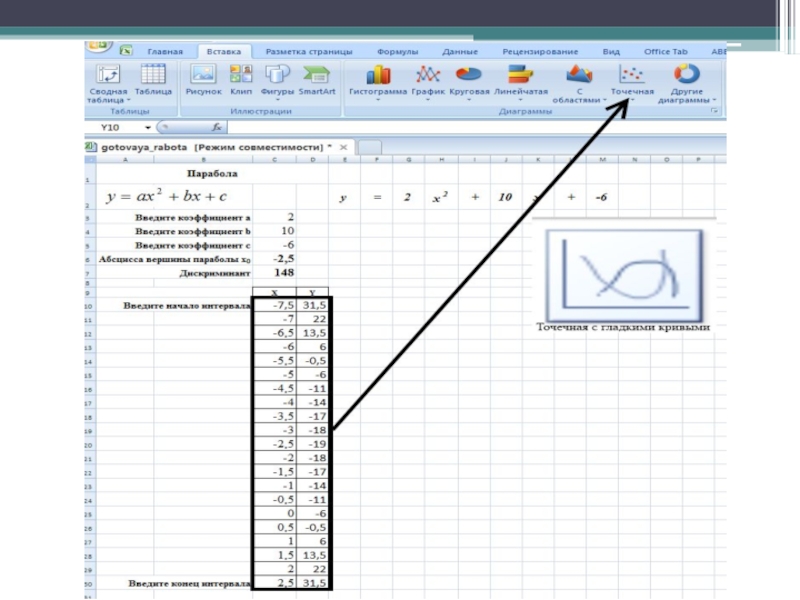
- 26. Введите начало интервала
- 27. Введите конец интервала
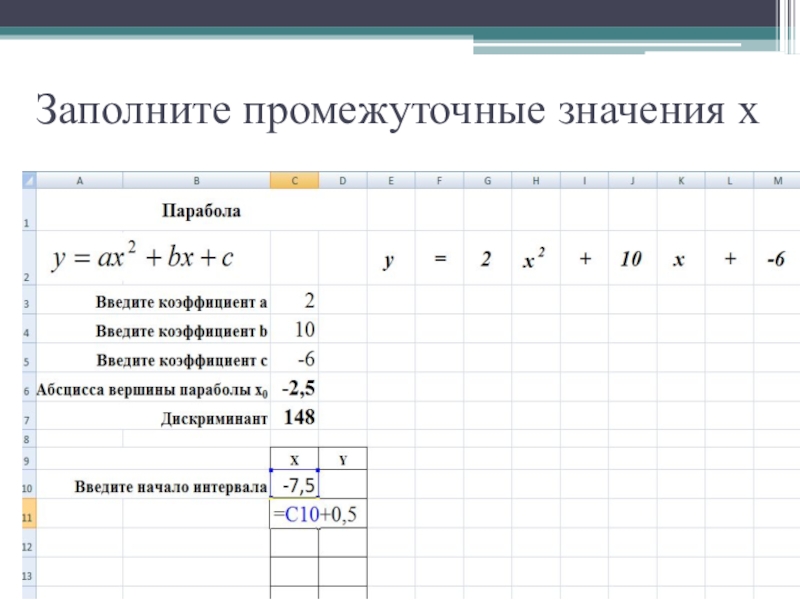
- 28. Заполните промежуточные значения х
- 29. Слайд 29
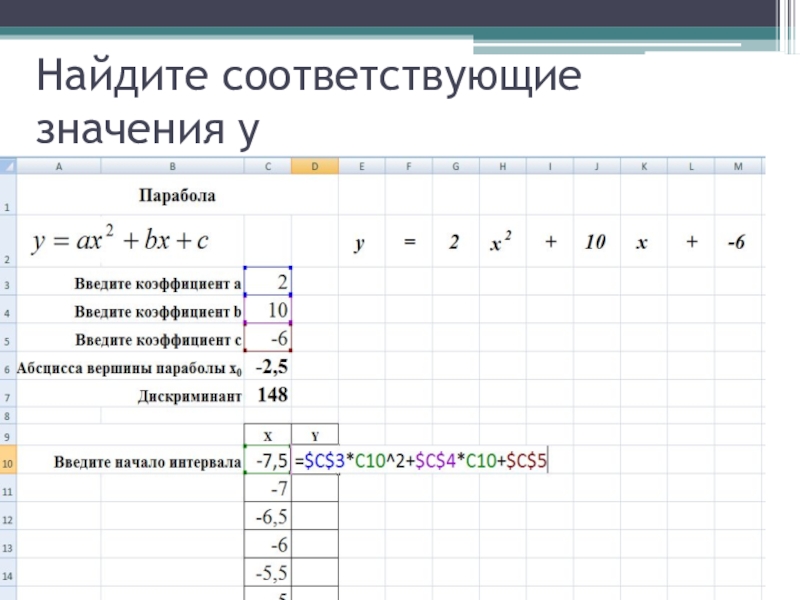
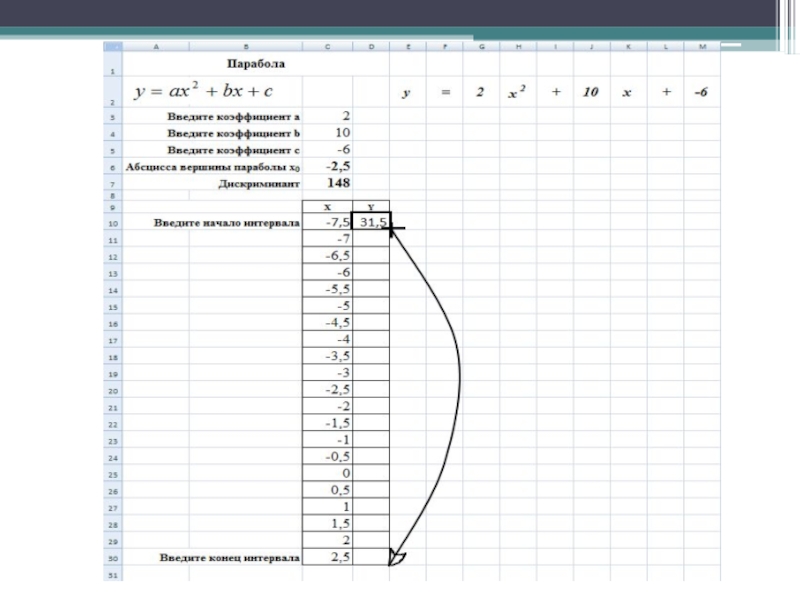
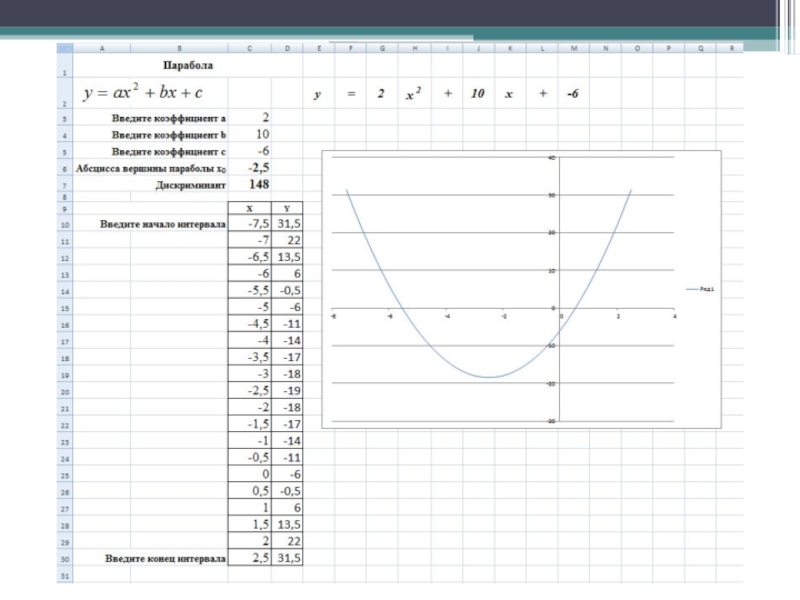
- 30. Найдите соответствующие значения у
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Физминутка«Здоровье - не все, но все без
- 36. Самостоятельная работа
- 37. Слайд 37
- 38. РефлексияКак может располагаться парабола относительно оси x?
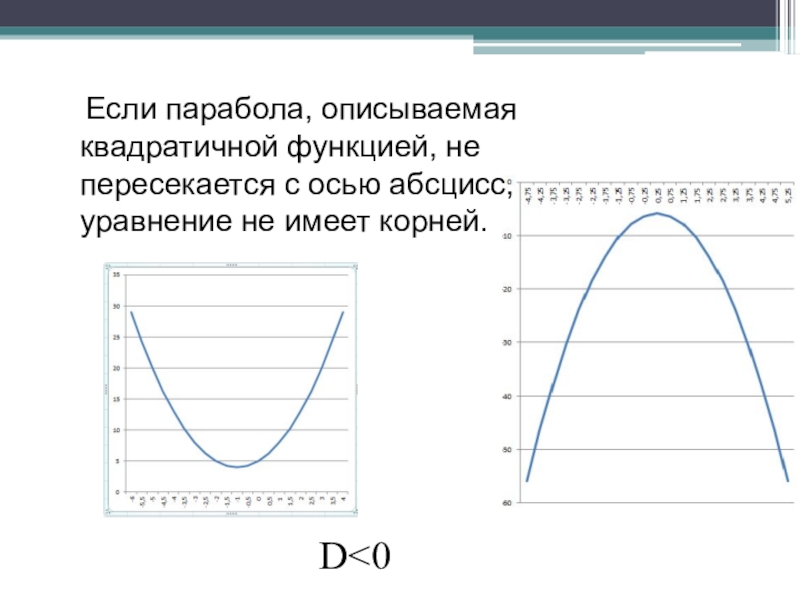
- 39. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет корней. D
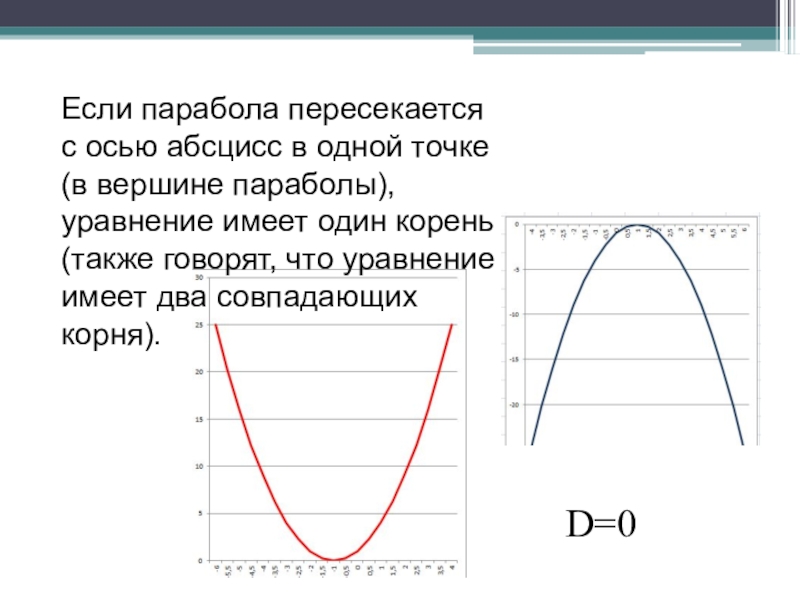
- 40. Если парабола пересекается с осью абсцисс в
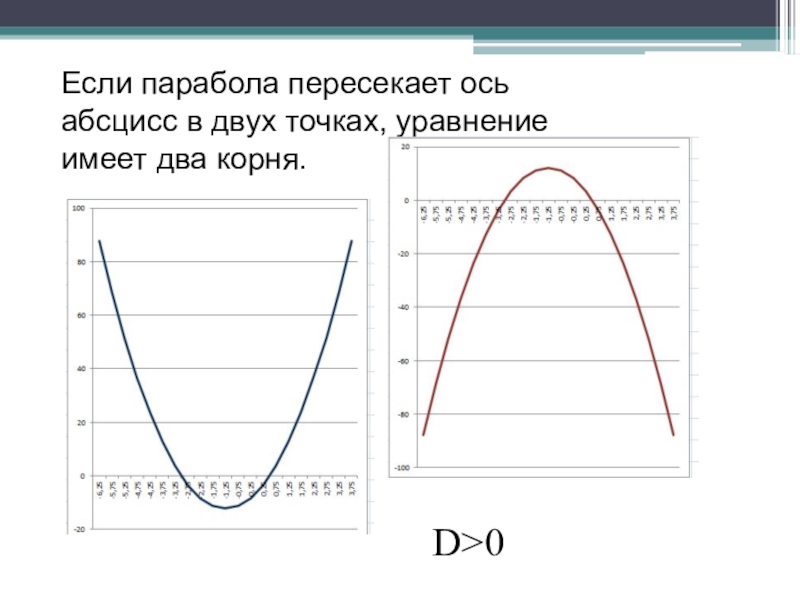
- 41. Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два корня.D>0
- 42. Домашнее заданиеНаписать программу на Excel для вычисления: процентов успеваемости и качества; среднего балла.
- 43. Спасибо за урок!
Цель урока: Обеспечить умение решить расчетные задачи с использованием математических функций для решения квадратного уравнения в среде электронных таблиц Excel, повторение относительных и абсолютных ссылок, отработка навыков построения графиков функций в среде электронных
Слайд 1Графический способ решения квадратных уравнений с помощью Excel
Интегрированный урок математики и
информатики
Слайд 2
Цель урока:
Обеспечить умение решить расчетные задачи
с использованием математических функций для решения квадратного уравнения в среде электронных таблиц Excel, повторение относительных и абсолютных ссылок, отработка навыков построения графиков функций в среде электронных таблиц Excel; повторение формул нахождения дискриминанта и корней квадратного уравнения.
Слайд 10Определить количество корней в уравнении:
Вариант I
9y2+6y+1=0;
2x2+8x+13=0.
Вариант II
4y2-4y+1=0;
3x2+32x+80=0;
Вариант III
x2+10x+25=0;
3x2+5x+15=0.
Слайд 11 «Недостойно одаренному человеку, тратить подобно рабу, часы на
вычисления, которые, безусловно, можно было бы доверить любому лицу, если при этом применить машину»
Готфрид Лейбниц (1646 – 1716) – немецкий
математик, физик, философ, юрист, языковед.
Готфрид Лейбниц (1646 – 1716) – немецкий
математик, физик, философ, юрист, языковед.
Слайд 12Электронные таблицы (ЭТ)
1) Для чего предназначены электронные таблицы?
(ЭТ – это
инструмент для табличных расчетов)
2) Из чего состоит имя ячейки?
(Из имени столбца и номера строки. Например, А1, В7, F12.)
3) Что может быть содержимым ячейки?
(Текст, числовое значение или формула.)
4) Каковы правила записи формул в ячейках?
(Ввод формулы начинается со знака =, вся формула пишется в строку.)
5) Как выглядят знаки арифметических операций в ЭТ?
(«+» сложение, «–» вычитание, «*» умножение, «^» возведение в степень, «/» – деление)
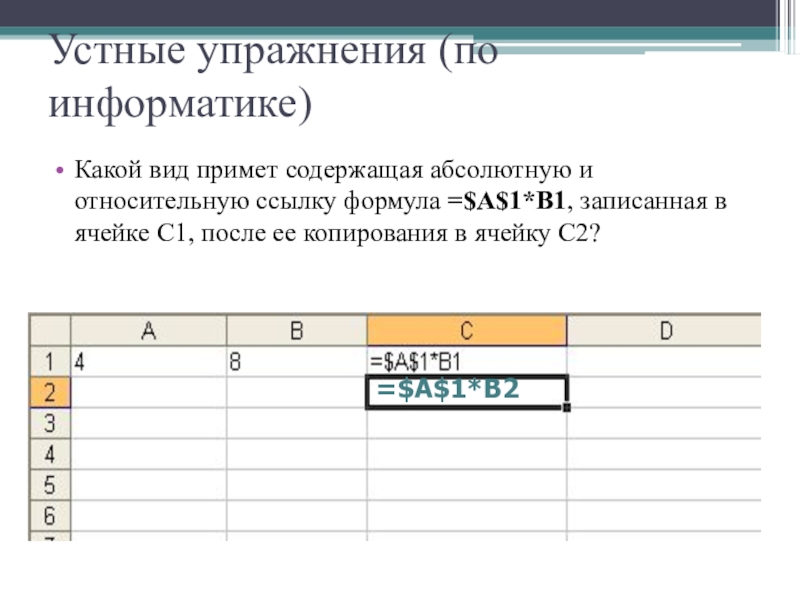
Слайд 13Устные упражнения (по информатике)
Какой вид примет содержащая абсолютную и относительную ссылку
формула =$A$1*B1, записанная в ячейке С1, после ее копирования в ячейку С2?
=$А$1*B2
Слайд 143. Дан фрагмент электронной таблицы:
В ячейку D2 введена формула =А2*В1+С1. В
результате в ячейке D2 появится значение:
1) 6 2) 14 3) 16 4) 24
1) 6 2) 14 3) 16 4) 24
24
Слайд 154. Дан фрагмент электронной таблицы:
В ячейку D1 введена формула =$А$1*В1+С2, а
затем скопирована в ячейку D2. Какое значение в результате появится в ячейке D2?
1) 10 2) 14 3) 16 4) 24
1) 10 2) 14 3) 16 4) 24
14
Слайд 16Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью
абсцисс.
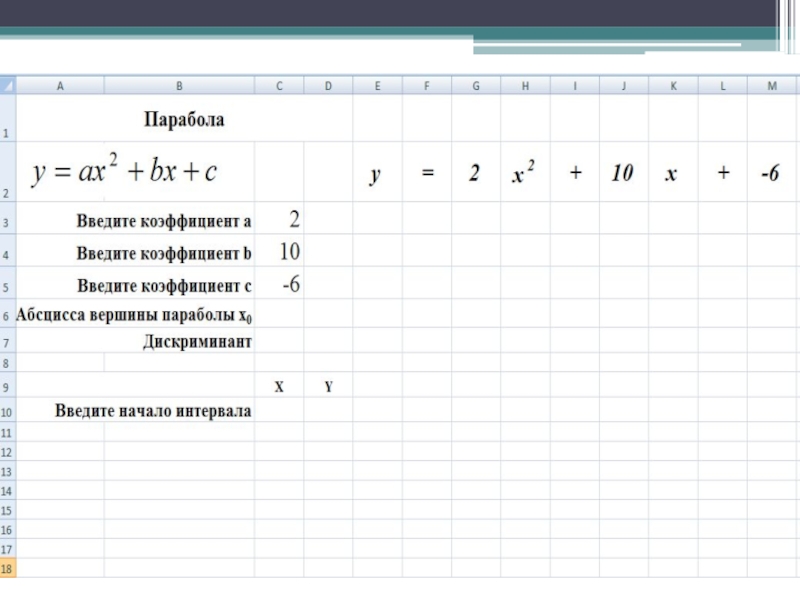
Слайд 17Решим квадратное уравнение
2x2+10x-6=0.
Для этого построим график функции y=2x2+10x-6
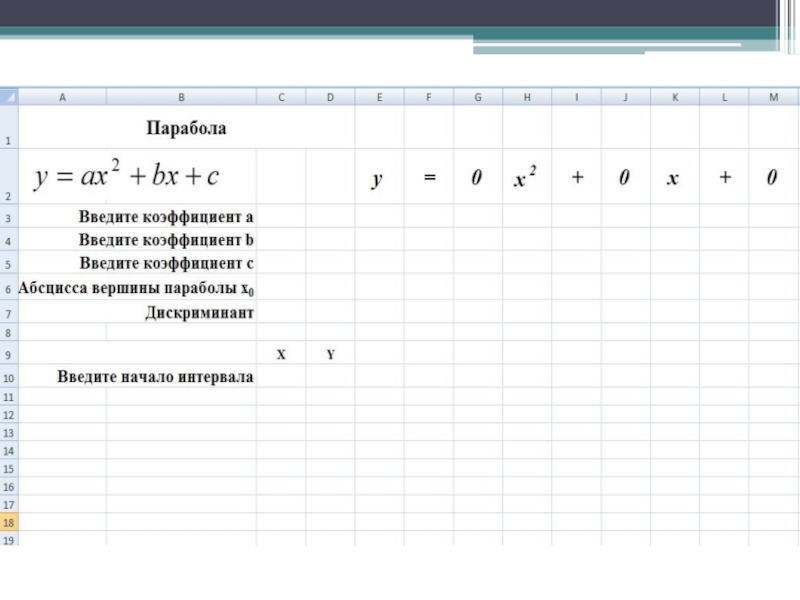
1. Откройте файл
Рабочий
стол/Заготовка
2. Введите коэффициенты a, b, c.
2. Введите коэффициенты a, b, c.
Слайд 35Физминутка
«Здоровье - не все, но все без здоровья - ничто». Сократ
«Здоровье - не все, но все без здоровья - ничто». Сократ
«Здоровье - не все, но все без здоровья - ничто». Сократ
«Здоровье - не все, но все без здоровья - ничто». Сократ
«Здоровье - не все, но все без здоровья - ничто». Сократ
«Здоровье - не все, но все без здоровья - ничто». Сократ
«Здоровье - не все, но все без здоровья - ничто».
Сократ
Простейшие упражнения для глаз:
вертикальные движения глаз вверх – вниз;
горизонтальное вправо – влево;
вращение глазами по часовой стрелке и против;
закрыть глаза и представить по очереди цвета радуги как можно отчетливее;
глазами «нарисовать» эти фигуры несколько раз в одном, а затем в другом направлении.
Слайд 39 Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс,
уравнение не имеет корней.
D<0
Слайд 40Если парабола пересекается с осью абсцисс в одной точке (в вершине
параболы), уравнение имеет один корень (также говорят, что уравнение имеет два совпадающих корня).
D=0
Слайд 42Домашнее задание
Написать программу на Excel для вычисления:
процентов успеваемости и
качества;
среднего балла.
среднего балла.
