- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Формула Шеннона
Содержание
Слайд 2
ФОРМУЛА ШЕННОНА
Количество информации для событий с различными вероятностями определяется по формуле:
Если
I – количество информации,
N – количество возможных событий
pi – вероятности отдельных событий
Слайд 3
ЗАДАНИЕ «БРОСАНИЕ ПЕРАМИДКИ»
Определить количество информации, которую мы получим в результате бросания
При бросании несимметричной четырехгранной пирамидки вероятности отдельных событий равны:
Количество информации рассчитываем по формуле:
p1=1/2; p2=1/4; p3=1/8; p4=1/8.
I = − (1/2·log21/2 + 1/4·log21/4 + 1/8·log21/8 + 1/8·log21/8) битов =
= (1/2·log22 + 1/4·log24 + 1/8·log28 + 1/8·log28) битов =
= (1/2 + 2/4+ 3/8+ 3/8) битов = 14/8 битов = 1,75 бита.
При бросании симметричной четырехгранной пирамидки вероятности отдельных событий равны между собой:
Количество информации рассчитываем по формуле:
p1= p2= p3= p4=1/4.
I = − log24 = 2 бита.
Количество информации, которую мы получаем, достигает
максимального значения, если события равновероятны.
Слайд 4
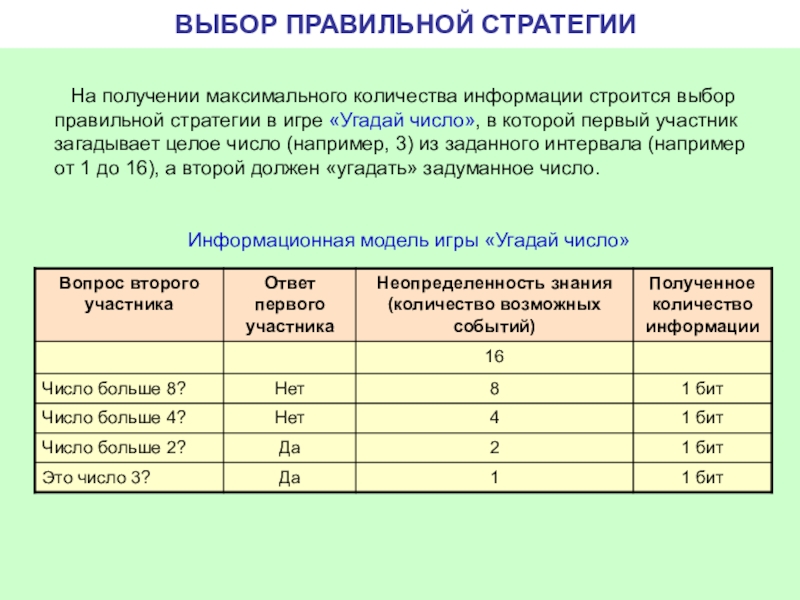
ВЫБОР ПРАВИЛЬНОЙ СТРАТЕГИИ
На получении максимального количества информации строится выбор
Информационная модель игры «Угадай число»
Слайд 5
КОМПЬЮТЕРНЫЙ ПРАКТИКУМ
Задача. В непрозрачном мешочке хранятся 10 белых, 30 красных, 30
Так как количество шариков различных цветов неодинаково, то вероятности зрительных сообщений о цвете вынутого из мешочка шарика также различаются и равны количеству шариков данного цвета, деленному на общее количество шариков:
Определение количества информации
рб = 0.1; pк = 0,2; рс = 0,3; рз = 0,4.
События неравновероятны, поэтому воспользуемся формулой
I = − (0,1·log2 0,1 + 0,2·log2 0,2 + 0,3·log2 0,3 + 0,4·log2 0,4) битов.
Для вычисления этого выражения воспользуемся компьютерным калькулятором Wise Calculator.
Таким образом, I ≈ 1,85 бита.