- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Домашнее задание по теме Введение в теорию графов
Содержание
- 1. Домашнее задание по теме Введение в теорию графов
- 2. Домашнее заданиеЛицей ИГУ, liguirk.ru*«Введение в ТГ [ДЗ].doc»Подготовиться к СР
- 3. Задача №1. Эйлеров графШесть островов на реке
- 4. Задача №2. Способы представления графов1) Определите вес
- 5. Задача №3. Кратчайший путьМежду населенными пунктами A,
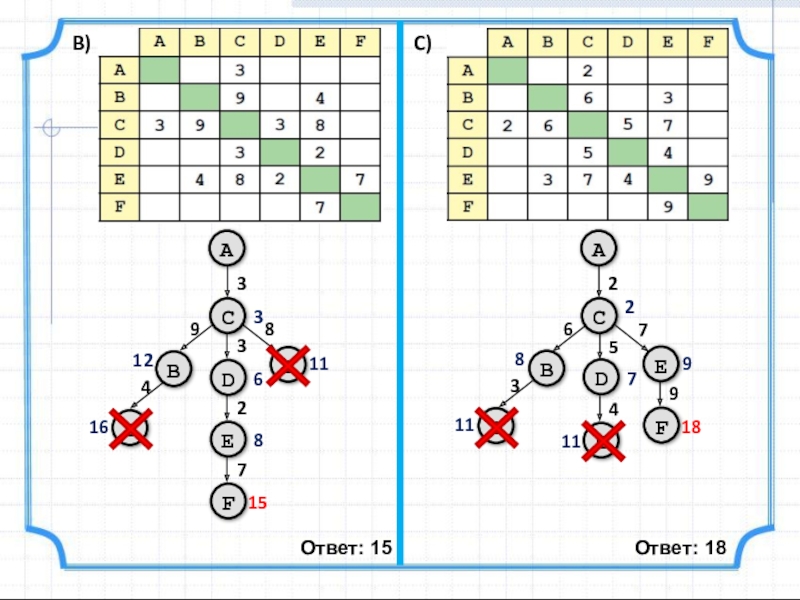
- 6. Ответ: 15Ответ: 18C)B)AA
- 7. Задача №4. Количество путейA) На рисунке показана
- 8. Задача №4. Количество путейB) На рисунке показана
- 9. Задача №4. Количество путейC) На рисунке –
- 10. Задача №5. Динамическое программированиеA) У исполнителя Калькулятор
- 11. Задача №5. Динамическое программированиеB) У исполнителя Калькулятор
- 12. Задача №5. Динамическое программированиеC) У исполнителя Калькулятор
- 13. Задача №5. Динамическое программированиеD) У исполнителя Калькулятор
Слайд 1Лицей ИГУ, liguirk.ru
Лавлинский М.В., LavlinskiMV@mail.ru
«Читайте, читайте Эйлера, он — наш общий
П.-С. Лаплас (1749 - 1827)
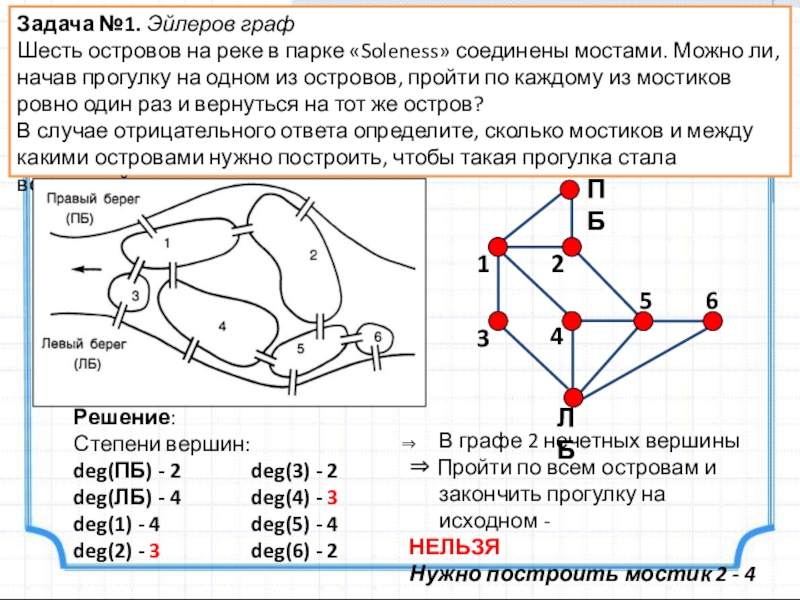
Слайд 3Задача №1. Эйлеров граф
Шесть островов на реке в парке «Soleness» соединены
В случае отрицательного ответа определите, сколько мостиков и между какими островами нужно построить, чтобы такая прогулка стала возможной.
Решение:
Степени вершин:
deg(ПБ) - 2
deg(ЛБ) - 4
deg(1) - 4
deg(2) - 3
deg(3) - 2
deg(4) - 3
deg(5) - 4
deg(6) - 2
В графе 2 нечетных вершины
⇒ Пройти по всем островам и закончить прогулку на исходном -
НЕЛЬЗЯ
Нужно построить мостик 2 - 4
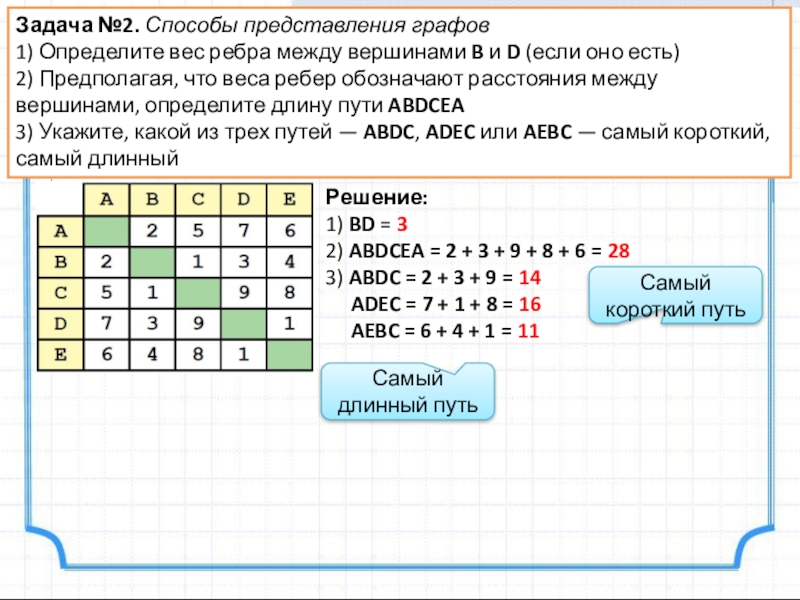
Слайд 4Задача №2. Способы представления графов
1) Определите вес ребра между вершинами B
2) Предполагая, что веса ребер обозначают расстояния между вершинами, определите длину пути ABDCEA
3) Укажите, какой из трех путей — ABDC, ADEC или AEBC — самый короткий, самый длинный
Решение:
1) BD = 3
2) ABDCEA = 2 + 3 + 9 + 8 + 6 = 28
3) ABDC = 2 + 3 + 9 = 14
ADEC = 7 + 1 + 8 = 16
AEBC = 6 + 4 + 1 = 11
Самый короткий путь
Самый длинный путь
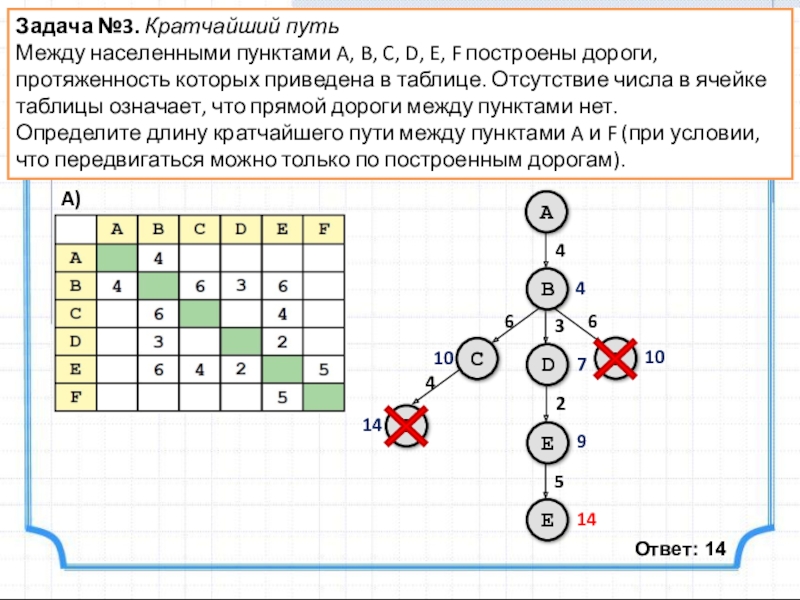
Слайд 5Задача №3. Кратчайший путь
Между населенными пунктами A, B, C, D, E,
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
A)
Ответ: 14
A
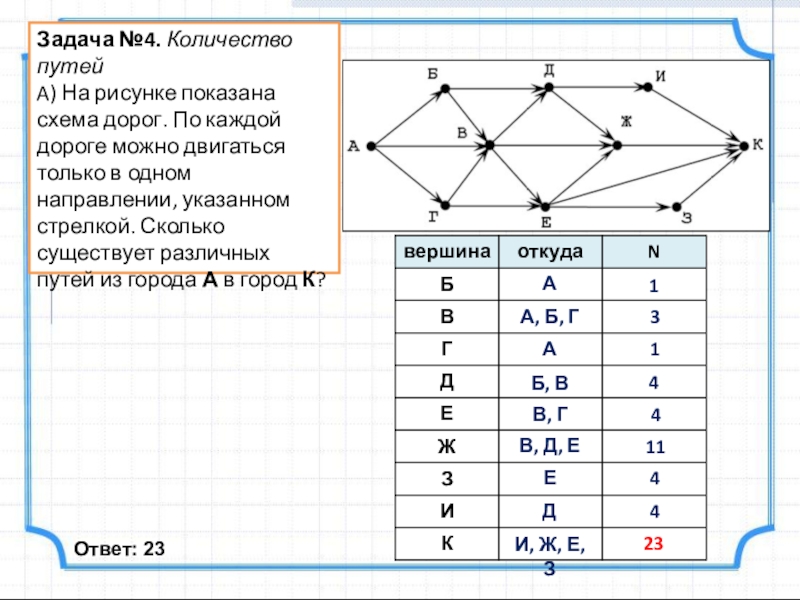
Слайд 7Задача №4. Количество путей
A) На рисунке показана схема дорог. По каждой
Ответ: 23
А
1
А, Б, Г
А
Б, В
В, Г
В, Д, Е
Е
Д
И, Ж, Е, З
1
3
4
4
11
4
4
23
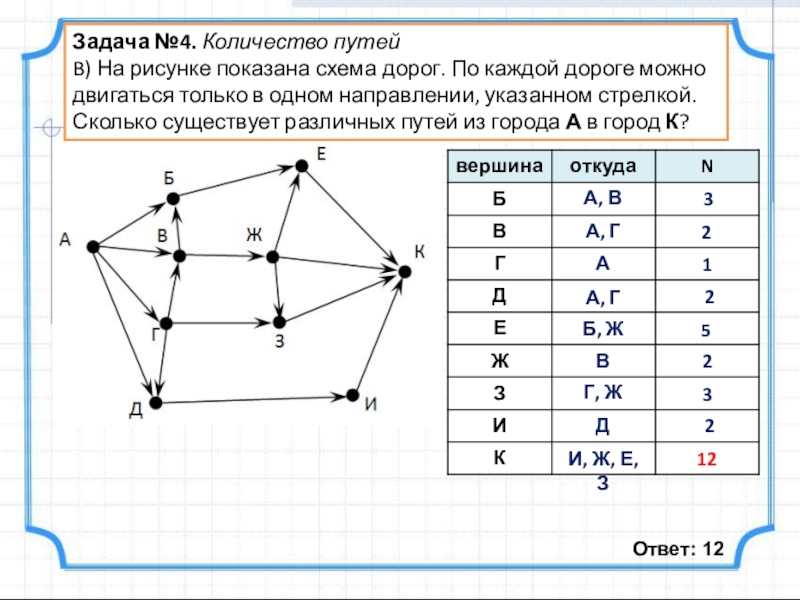
Слайд 8Задача №4. Количество путей
B) На рисунке показана схема дорог. По каждой
Ответ: 12
А, В
1
А, Г
А
А, Г
Б, Ж
В
Г, Ж
Д
И, Ж, Е, З
3
12
2
2
2
5
3
2
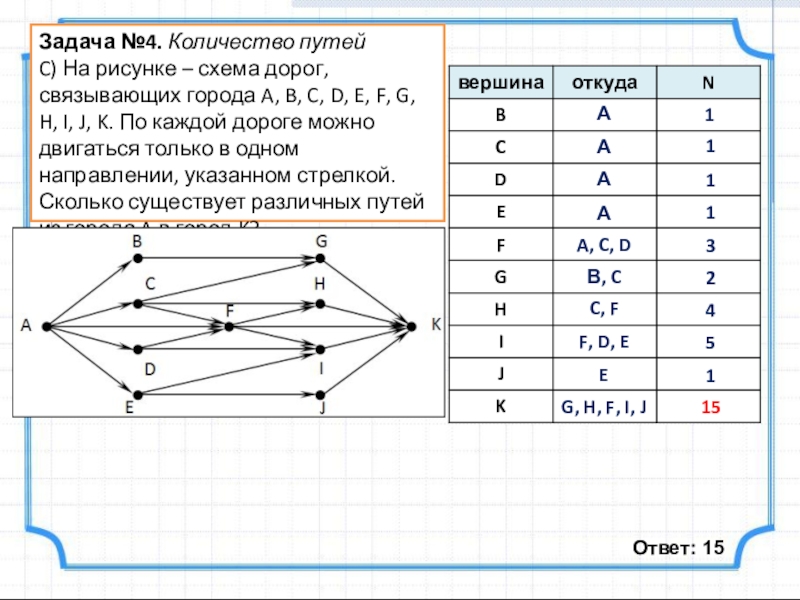
Слайд 9Задача №4. Количество путей
C) На рисунке – схема дорог, связывающих города
Ответ: 15
А
1
А
А
А
A, C, D
В, C
C, F
F, D, E
E
3
15
2
5
G, H, F, I, J
1
1
1
4
1
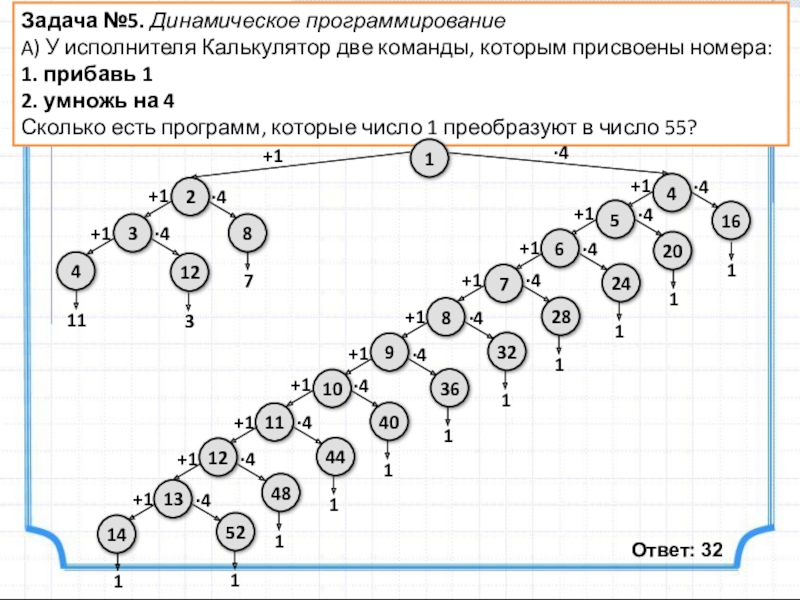
Слайд 10Задача №5. Динамическое программирование
A) У исполнителя Калькулятор две команды, которым присвоены
1. прибавь 1
2. умножь на 4
Сколько есть программ, которые число 1 преобразуют в число 55?
Ответ: 32
1
8
16
20
24
4
5
6
32
8
7
28
9
36
44
11
10
40
12
48
13
14
52
2
3
4
12
Слайд 11Задача №5. Динамическое программирование
B) У исполнителя Калькулятор три команды, которым присвоены
1. прибавь 1
2. умножь на 2
3. умножь на 3
Сколько есть программ, которые число 1 преобразуют в число 18?
Ответ: 96
2
1
3
2
4
6
3
6
9
18
10
18
12
6
7
4
12
8
16
9
5
15
10
8
14
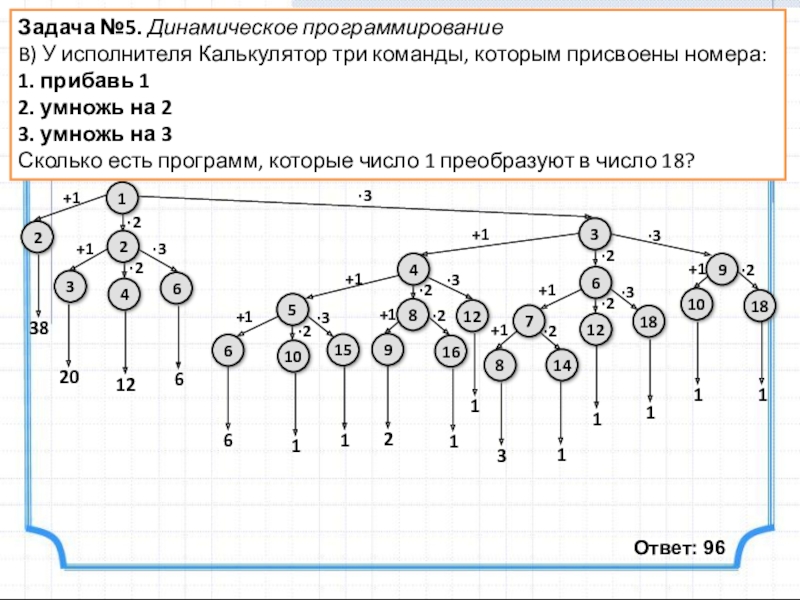
Слайд 12Задача №5. Динамическое программирование
C) У исполнителя Калькулятор три команды, которым присвоены
1. прибавь 1
2. умножь на 2
3. возведи в квадрат
Сколько есть программ, которые число 2 преобразуют в число 38?
Ответ: 266
2
4
4
6
9
4
6
25
10
20
16
5
8
32
17
34
9
18
11
22
8
7
12
3
36
36
20
38
24
13
26
16
14
28
12
15
14
10
19
18
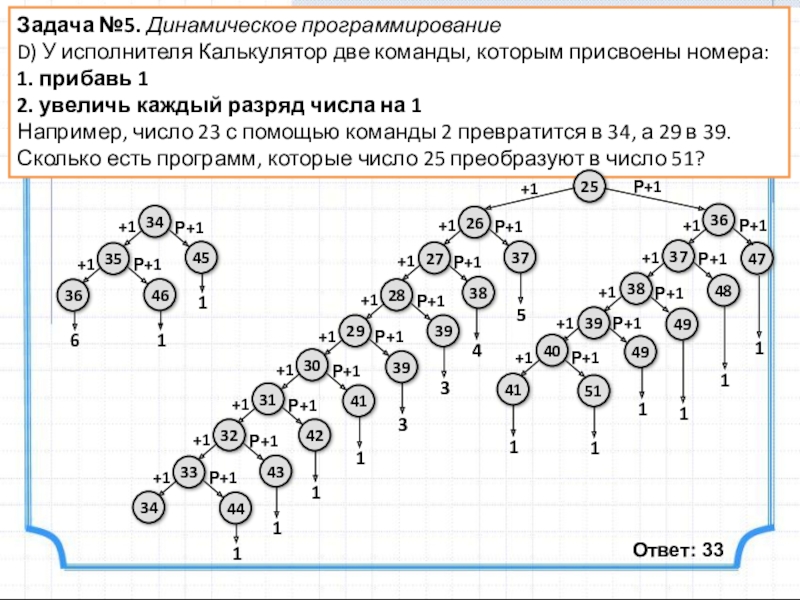
Слайд 13Задача №5. Динамическое программирование
D) У исполнителя Калькулятор две команды, которым присвоены
1. прибавь 1
2. увеличь каждый разряд числа на 1
Например, число 23 с помощью команды 2 превратится в 34, а 29 в 39.
Сколько есть программ, которые число 25 преобразуют в число 51?
Ответ: 33
25
48
39
47
49
49
40
51
41
37
36
37
38
38
39
26
27
28
39
29
41
30
42
31
43
32
44
33
45
34
34
46
35
36

![Домашнее задание по теме Введение в теорию графов Домашнее заданиеЛицей ИГУ, liguirk.ru*«Введение в ТГ [ДЗ].doc»Подготовиться к СР Домашнее заданиеЛицей ИГУ, liguirk.ru*«Введение в ТГ [ДЗ].doc»Подготовиться к СР](/img/thumbs/acf3e71ade6f0f2ed8a0bca2fa510506-800x.jpg)