категории
МБОУ «Лицей «Дубна»
Жевтило Ирина Аскольдовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Анализ программ с подпрограммами, содержащими модуль
Содержание
- 1. Анализ программ с подпрограммами, содержащими модуль
- 2. 21_1Определите, какое число будет напечатано в результате
- 3. запишем заданную функцию в привычном «математическом» виде:f(x)
- 4. 1) рассматриваем интервал (–; –5), раскрываем модули
- 5. 4) Найдем точки пересечения с ОХg(x) =
- 6. 21_2Определите, какое число будет напечатано в результате
- 7. запишем заданную функцию в привычном «математическом» виде:f(x)
- 8. 1) рассматриваем интервал (–; –5), раскрываем модули
- 9. 4) на всей числовой оси функция g(x)
21_1Определите, какое число будет напечатано в результате выполнения следующего алгоритма: Var a,b,t,M,R:integer;Function F(x:integer):integer;begin F:= abs( abs(x-5) + abs(x+5)- 20 ) + 4;end;BEGIN a:=-20; b:=20; M:=a; R:=F(a); for t:=a to b do begin if (F(t)
Слайд 1ЕГЭ21
Анализ программ с подпрограммами, содержащими модуль модулем
Учитель информатики и ИКТ высшей
Слайд 221_1
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var
a,b,t,M,R:integer;
Function F(x:integer):integer;
begin
F:= abs( abs(x-5) + abs(x+5)- 20 ) + 4;
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t) M:=t;
R:=F(t);
end;
end;
write(M+R);
END.
Function F(x:integer):integer;
begin
F:= abs( abs(x-5) + abs(x+5)- 20 ) + 4;
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)
R:=F(t);
end;
end;
write(M+R);
END.
g=43
n*n*n < 43
i=3, входит в цикл и печатает 4
Слайд 3запишем заданную функцию в привычном «математическом» виде:
f(x) = | | x
– 5 | + | x + 5 | – 20 | + 4
чтобы найти минимум этой функции, нужно представлять, как идёт её график
сначала рассмотрим функцию под знаком «большого» модуля g(x) = | x – 5 | + | x + 5 | – 20;
находим нули выражений под знаком модуля и отмечаем их на числовой оси:
чтобы найти минимум этой функции, нужно представлять, как идёт её график
сначала рассмотрим функцию под знаком «большого» модуля g(x) = | x – 5 | + | x + 5 | – 20;
находим нули выражений под знаком модуля и отмечаем их на числовой оси:
Слайд 41) рассматриваем интервал (–; –5), раскрываем модули (оба с обратным знаком):
g(x)
= – (x – 5) – (x + 5) – 20 = –2x – 20
на этом интервале функция g(x) убывает
2) рассматриваем полуинтервал [–5; 5), раскрываем модули:
g(x) = – (x – 5) + (x + 5) – 20 = – 10
на этом интервале значение функции g(x) постоянно
3) рассматриваем полуинтервал [5; ), раскрываем модули:
g(x) = (x – 5) + (x + 5) – 20 = 2x – 20
на этом интервале функция g(x) возрастает
график функции g(x) показан на рисунке
на этом интервале функция g(x) убывает
2) рассматриваем полуинтервал [–5; 5), раскрываем модули:
g(x) = – (x – 5) + (x + 5) – 20 = – 10
на этом интервале значение функции g(x) постоянно
3) рассматриваем полуинтервал [5; ), раскрываем модули:
g(x) = (x – 5) + (x + 5) – 20 = 2x – 20
на этом интервале функция g(x) возрастает
график функции g(x) показан на рисунке
Слайд 54) Найдем точки пересечения с ОХ
g(x) = –2x – 20 =
0 x = – 10
g(x) = 2x – 20 = 0 x = 10
5) т.к. f(x) = | g(x) | + 4, за счёт модуля отрицательные значения изменятся на положительные и к ним добавится 4.
6) функция f(x) будет иметь минимальные значения, равные 4, как раз в точках x = – 10 и x = 10
7) Т.к. неравенство строгое, то запомнит первую точку x = – 10
8) Выводит на печать M+R, поэтому результат будет равен
(–10) + 4 = – 6
Ответ: – 6.
g(x) = 2x – 20 = 0 x = 10
5) т.к. f(x) = | g(x) | + 4, за счёт модуля отрицательные значения изменятся на положительные и к ним добавится 4.
6) функция f(x) будет иметь минимальные значения, равные 4, как раз в точках x = – 10 и x = 10
7) Т.к. неравенство строгое, то запомнит первую точку x = – 10
8) Выводит на печать M+R, поэтому результат будет равен
(–10) + 4 = – 6
Ответ: – 6.
Слайд 621_2
Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var
a,b,t,M,R:integer;
Function F(x:integer):integer;
begin
F:= abs( abs(x-5) + abs(x+5) - 3) + 12;
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t) M:=t;
R:=F(t);
end;
end;
write(M+R);
END.
Function F(x:integer):integer;
begin
F:= abs( abs(x-5) + abs(x+5) - 3) + 12;
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)
R:=F(t);
end;
end;
write(M+R);
END.
Слайд 7запишем заданную функцию в привычном «математическом» виде:
f(x) = | | x
– 5 | + | x + 5 | – 3 | + 12
чтобы найти минимум этой функции, нужно представлять, как идёт её график
сначала рассмотрим функцию под знаком «большого» модуля g(x) = | x – 5 | + | x + 5 | – 3;
находим нули выражений под знаком модуля и отмечаем их на числовой оси:
чтобы найти минимум этой функции, нужно представлять, как идёт её график
сначала рассмотрим функцию под знаком «большого» модуля g(x) = | x – 5 | + | x + 5 | – 3;
находим нули выражений под знаком модуля и отмечаем их на числовой оси:
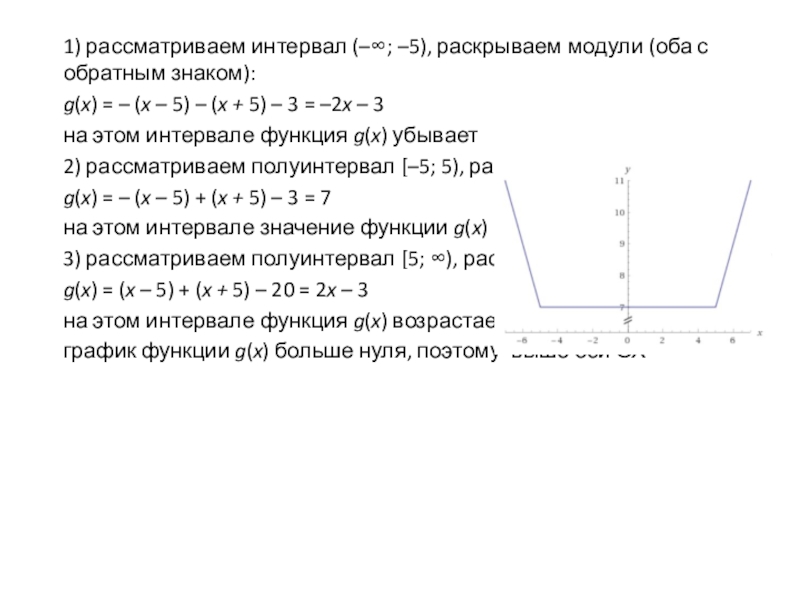
Слайд 81) рассматриваем интервал (–; –5), раскрываем модули (оба с обратным знаком):
g(x)
= – (x – 5) – (x + 5) – 3 = –2x – 3
на этом интервале функция g(x) убывает
2) рассматриваем полуинтервал [–5; 5), раскрываем модули:
g(x) = – (x – 5) + (x + 5) – 3 = 7
на этом интервале значение функции g(x) постоянно
3) рассматриваем полуинтервал [5; ), раскрываем модули:
g(x) = (x – 5) + (x + 5) – 20 = 2x – 3
на этом интервале функция g(x) возрастает
график функции g(x) больше нуля, поэтому выше оси ОХ
на этом интервале функция g(x) убывает
2) рассматриваем полуинтервал [–5; 5), раскрываем модули:
g(x) = – (x – 5) + (x + 5) – 3 = 7
на этом интервале значение функции g(x) постоянно
3) рассматриваем полуинтервал [5; ), раскрываем модули:
g(x) = (x – 5) + (x + 5) – 20 = 2x – 3
на этом интервале функция g(x) возрастает
график функции g(x) больше нуля, поэтому выше оси ОХ
Слайд 94) на всей числовой оси функция g(x) принимает положительные значения, так
что | g(x) | = g(x), поэтому
f(x) = | g(x) | + 12 = g(x) + 12
во всех точках на отрезке [-5; 5] функции f(x) равно 7 + 12 = 19, поэтому программа найдёт одну из этих точек как точку минимума
5) функция f(x) будет иметь минимальные значения, равные 19, как раз в интервале от -5 до 5
7) Т.к. неравенство строгое, то запомнит первую точку x = – 5
8) Выводит на печать M+R, поэтому результат будет равен
(–5) + 19 = 14
Ответ: 14.
f(x) = | g(x) | + 12 = g(x) + 12
во всех точках на отрезке [-5; 5] функции f(x) равно 7 + 12 = 19, поэтому программа найдёт одну из этих точек как точку минимума
5) функция f(x) будет иметь минимальные значения, равные 19, как раз в интервале от -5 до 5
7) Т.к. неравенство строгое, то запомнит первую точку x = – 5
8) Выводит на печать M+R, поэтому результат будет равен
(–5) + 19 = 14
Ответ: 14.