- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Аналитическое решение уравнений и их систем в пакетах символьной математики.
Содержание
- 1. Аналитическое решение уравнений и их систем в пакетах символьной математики.
- 2. MathematicaДля решения дифференциальных уравнений в аналитической форме
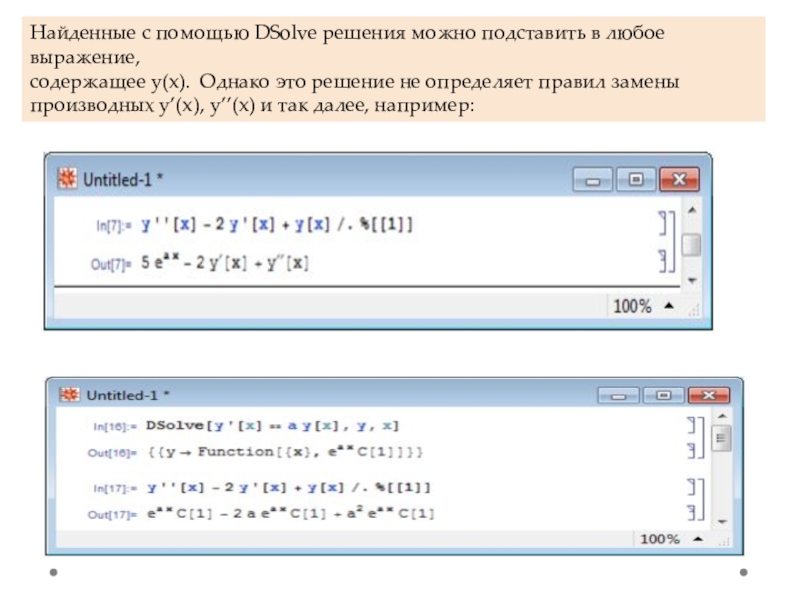
- 3. Найденные с помощью DSolve решения можно подставить
- 4. Для решения систем уравнений в качестве первого
- 5. Для некоторых уравнений решение может быть выражено
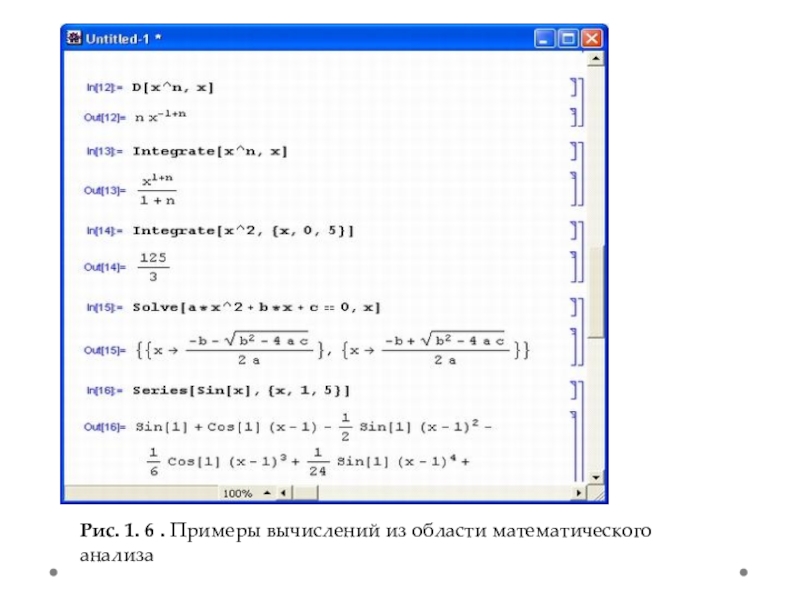
- 6. Примеры из математического
- 7. Рис. 1. 6 . Примеры вычислений из области математического анализа
- 8. В этих примерах функция D (как приятное
- 9. Системы символьной математики являются справочниками по многим
- 10. Здесь специальные функции получаются в результате вычисления
- 11. Приведем примеры решения дифференциальных уравнений:DSolve [Derivative [1]
- 12. MapleАналитическое решение дифференциальных уравненийОбщее решение дифференциальных уравнений.Для
- 13. Общее решение дифференциального уравнения зависит от произвольных
- 14. Общее решение неоднородного линейного дифференциального уравнения всегда
- 15. Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате.
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. MathcadАналитические вычисления в MathcadС помощью аналитических вычислений
- 20. Рис. 1.16
- 21. Слайд 21
- 22. Команды для выполнения аналитических вычислений в основном
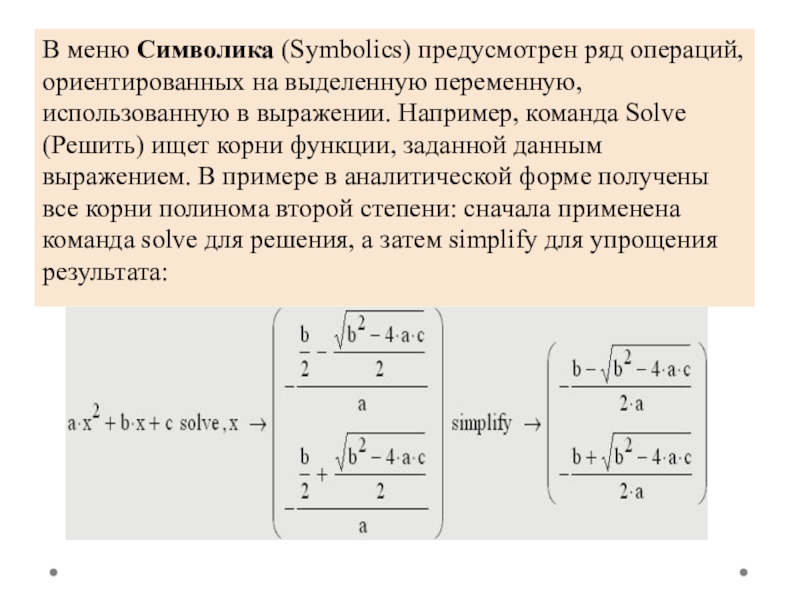
- 23. В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на
- 24. Другие возможности использования этого меню включают:аналитическое дифференцирование
- 25. замена переменной: Символика > Переменная > Подставить (Symbolics >
- 26. Механизм аналитических вычислений можно использовать для аналитического
- 27. Отметим, что функция Find пытается найти решение в аналитической
- 28. MATLABРешение систем дифференциальных уравнений в символьном виде
- 29. Пример решения задачиОбратите внимание, что уравнение, которое
- 30. Ответ представляет собой точное (символьное) решение (3
- 31. Например:
- 32. Спасибо за внимание!
Слайд 1Реферат
на тему:
Аналитическое решение уравнений и их систем в пакетах символьной математики
Студентка:
Слайд 2Mathematica
Для решения дифференциальных уравнений в аналитической
форме в пакете Mathematica используется
Для получения частного решения необходимо в качестве первого аргумента
DSolve указать список, состоящий из самого уравнения и начальных
или граничных условий:
Слайд 3Найденные с помощью DSolve решения можно подставить в любое выражение,
содержащее
производных y’(x), y’’(x) и так далее, например:
Слайд 4Для решения систем уравнений в качестве первого аргумента
функции указывается список
аргумента – список искомых функций:
Если в список уравнений включить необходимое количество
начальных или граничных условий, то будет найдено частное
решение системы ДУ, не содержащее произвольных постоянных:
Слайд 5Для некоторых уравнений решение может быть выражено через
спецфункции, встроенные в
Если же DSolve не может найти аналитического решения ДУ,
то Mathematica просто перепечатывает введенные данные в выходную ячейку:
В этом случае нужно преобразовать ДУ к более простому виду,
используя правила, известные из теории дифференциальных уравнений.
Если же аналитически решить уравнение не удается,
можно попробовать решить его численно.
Слайд 6
Примеры из математического анализа
Разумеется, роль систем символьной математики далеко не исчерпывается
Слайд 8В этих примерах функция D (как приятное исключение из правил, обозначенная
Слайд 9Системы символьной математики являются справочниками по многим специальным функциям. При этом
Слайд 10Здесь специальные функции получаются в результате вычисления суммы, символьного интегрирования и
Слайд 11Приведем примеры решения дифференциальных уравнений:
DSolve [Derivative [1] [у] [х] ==2*а*х^3, у[х],
{{у[х]->aх4/2+С[1]}}
DSolve[{yl' [х] == 2 х2, у2' [х] == 3 х}, {yl[х], у2[х]}, х]
{{yl[x] ->-2х3/3+C[1], у2[х] ->3х2/2+C[2]}}
DSo2ve{y'[x] +у[х] ==х, у[х], х}
{{у[х] -*-1+х + е-хС[1]}}
DSolve [у" [х] - у' [х] - 6 у [х] == 0, у [х] , х] {{У[х] ->| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]}}
DSolve [у" [х] + 4 у'[х] == 10 Sin [2 х] , у [х] , х]
{{У[х] ->| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]}}
DSolve[y'[x] == Sin[Ex] , y[x] , x]
{{y[x] ->C[1] +Sinlntegral[ex]}}
DSolvefz2 w"[z] +zw'[z] - (z2 + l)w[z] ==0, w[z], z]
{{w[z] ->BesselI[l, z] C[l] +BesselK[l, z] C[2] }}
Слайд 12Maple
Аналитическое решение дифференциальных уравнений
Общее решение дифференциальных уравнений.
Для нахождения аналитических решений дифференциальных
Слайд 13Общее решение дифференциального уравнения зависит от произвольных постоянных, число которых равно
Слайд 14Общее решение неоднородного линейного дифференциального уравнения всегда выводится так, чтобы была
Слайд 15Команда dsolve выдает решение дифференциального уравнения в невычисляемом формате. Для того, чтобы с
Слайд 19Mathcad
Аналитические вычисления в Mathcad
С помощью аналитических вычислений находят аналитические или полные
Слайд 22Команды для выполнения аналитических вычислений в основном сосредоточены в меню Символика (Symbolics) и
Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Символика > Упростить (Symbolics > Simplify). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции. Некоторые действия по раскрытию скобок и упрощению сложных тригонометрических выражений требуют применения команды Символика > Раскрыть/Расширить (Symbolics > Expand).
Слайд 23В меню Символика (Symbolics) предусмотрен ряд операций, ориентированных на выделенную переменную, использованную в
Слайд 24Другие возможности использования этого меню включают:
аналитическое дифференцирование и интегрирование: Символика > Переменная
Слайд 25замена переменной: Символика > Переменная > Подставить (Symbolics > Variable > Substitute) –
Слайд 26Механизм аналитических вычислений можно использовать для аналитического решения уравнений и систем
Find(х,у,...) ,
где в скобках приведен список искомых величин, а далее следует знак аналитического вычисления, отображаемый в виде стрелки, направленной вправо:
Слайд 27Отметим, что функция Find пытается найти решение в аналитической форме. В том случае,
Примеры использования функции Find для решения уравнений и систем уравнений различного типа приведены в соответствующих разделах пособия.
Любое аналитическое вычисление можно применить с помощью ключевого слова. Cписок ключевых слов
Слайд 28MATLAB
Решение систем дифференциальных уравнений в символьном виде в системе MATLAB
Для решения
По умолчанию независимой переменной считается ‘t’ . Можно использовать и другую переменную, включив ее в конец списка параметров функции dsolve. Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d^2/dt^2 и т.д.
Начальные условия задаются в виде равенств ‘y(a) = b’ или ‘Dy(a) = b’, где y - независимая переменная, a и b – константы. Если число начальных условий меньше, чем число дифференциальных уравнений, то в решений будут присутствовать произвольные постоянные С1, С2 и т.д. Вывод осуществляется в виде массива записей.








![Аналитическое решение уравнений и их систем в пакетах символьной математики. Приведем примеры решения дифференциальных уравнений:DSolve [Derivative [1] [у] [х] ==2*а*х^3, у[х], Приведем примеры решения дифференциальных уравнений:DSolve [Derivative [1] [у] [х] ==2*а*х^3, у[х], х]{{у[х]->aх4/2+С[1]}}DSolve[{yl' [х] == 2 х2, у2'](/img/thumbs/325fdc101828dbb90f1c56f36ee08fec-800x.jpg)