- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по аналитической химии Электролитическая диссоциация
Содержание
- 1. Презентация по аналитической химии Электролитическая диссоциация
- 2. неэлектролитывеществаэлектролиты не проводят эл. ток частицы раств.
- 3. Количественно ионизация электролита в растворе характеризуется степенью
- 4. Слабые и сильные электролитыслабые
- 5. Частицы в растворах взаимодействуют друг с другом.
- 6. Термодинамические уравнения (в частности константа равновесия является
- 7. Чтобы использовать для реальных систем общие термодинамические
- 8. Активность ионов в растворе - это величина,
- 9. При с = 0 величина а =
- 10. Коэффициенты активности зависят от заряда иона и
- 11. Связь коэффициента активности с ионной силой описывается
- 12. Из этих уравнений следует, что если ионная
- 13. Рассмотрим электролит, молекулы которого XY распадаются в
- 14. Если электролит сильный (α = 1), концентрация
- 15. К физическому смыслу произведения αС можно прийти
- 16. Напомним, что в выражении для степени диссоциации
- 17. Итак, мы приходим к тому же выводу:
- 18. Концентрация недиссоциированных молекул [HCN] в равновесии должна
- 19. Это не что иное, как математическая формулировка
- 20. Полезность закона разбавления не исчерпывается определением констант
- 21. ЗАДАЧА. Сколько воды надо прибавить к 300
- 22. Подсказка к задаче . Эта задача проще,
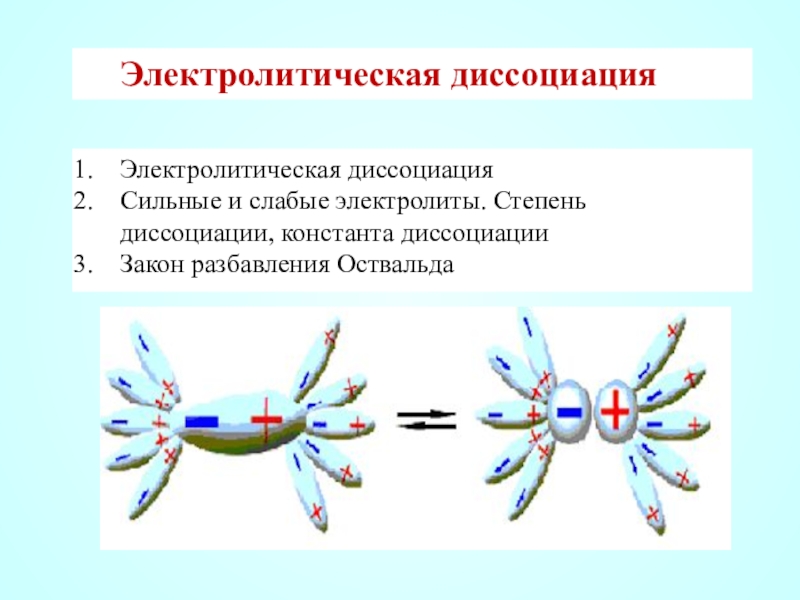
Слайд 1Электролитическая диссоциация
Электролитическая диссоциация
Сильные и слабые электролиты. Степень диссоциации, константа диссоциации
Закон
Слайд 2неэлектролиты
вещества
электролиты
не проводят эл. ток
частицы раств. в-ва =
=
оксиды, орг. вещества
проводят эл. Ток
частицы раств. в-ва =
= ИОНЫ + МОЛЕКУЛЫ
соли, кислоты, основания
Электролиты - вещества,
способные распадаться
на ионы в растворе
Слайд 3Количественно ионизация электролита в растворе
характеризуется степенью диссоциации (а), равной
отношению
к исходному числу молекул.
Степень диссоциации численно выражается
либо в долях единицы, либо в процентах.
По способности к диссоциации электролиты
разделяют на сильные и слабые
Степень диссоциации
Слайд 4Слабые и сильные электролиты
слабые средней
0 3 % 3 % 30 % 30 % 100 %
1. H2O
2. Кислоты
H2CO3, H2S,
HCN, HNO3
CH3COOH
3. Основания
NH4OH
4. Некоторые соли
1. Кислоты
H2SO4, HNO3, HCl,
HBr, HJ, HClO4
2. Основания
LiOH, NaOH …
Ca(OH)2, Sr(OH)2,
Ba(OH)2
3. Все соли
Слайд 5Частицы в растворах взаимодействуют друг с другом.
Если эти взаимодействия отсутствуют,
считаются идеальными. Строго говоря, идеальных
растворов не существует и представляют собой
теоретическую абстракцию. Однако если концентрация
раствора электролита стремится к нулю,
расстояния между частицами увеличиваются,
а энергия их взаимодействия - уменьшается.
Поэтому свойства бесконечно разбавленных растворов
приближаются по свойствам к идеальным.
Состояние сильных электролитов в растворе
Слайд 6Термодинамические уравнения (в частности константа
равновесия является термодинамической
характеристикой реакции) для
растворов, в которых фигурируют концентрации,
непригодны для описания свойств реальных
растворов, так как каждый реальный раствор
к тому же имеет свою собственную специфику.
Состояние сильных электролитов в растворе
Слайд 7Чтобы использовать для реальных систем
общие термодинамические уравнения,
американский физико -
в 1907 г метод активностей, согласно которому
в эти уравнения вместо концентраций вводят
некие числа так, чтобы результаты, полученные
после решения этих уравнений, совпадали
с экспериментальными данными.
Такие числа называют «активностью».
Состояние сильных электролитов в растворе
Слайд 8Активность ионов в растворе - это величина,
подстановка которой вместо общей
в термодинамические уравнения для идеальных
растворов, дает соответствующие опыту
значения рассчитываемых величин для
реальных растворов.
Активность а связана с общей концентрацией с
формальным соотношением: а = с · f,
где f - коэффициент активности.
Состояние сильных электролитов в растворе
Слайд 9При с = 0 величина а = с, так что f
т.е. для предельно разбавленных растворов
активность по числовой величине совпадает
с концентрацией, а коэффициент активности равен 1.
Чем больше коэффициент активности отличается от 1,
тем сильнее свойства реального раствора отличаются
от идеального.
Константа равновесия, выраженная через
активность, называется истинной
термодинамической константой равновесия.
Состояние сильных электролитов в растворе
Слайд 10Коэффициенты активности зависят от заряда иона
и ионной силы раствора, которая
произведений концентрации каждого иона
на квадрат его зарядового числа I = 0,5 ΣCiZi2,
где I - ионная сила раствора,
Ci - молярная концентрация всех ионов,
Zi - зарядовое число ионов.
Ионная сила раствора
Слайд 11Связь коэффициента активности с ионной силой
описывается следующим уравнением:
lgfi = -A
где fi - коэффициент активности i -го иона;
zi - заряд этого иона; I - ионная сила раствора;
А - коэффициент, зависящий от температуры и природы
растворителя. Для водных растворов при 250 С
величина А = 0,512, поэтому можем записать:
lgfi = — 0,512 A zi2√I.
Это уравнение соответствует первому приближению
Дебая-Хюккеля и справедливо для значений I,
не превышающих 0,01 моль/л.
Ионная сила раствора
Слайд 12Из этих уравнений следует, что если ионная сила
раствора постоянна, то
имеющих одинаковый по абсолютной величине заряд,
коэффициент активности один и тот же.
В этом заключается правило ионной силы Льюиса и
Рендалла. В аналитике часто пользуются активностями,
т.к. ионная сила оказывает влияние и на увеличение
силы кислот и оснований и на растворимость
малорастворимых электролитов.
Ионная сила раствора
Слайд 13Рассмотрим электролит, молекулы которого XY
распадаются в растворе на два иона
Фактически, степень диссоциации α представляет собой
долю распавшихся молекул.
Если общую концентрацию электролита (С)
умножить на эту долю, то получим
концентрацию любого из ионов.
Иными словами, αС = [X+] моль/л, и αC = [Y–] моль/л.
Закон разбавления Оствальда
Слайд 14Если электролит сильный (α = 1),
концентрация каждого из ионов просто
исходной концентрации электролита.
Например, в 1 литре 0,1М раствора NaCl
содержится 0,1 моль ионов Na+ и 0,1 моль ионов Cl–
Закон разбавления Оствальда
Слайд 15К физическому смыслу произведения αС
можно прийти и другим путем.
Допустим,
(синильной кислоты) с концентрацией С моль/л.
В растворе циановодород слабо диссоциирует на ионы:
HCN ↔ H+ + CN–
Закон разбавления Оствальда
Слайд 16Напомним, что в выражении для степени диссоциации α
величина n0 отражает
HCN, изначально попавших в раствор.
Иными словами, n0 = C моль/л. Напомним также,
что n1 – это число молекул (или молей) HCN,
распавшихся на ионы.
Следовательно, n1 = [H+] и n1 = [CN–]. В этом случае:
α =
Отсюда следует, что [H+] = Cα, [CN–] = Cα.
Закон разбавления Оствальда
Слайд 17Итак, мы приходим к тому же выводу:
чтобы получить концентрацию любого
в растворе, достаточно общую концентрацию
вещества С умножить на коэффициент
α – степень его диссоциации.
Если теперь записать выражение для константы
диссоциации HCN, то можно выразить Кд через Сα:
Кд =
Закон разбавления Оствальда
Слайд 18Концентрация недиссоциированных молекул [HCN]
в равновесии должна быть меньше
исходной концентрации
– отсюда выражение (С – Сα) в знаменателе дроби.
Если вынести концентрацию С за скобки
и сократить, то получим следующее выражение:
Кд =
Или, в другой записи: Кд =
Закон разбавления Оствальда
Слайд 19Это не что иное, как математическая формулировка
закона разбавления Оствальда.
Закон
электролитов, т.е. веществ, молекулы которых в
растворе распадаются на два иона – катион и анион.
Однако в случае слабых электролитов величина (1 – α)
очень мало отличается от единицы.
Действительно, если α = 0,01, то (1 – 0,01) = 0,99,
т.е. практически 1. Таким образом, для слабых
электролитов закон разбавления Оствальда
можно записать в более простом виде:
Кд = α2 ∙ С
Закон разбавления Оствальда
Слайд 20Полезность закона разбавления не исчерпывается
определением констант диссоциации.
Простой пример его
вычислим точно степень диссоциации в 0,1М
растворе уксусной кислоты, если ее константа
диссоциации Кд = 1,8·10–5, электролит слабый
(Кд много меньше 1), можно воспользоваться законом
Разбавления для слабых электролитов: К = α2С.
Отсюда: α =
Подставляя в эту формулу численные значения, получим:
α = = 1,34 · 10-2 или 1,34%
Закон разбавления Оствальда
Слайд 21ЗАДАЧА. Сколько воды надо прибавить
к 300 миллилитрам 0,2 М
раствора уксусной
(Кд = 1,8·10–5),
чтобы степень диссоциации кислоты
удвоилась?
Закрепление
Слайд 22Подсказка к задаче . Эта задача проще,
чем может показаться на
Численное значение константы диссоциации кислоты
при решении вам не потребуется.
В задаче оно приведено для того, чтобы было понятно,
что кислота слабая и к ее растворам применим
закон разбавления Оствальда в виде: Кд = α2С.
По условию задачи степени диссоциации
после разбавления и до разбавления соотносятся как α2 = 2α1.
Если выразить обе α через закон разбавления,
то при дальнейшем решении значения Кд сокращаются.
Есть способ решения, в котором значение концентрации
раствора 0,2 М тоже не обязательно использовать
(напомним, что большая буква «М» означает «моль/л»).
Попробуйте найти это решение.
Закрепление
















![Презентация по аналитической химии Электролитическая диссоциация Концентрация недиссоциированных молекул [HCN] в равновесии должна быть меньше исходной концентрации Концентрация недиссоциированных молекул [HCN] в равновесии должна быть меньше исходной концентрации С как раз на величину Сα](/img/thumbs/65b121b01c621d8a7bbe155d628c3966-800x.jpg)