- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок по теме Параллельные прямые
Содержание
- 1. Урок по теме Параллельные прямые
- 2. Цели:Систематизировать знания по теме : признаки параллельности
- 3. Расшифруйте анаграммы:ОслопктьсЯрмыепЕн сепересяюткаЛепаарльеынлУщексяаРенвунтниелоуг
- 4. Закончить предложение:Параллельными прямыми….Перпендикулярными называются прямыми,….Если прямые перпендикулярны
- 5. Ответы :Называются прямые, которые не пересекаются.При пересечении
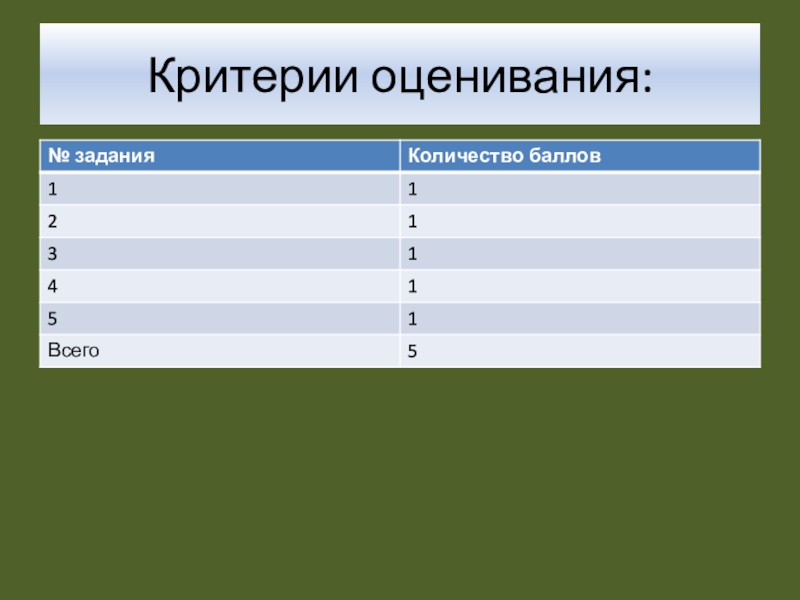
- 6. Критерии оценивания:
- 7. Слайд 7
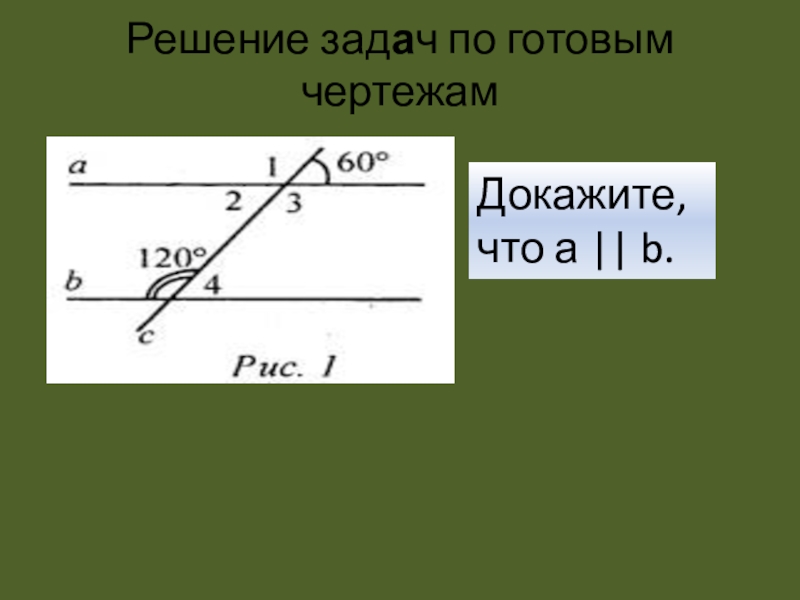
- 8. Решение задач по готовым чертежамДокажите, что а || b.
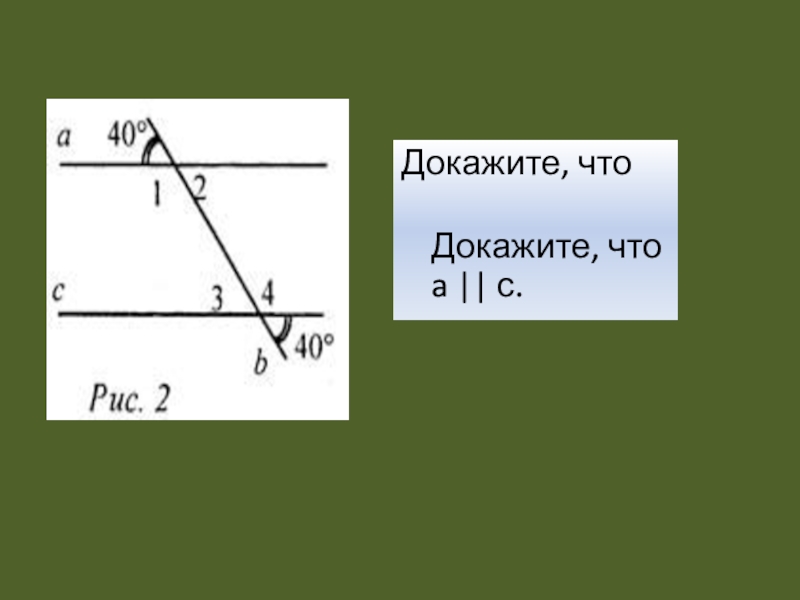
- 9. Докажите, что
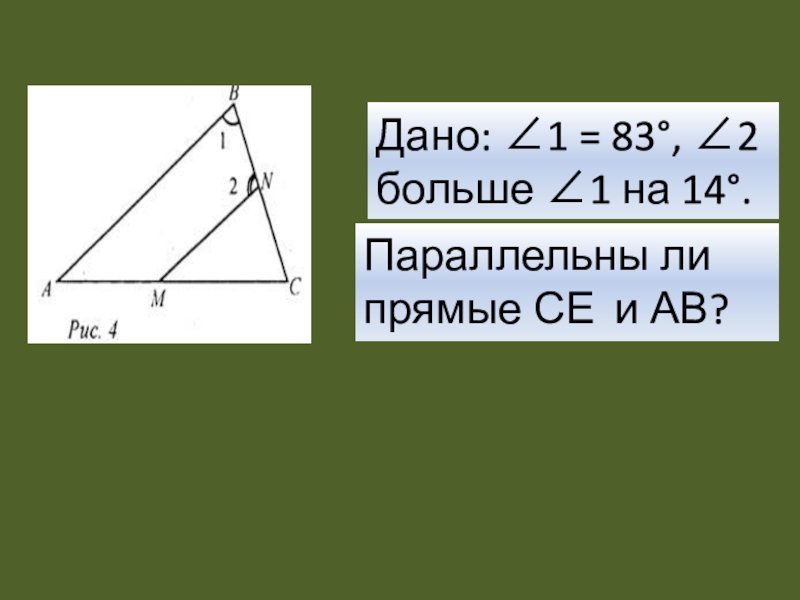
- 10. Дано: ∠1 = 83°, ∠2 больше ∠1 на 14°.Параллельны ли прямые СЕ и АВ?
- 11. Решить тест:Обведи кружочком правильный ответ.
- 12. 1)Вычеркнуть лишние слова в скобках:Аксиома – это
- 13. 5) Указать правильный ответ на вопрос.Если через
- 14. 6) Почему, если одна из прямых, проходящих
- 15. 7. Сколько углов образуется при пересечении двух
- 16. 11. При пересечении двух параллельных прямых третьей
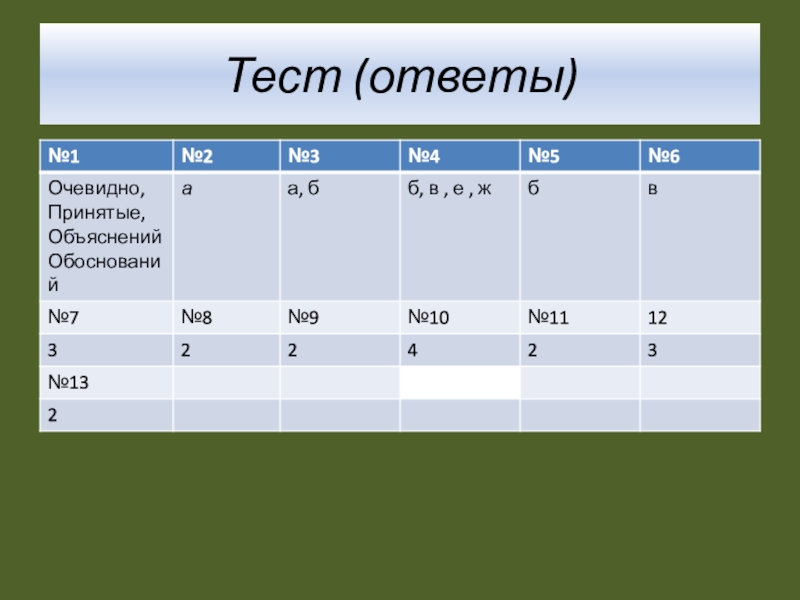
- 17. Тест (ответы)
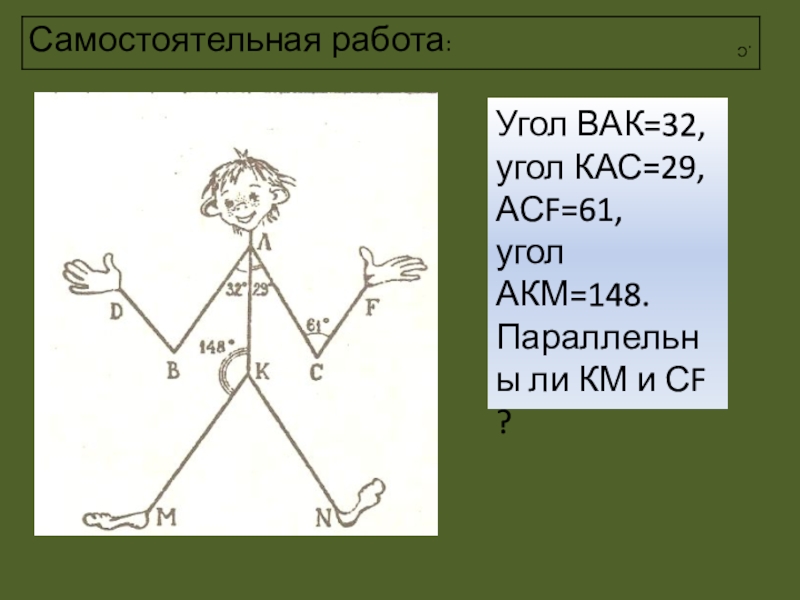
- 18. .СУгол ВАК=32, угол КАС=29, АСF=61, угол АКМ=148.Параллельны ли КМ и СF ?
- 19. Дома:П. 24 -29 повторить.задача по рисунку.
- 20. Критерии оценивания за урок:Расшифровка анаграммы 7 баллов.
Цели:Систематизировать знания по теме : признаки параллельности прямых. Понимать, когда необходимо применять признаки параллельности двух прямых, а когда – свойства параллельности прямых при решении задач. развивать логическое мышление.
Слайд 2Цели:
Систематизировать знания по теме : признаки параллельности прямых.
Понимать, когда необходимо
применять признаки параллельности двух прямых, а когда – свойства параллельности прямых при решении задач.
развивать логическое мышление.
развивать логическое мышление.
Слайд 4Закончить предложение:
Параллельными прямыми….
Перпендикулярными называются прямыми,….
Если прямые перпендикулярны третьей, то они….
Аксиома
– это утверждение, которое ….
Теорема – это утверждение, которое ….
Теорема – это утверждение, которое ….
Слайд 5Ответы :
Называются прямые, которые не пересекаются.
При пересечении образуют прямые углы.
Параллельны.
Не требует
доказательство.
Доказывается, используя аксиомы, следствия, свойства , раннее изученные теоремы
Доказывается, используя аксиомы, следствия, свойства , раннее изученные теоремы
Слайд 7 Решение задач.
Как называются углы, образованные двумя прямыми и секущей?
Как называются эти углы: <4 и <5; <4 и <6; <8 и <3; <1 и <6; <4 и <3; <7 и <5; <3 и <5; <2 и <5?
Слайд 121)Вычеркнуть лишние слова в скобках:
Аксиома – это (очевидные, принятые, исходные) положения
геометрии, не требующие (объяснений, доказательств, обоснований).
2) Выбрать окончание формулировки аксиомы параллельных прямых:
Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая, параллельная данной;
б) всегда проходит прямая, параллельная данной;
в) только одна прямая, не пересекающаяся с данной.
3) Что может быть следствием аксиомы или теоремы? Указать неверные ответы.
а) Утверждение, не требующее доказательства.
б) Новая теорема, для доказательства которой использована аксиома или теорема.
в) Утверждение, непосредственно выводимое из аксиомы или теоремы.
2) Выбрать окончание формулировки аксиомы параллельных прямых:
Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая, параллельная данной;
б) всегда проходит прямая, параллельная данной;
в) только одна прямая, не пересекающаяся с данной.
3) Что может быть следствием аксиомы или теоремы? Указать неверные ответы.
а) Утверждение, не требующее доказательства.
б) Новая теорема, для доказательства которой использована аксиома или теорема.
в) Утверждение, непосредственно выводимое из аксиомы или теоремы.
Слайд 135) Указать правильный ответ на вопрос.
Если через точку, лежащую вне прямой.
Проведено несколько прямых, то сколько из них пересекаются с исходной прямой?
а) Неизвестно, так как не сказано, сколько прямых проведено через точку.
б) Все, кроме параллельной прямой.
в) Все, которые имеют на рисунке точку пересечения с исходной прямой.
а) Неизвестно, так как не сказано, сколько прямых проведено через точку.
б) Все, кроме параллельной прямой.
в) Все, которые имеют на рисунке точку пересечения с исходной прямой.
Слайд 146) Почему, если одна из прямых, проходящих через точку, лежащую вне
заданной прямой, параллельна этой прямой, то другие прямые, проходящие через эту точку, не могут быть ей параллельны? Указать неправильный ответ на этот вопрос.
а) Это противоречит аксиоме параллельных прямых.
б) Любая другая пряма,. если она также параллельна заданной, совпадает с первой.
в) Все другие прямые имеют точку пересечения с заданной прямой, хотя она может находиться на сколь угодно большом расстоянии от исходной точки
а) Это противоречит аксиоме параллельных прямых.
б) Любая другая пряма,. если она также параллельна заданной, совпадает с первой.
в) Все другие прямые имеют точку пересечения с заданной прямой, хотя она может находиться на сколь угодно большом расстоянии от исходной точки
Слайд 157. Сколько углов образуется при пересечении двух параллельных прямых третьей?
1) 4.
2) 6. 3) 8. 4) 12.
8. Сколько равных острых углов может образоваться при пересечении двух параллельных прямых третьей?
1) 2. 2) 4. 3) 6. 4) 8.
9. Сколько равных тупых углов может образоваться при пересечении двух параллельных прямых третьей?
1) 2. 2) 4. 3) 8 4) 16.
10. Сколько прямых углов может образоваться при пересечении двух параллельных прямых третьей?
1) 0 2) 2. 3) 4. 4) 8.
8. Сколько равных острых углов может образоваться при пересечении двух параллельных прямых третьей?
1) 2. 2) 4. 3) 6. 4) 8.
9. Сколько равных тупых углов может образоваться при пересечении двух параллельных прямых третьей?
1) 2. 2) 4. 3) 8 4) 16.
10. Сколько прямых углов может образоваться при пересечении двух параллельных прямых третьей?
1) 0 2) 2. 3) 4. 4) 8.
Слайд 1611. При пересечении двух параллельных прямых третьей один из углов оказался
равным 34°. Найдите наименьший из всех образованных при этом углов.
1) Нельзя определить. 2) 34°. 3) 68°. 4) 146°.
12. При пересечении двух параллельных прямых третьей один из углов оказался равным 112°. Найдите наименьший из всех образованных при этом углов.
1) Нельзя определить. 2) 34°. 3) 68°. 4) 112°.
13. При пересечении двух параллельных прямых третьей один из углов оказался равным 97°. Найдите наименьший из всех образованных при этом углов.
1) 97°. 2) 83°. 3) 77°. 4) 7°.
1) Нельзя определить. 2) 34°. 3) 68°. 4) 146°.
12. При пересечении двух параллельных прямых третьей один из углов оказался равным 112°. Найдите наименьший из всех образованных при этом углов.
1) Нельзя определить. 2) 34°. 3) 68°. 4) 112°.
13. При пересечении двух параллельных прямых третьей один из углов оказался равным 97°. Найдите наименьший из всех образованных при этом углов.
1) 97°. 2) 83°. 3) 77°. 4) 7°.
Слайд 20Критерии оценивания за урок:
Расшифровка анаграммы 7 баллов.
Закончи предложение 5 баллов.
Тест 13 баллов
Решение задач 4 баллов.
Задача по рисунку 5 баллов .
Всего 34 баллов.
28-34 баллов оценка «5»
22-27баллов оценка «4»
17-21 баллов оценка «3»