- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема Пифагора в разных странах.
Содержание
- 1. Теорема Пифагора в разных странах.
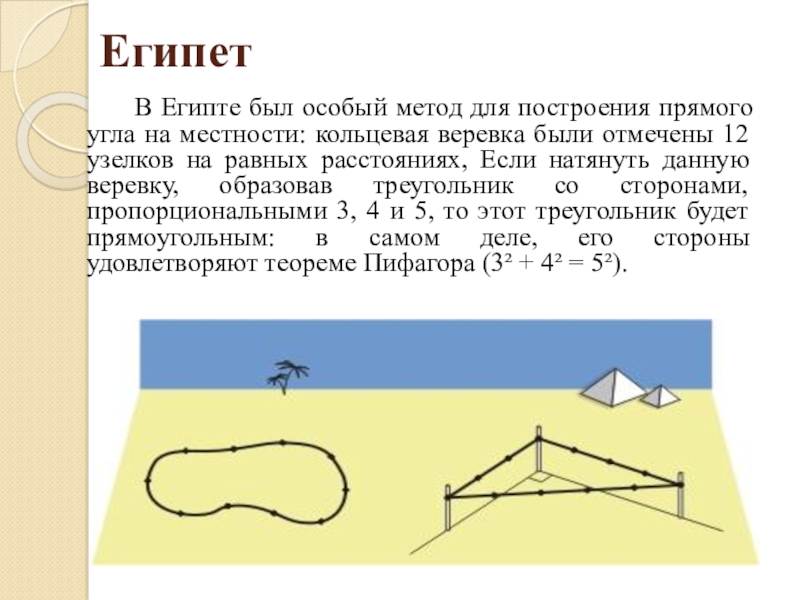
- 2. Египет В Египте был особый метод для построения
- 3. Вавилон Вавилоняне еще в середине II тысячелетия до
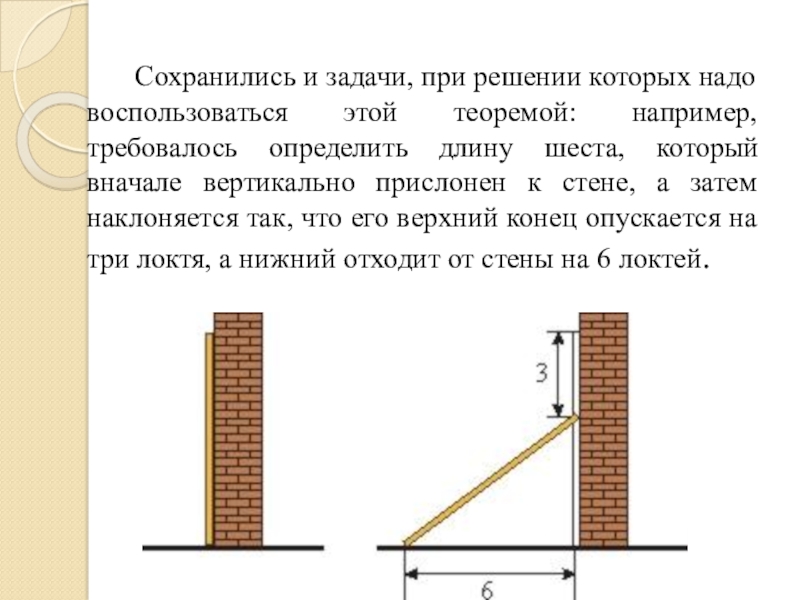
- 4. Сохранились и задачи, при решении которых надо
- 5. Китай Согласно китайскому «Трактату об измерительном шесте», теорема
- 6. Значит, квадрат гипотенузы равен большому квадрату, уменьшенному
- 7. В Китае теорема Пифагора называлась правилом «гоу-гу»:
- 8. В самом трактате «Математика в девяти книгах»
- 9. Индия В Индии теорема Пифагора была известна уже
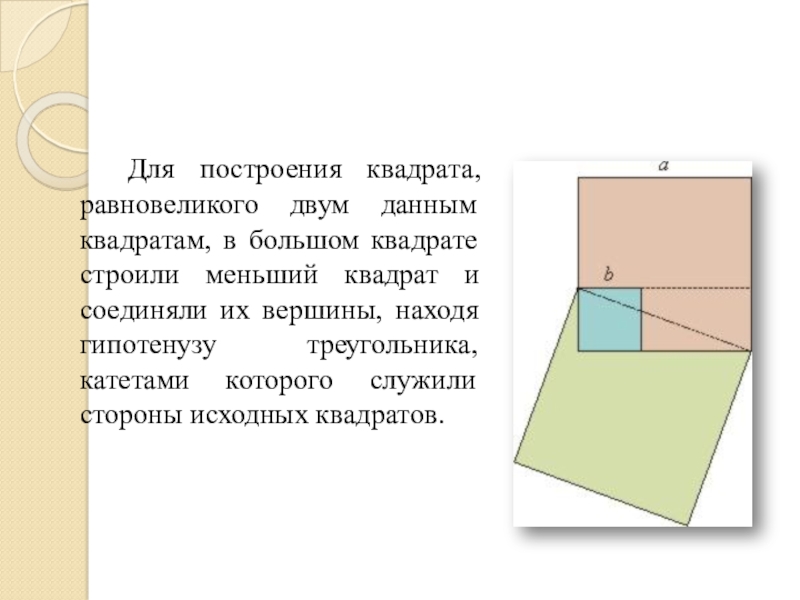
- 10. Для построения квадрата, равновеликого двум данным квадратам,
- 11. Доказательство теоремы Пифагора приводится в книге «Венец
- 12. Греция Вполне вероятно, что в Греции теорему
- 13. Доказательство. Квадрат на левом катете ABFH
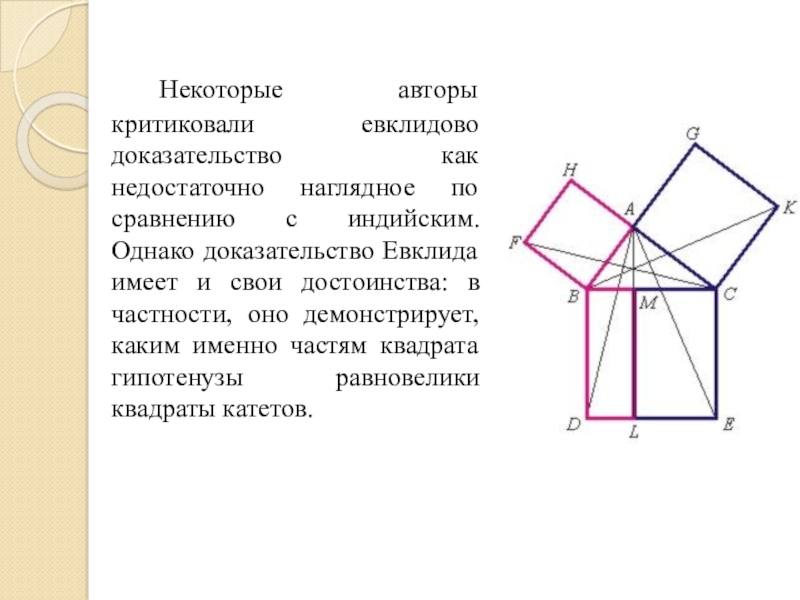
- 14. Некоторые авторы критиковали евклидово доказательство как недостаточно
Слайд 1Теорема Пифагора в разных странах мира
Презентацию подготовил
ученик 8 А класса
средней школы
Ронжин Алексей
Учитель:
Бояхчян Наталья Евгеньевна
Рязань, 2015 г.
Слайд 2Египет
В Египте был особый метод для построения прямого угла на местности:
Слайд 3Вавилон
Вавилоняне еще в середине II тысячелетия до н. э. знали, что
Слайд 4 Сохранились и задачи, при решении которых надо воспользоваться этой теоремой: например,
Слайд 5Китай
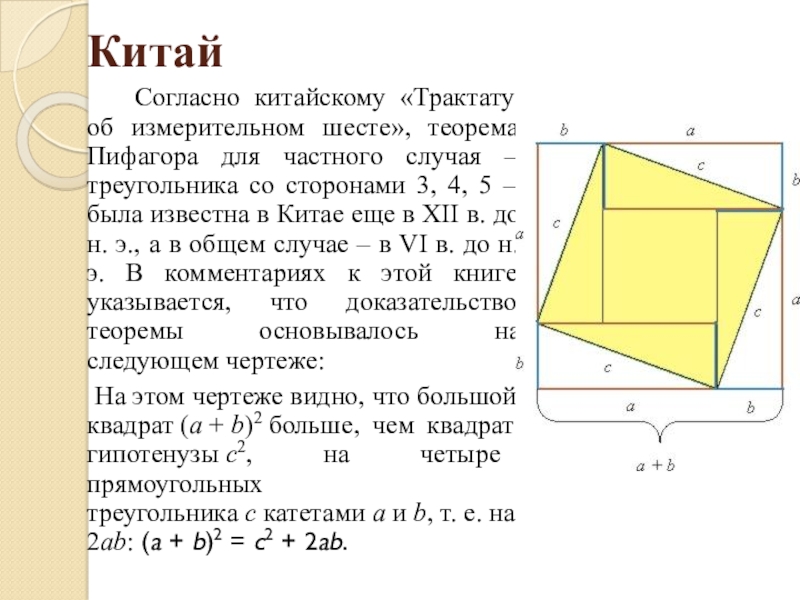
Согласно китайскому «Трактату об измерительном шесте», теорема Пифагора для частного случая
На этом чертеже видно, что большой квадрат (a + b)2 больше, чем квадрат гипотенузы c2, на четыре прямоугольных треугольника c катетами a и b, т. е. на 2ab: (a + b)2 = c2 + 2ab.
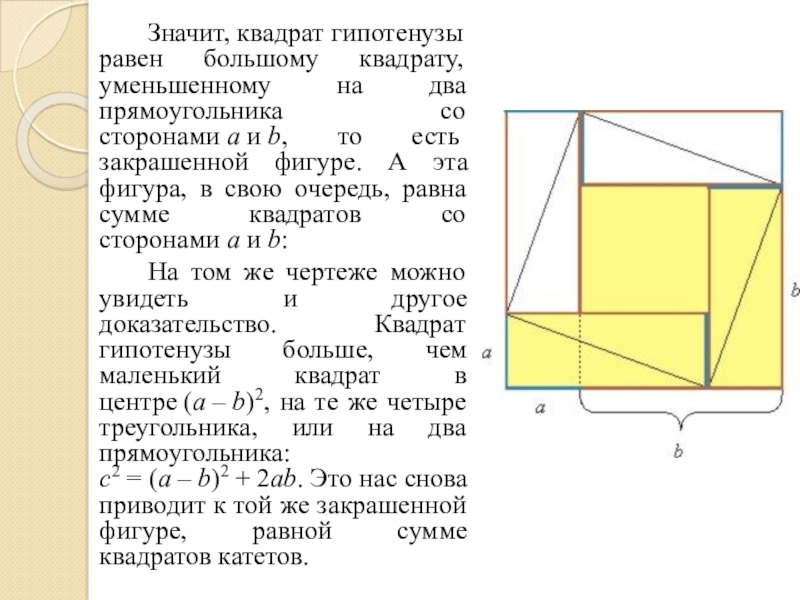
Слайд 6 Значит, квадрат гипотенузы равен большому квадрату, уменьшенному на два прямоугольника со
На том же чертеже можно увидеть и другое доказательство. Квадрат гипотенузы больше, чем маленький квадрат в центре (a – b)2, на те же четыре треугольника, или на два прямоугольника: c2 = (a – b)2 + 2ab. Это нас снова приводит к той же закрашенной фигуре, равной сумме квадратов катетов.
Слайд 7 В Китае теорема Пифагора называлась правилом «гоу-гу»: термины «гоу» (исходно «крюк»)
Имеется водоем со стороной в 1 чжан (10 чи). В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша?
Слайд 8 В самом трактате «Математика в девяти книгах» решение не дается, приводится
То есть, в алгебраических обозначениях, если сторона водоема равна 2a (10 чи), а надводная часть b (1 чи), то глубина водоема равна
(a2 – b2) / 2b, а длина камыша (((a2 – b2) / 2b) + b).
Слайд 9Индия
В Индии теорема Пифагора была известна уже в VII–V вв. до
Слайд 10 Для построения квадрата, равновеликого двум данным квадратам, в большом квадрате строили
Слайд 11 Доказательство теоремы Пифагора приводится в книге «Венец астрономического учения». Собственно, все
Бхаскара приводит ряд задач на применение теоремы Пифагора, похожих на задачи «Математики в девяти книгах». Среди них и задача о водоеме – в индийском варианте в ней вместо камыша фигурирует лотос.
Слайд 12Греция
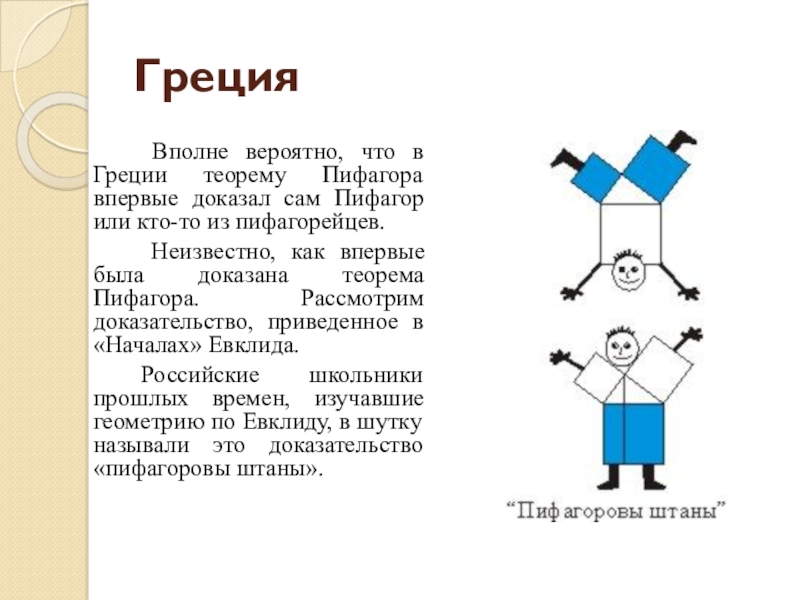
Вполне вероятно, что в Греции теорему Пифагора впервые доказал сам
Неизвестно, как впервые была доказана теорема Пифагора. Рассмотрим доказательство, приведенное в «Началах» Евклида.
Российские школьники прошлых времен, изучавшие геометрию по Евклиду, в шутку называли это доказательство «пифагоровы штаны».
Слайд 13 Доказательство.
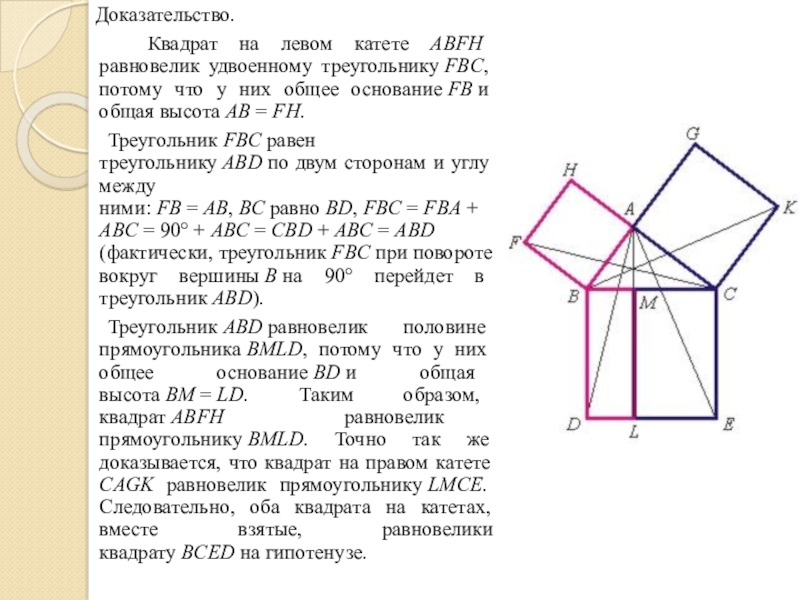
Квадрат на левом катете ABFH равновелик удвоенному треугольнику FBC, потому
Треугольник FBC равен треугольнику ABD по двум сторонам и углу между ними: FB = AB, BC равно BD, FBC = FBA + ABC = 90° + ABC = CBD + ABC = ABD (фактически, треугольник FBC при повороте вокруг вершины B на 90° перейдет в треугольник ABD).
Треугольник ABD равновелик половине прямоугольника BMLD, потому что у них общее основание BD и общая высота BM = LD. Таким образом, квадрат ABFH равновелик прямоугольнику BMLD. Точно так же доказывается, что квадрат на правом катете CAGK равновелик прямоугольнику LMCE. Следовательно, оба квадрата на катетах, вместе взятые, равновелики квадрату BCED на гипотенузе.