Викладач Колієва З.І.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентація з математики на тему Похідна функції її геометричний та фізичний зміст
Содержание
- 1. Презентація з математики на тему Похідна функції її геометричний та фізичний зміст
- 2. Мета уроку: домогтися засвоєння означення похідної; сформувати
- 3. Фронтальне опитуванняДайте означення границі функції в точці.Дайте
- 4. План вивчення темиОзначення похідної функції в точці
- 5. Означення похідної
- 6. Алгоритм для знаходження похідної функції у=f(x) за означенням
- 7. Похідні основних функцій
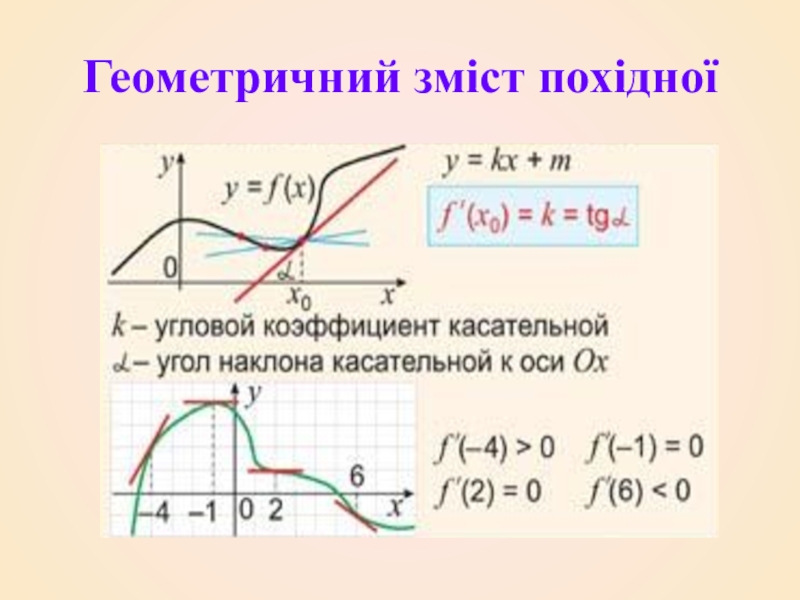
- 8. Геометричний зміст похідної
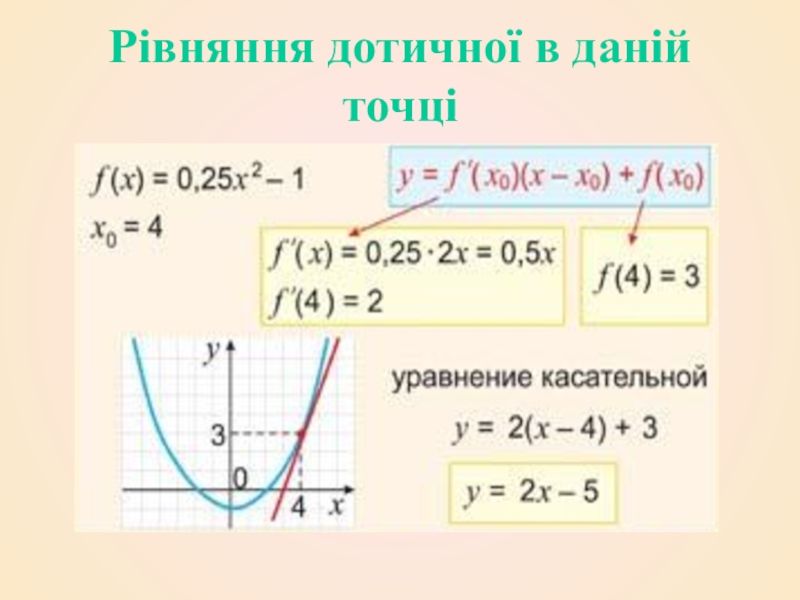
- 9. Рівняння дотичної в даній точці
- 10. Виконання письмових вправ
- 11. Підсумки уроку1. Що називається похідною функції в
- 12. Домашнє завданняР. 2. п.7 вивчити конспект Самостійна робота с.77
Мета уроку: домогтися засвоєння означення похідної; сформувати значення похідної під час обґрунтування формул для обчислення похідних деяких функцій;сформувати поняття похідної в точці, операція диференціюваннязагальна схема знаходження похідної в заданій точці; сформувати геометричний та фізичний зміст
Слайд 1Урок № 3
Тема уроку: « Похідна функції її геометричний та фізичний
зміст»
Слайд 2Мета уроку:
домогтися засвоєння означення похідної;
сформувати значення похідної під час
обґрунтування формул для обчислення похідних деяких функцій;
сформувати поняття похідної в точці, операція диференціювання
загальна схема знаходження похідної в заданій точці;
сформувати геометричний та фізичний зміст похідної;
сформувати вміння знаходити кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці,знайти швидкість зміни величини в точці.
сформувати поняття похідної в точці, операція диференціювання
загальна схема знаходження похідної в заданій точці;
сформувати геометричний та фізичний зміст похідної;
сформувати вміння знаходити кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці,знайти швидкість зміни величини в точці.
Слайд 3Фронтальне опитування
Дайте означення границі функції в точці.
Дайте означення функції неперервної на
проміжку?
Сформулюйте властивості границі функції.
Сформулюйте означення дотичної до кола.
Запишіть рівняння прямої.
Що таке кутовий коефіцієнт прямої? Чому дорівнює кутовий коефіцієнт прямої:
а) яка є бісектрисою І і ІІІ координатних кутів;
б) яка є бісектрисою ІІ і ІV координатних кутів;
в) паралельна осі абсцис?
Сформулюйте властивості границі функції.
Сформулюйте означення дотичної до кола.
Запишіть рівняння прямої.
Що таке кутовий коефіцієнт прямої? Чому дорівнює кутовий коефіцієнт прямої:
а) яка є бісектрисою І і ІІІ координатних кутів;
б) яка є бісектрисою ІІ і ІV координатних кутів;
в) паралельна осі абсцис?
Слайд 4План вивчення теми
Означення похідної функції в точці хо .
Яка функція називається
диференційованою в точці? на проміжку?
Схема знаходження похідної функції f(x) за означенням .
Використання означення під час обґрунтування формул для обчислення похідних деяких функцій.
Зв'язок між диференційованістю та неперервністю функцій.
Геометричний зміст похідної. Кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці
Фізичний зміст похідної. Швидкість та прискорення прямолінійного руху.
Схема знаходження похідної функції f(x) за означенням .
Використання означення під час обґрунтування формул для обчислення похідних деяких функцій.
Зв'язок між диференційованістю та неперервністю функцій.
Геометричний зміст похідної. Кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці
Фізичний зміст похідної. Швидкість та прискорення прямолінійного руху.
Слайд 11Підсумки уроку
1. Що називається похідною функції в точці хо .
2.Яка функція
називається диференційованою в точці? на проміжку?
3.Схема знаходження похідної функції f(x) за означенням .
4.Геометричний зміст похідної. Кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці
5.Фізичний зміст похідної. Швидкість та прискорення прямолінійного руху.
3.Схема знаходження похідної функції f(x) за означенням .
4.Геометричний зміст похідної. Кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці
5.Фізичний зміст похідної. Швидкість та прискорення прямолінійного руху.