- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта по математике на тему Энциклопедия теоремы Пифагора(8 класс)
Содержание
- 1. Презентация проекта по математике на тему Энциклопедия теоремы Пифагора(8 класс)
- 2. Актуальность темы«Пребудет вечной истина, как скороЕё познает
- 3. ГИПОТЕЗА Была бы в геометрии красота, если бы не было вдохновения?
- 4. Цель: познакомиться с различными доказательствами теоремы Пифагора.
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
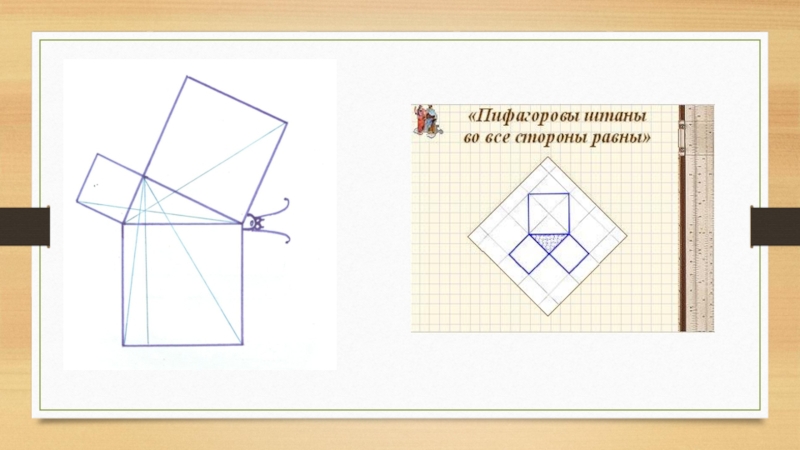
- 9. СПОСОБ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ПИФАГОРА БЕЗ СЛОВ
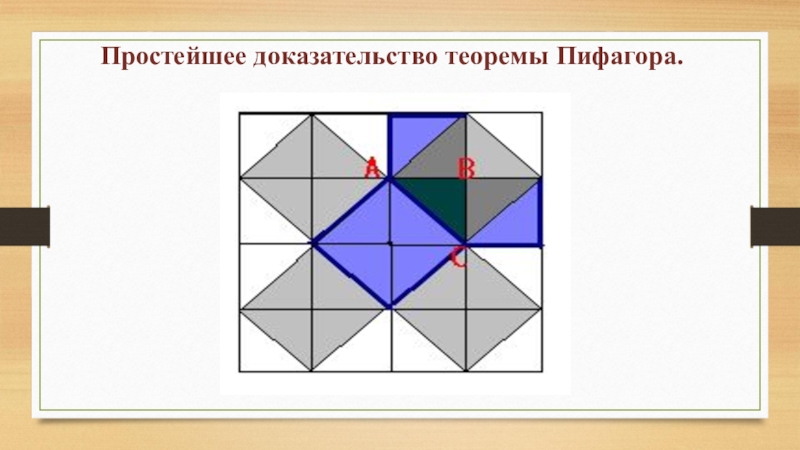
- 10. Простейшее доказательство теоремы Пифагора.
- 11. Геометрическое доказательствоПостройте прямоугольный треугольник ABC. Нам надо
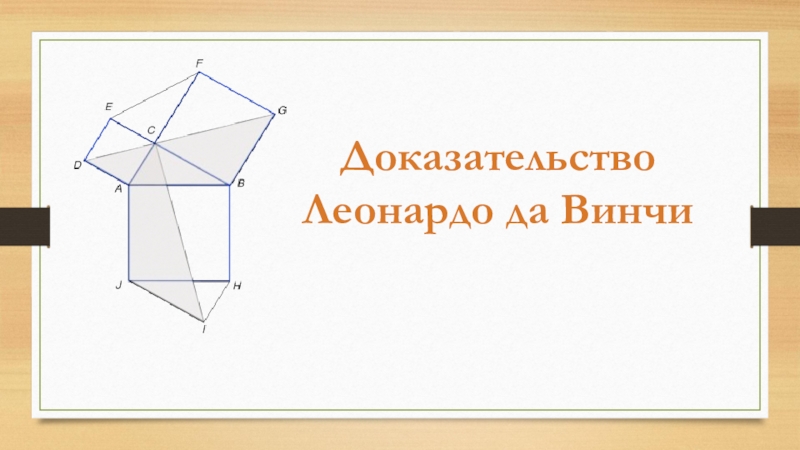
- 12. ДоказательствоЛеонардо да Винчи
- 13. Строительство
- 14. МОЛНИЕОТВОДПо теореме Пифагора h2 ≥ a2+b2
- 15. Собор Парижской Богоматери красив и прочен благодаря геометрии в частности, расчётам по теореме Пифагора.
- 16. Задача древних индусовНад озером тихим,С полфута размером
- 17. Решение:Обозначим глубину пруда через х, тогда высота
- 18. Старинная задача из учебника «Арифметика» Леонтия Магницкого.Случися
- 19. Вывод: Я считаю, что труды Пифагора до
Актуальность темы«Пребудет вечной истина, как скороЕё познает слабый человек!И ныне теорема Пифагора вернаКак и в его далёкий век.» А. ШамиссоТеорема Пифагора издавна широко применяется в разных сферах деятельности и практической жизни.
Слайд 1ПРОЕКТ НА ТЕМУ:
«Энциклопедия теоремы Пифагора»
Работу выполнила
Шацких Татьяна
ученица 8б класса
Руководитель Новикова Л.Н.
Слайд 2Актуальность темы
«Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема
Пифагора верна
Как и в его далёкий век.» А. Шамиссо
Как и в его далёкий век.» А. Шамиссо
Теорема Пифагора издавна широко применяется в разных сферах деятельности и практической жизни.
Слайд 4Цель: познакомиться с различными доказательствами теоремы Пифагора. Понять, что геометрия- это
просто. Увидеть красоту в «трудном» школьном предмете. Показать практическое применение теоремы Пифагора в окружающем нас мире.
Задачи:
Выяснить: оправдана ли популярность теоремы Пифагора.
Изучить биографию Пифагора и историю создания теоремы, решение
старинных задач.
Рассмотреть неизвестные нам способы доказательства теоремы и её
использование в строительстве, астрономии, мобильной связи.
Задачи:
Выяснить: оправдана ли популярность теоремы Пифагора.
Изучить биографию Пифагора и историю создания теоремы, решение
старинных задач.
Рассмотреть неизвестные нам способы доказательства теоремы и её
использование в строительстве, астрономии, мобильной связи.
Слайд 11Геометрическое доказательство
Постройте прямоугольный треугольник ABC. Нам надо доказать, что BC2=AC2+AB2.
Для этого
продолжите катет AC и постройте отрезок CD, который равен катету AB. Опустите перпендикулярный AD отрезок ED. Отрезки ED и AC равны. Соедините точки E и B, а также Eи C и получите чертёж, как на рисунке.
Чтобы доказать теорему воспользуемся следующим способом: найдём площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.
Найти площадь многоугольника ABED можно, сложив площади трёх треугольников, которые её образуют. Причём один из них, ECB. Является не только прямоугольным, но и равнобедренным. Не забываем также, что AB=CD, AC=ED и BC=CE – это позволит нам упростить запись.
SABED=2∙1/2 ∙ (AB∙AC)+1/2BC2.
ABED –трапеция. SABED=(DE +AB)∙1/2AD. AD=AC+CD. Приравниваем правые части площадей фигур: AB∙AC +1/2BC2=(DE +AB)∙1/2(AC+CD). Упростим равенство AB∙AC +1/2BC2=1/2AC2 +2∙1/2(AB∙AC)+1/2AB2. В результате преобразований получим BC2 =AC2+AB2.
Чтобы доказать теорему воспользуемся следующим способом: найдём площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.
Найти площадь многоугольника ABED можно, сложив площади трёх треугольников, которые её образуют. Причём один из них, ECB. Является не только прямоугольным, но и равнобедренным. Не забываем также, что AB=CD, AC=ED и BC=CE – это позволит нам упростить запись.
SABED=2∙1/2 ∙ (AB∙AC)+1/2BC2.
ABED –трапеция. SABED=(DE +AB)∙1/2AD. AD=AC+CD. Приравниваем правые части площадей фигур: AB∙AC +1/2BC2=(DE +AB)∙1/2(AC+CD). Упростим равенство AB∙AC +1/2BC2=1/2AC2 +2∙1/2(AB∙AC)+1/2AB2. В результате преобразований получим BC2 =AC2+AB2.
Слайд 15Собор Парижской Богоматери красив и прочен благодаря геометрии в частности, расчётам
по теореме Пифагора.
Слайд 16Задача древних индусов
Над озером тихим,
С полфута размером высился лотоса цвет.
Он рос
одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
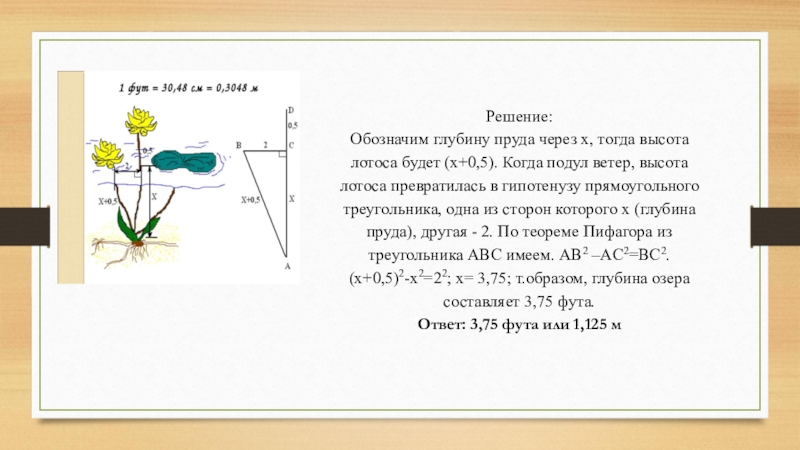
Слайд 17Решение:
Обозначим глубину пруда через х, тогда высота лотоса будет (х+0,5). Когда
подул ветер, высота лотоса превратилась в гипотенузу прямоугольного треугольника, одна из сторон которого х (глубина пруда), другая - 2. По теореме Пифагора из треугольника ABC имеем. AB2 –AC2=BC2.
(x+0,5)2-x2=22; x= 3,75; т.образом, глубина озера составляет 3,75 фута.
Ответ: 3,75 фута или 1,125 м
(x+0,5)2-x2=22; x= 3,75; т.образом, глубина озера составляет 3,75 фута.
Ответ: 3,75 фута или 1,125 м
Слайд 18Старинная задача из учебника «Арифметика» Леонтия Магницкого.
Случися некоему человеку к стене
лестницу прибрати, у стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.
Решение: ВС2=АВ2-АС2; ВС2=15625-13689;
BC=44 стоп.
Ответ: ВС=44 стоп.
Слайд 19Вывод: Я считаю, что труды Пифагора до сих пор актуальны, ведь
куда бы мы ни посмотрели, везде можно увидеть плоды его великих идей, которые воплощены в различные отрасли современной жизни. Значение теоремы состоит в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых.