- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Подготовка к ОГЭ модуль геометрия
Содержание
- 1. Презентация Подготовка к ОГЭ модуль геометрия
- 2. «Аннотация!»- Решая задачи по КИМ-ам ОГЭ по
- 3. Цели:1) Всесторонне исследовать проблему, связанную с решением
- 4. Задачи:1. Научиться решать все виды
- 5. Задача 1: ТрапецииЗадача:Биссектрисы углов А и В
- 6. Задача 2: РомбЗадача:В ромбе ABCD угол DAB
- 7. Задача 3: Решения формулой площади параллелограммаЗадача:Найдите площадь
- 8. Задача 4: Площадь параллелограмма.На клетчатой бумаге с
- 9. Задача 5: Площадь ромба.Найдите площадь ромба, если
- 10. Задача 6: Площадь квадрата.Периметр квадрата равен 32.
- 11. Задача 7: Средняя линия трапеции.На клетчатой бумаге
- 12. Задача 8: Равнобедренная трапеция.Найдите больший угол равнобедренной
- 13. Задача 9: Площадь треугольника.На клетчатой бумаге с
- 14. Задача 10: Площадь параллелограмма.Найдите площадь параллелограммы, изображенного
- 15. Задача 11: Равнобедренная трапеция.Сумма двух углов равнобедренной
- 16. Задача 12: Площадь трапеции.На клетчатой бумаге с
- 17. Задача 13: Площадь параллелограмма.Найдите площадь параллелограмма, изображенного
- 18. Задача 14: Равнобедренная трапеция.В трапеции ABCD известно,
- 19. Справочные материалы.
- 20. Литература и интернет ресурсы:1) И. В. Ященко
- 21. Желаю вам успехов и удачи в подготовкек
«Аннотация!»- Решая задачи по КИМ-ам ОГЭ по геометрии, а именно №11 и №12, выяснилось, что мне необходимо повторить ряд формул и теорем из ранее пройденного материала. Пообщавшись с одноклассниками, выяснилось, что аналогичные вопросы возникают не только
Слайд 2«Аннотация!»
- Решая задачи по КИМ-ам ОГЭ по геометрии, а именно №11
и №12, выяснилось, что мне необходимо повторить ряд формул и теорем из ранее пройденного материала. Пообщавшись с одноклассниками, выяснилось, что аналогичные вопросы возникают не только у меня, но так же и у моих одноклассников. Возникла идея подробно проработать эту проблему и создать банк заданий, который поможет мне и моим одноклассникам успешно справляться с №11 и №12. самостоятельно исследовав в интернет ресурсах необходимый материал, я создал проектную работу, которая, надеюсь, поможет в решении модуля «геометрии». В данном проекте рассмотрены наиболее сложные задачи. Более легкие варианты не вызывали затруднения ни у меня, ни у одноклассников.
Слайд 3Цели:
1) Всесторонне исследовать проблему, связанную с решением задач по геометрии №
11 и №12 по КИМ-ам ОГЭ 2017 г.
2) Успешно сдать ОГЭ по Математике.
2) Успешно сдать ОГЭ по Математике.
Слайд 4
Задачи:
1. Научиться решать все виды заданий № 12 и 11 (на
нахождении площади "S" фигур)
2. Развивать свои навыки логического мышления.
3. Воспитать в себе ответственного отношения к учёбе.
4. Помочь одноклассникам.
2. Развивать свои навыки логического мышления.
3. Воспитать в себе ответственного отношения к учёбе.
4. Помочь одноклассникам.
Слайд 5Задача 1: Трапеции
Задача:
Биссектрисы углов А и В при боковой стороне АВ
трапеции АВСD пересекаются в точке F. Найдите АВ, если AF=24, BF=10.
Сумма углов при боковой стороне трапеции, как известно, равна 180.
Каждая из биссектрис разделит свой угол пополам, поэтому сумма углов FBA и BAF будет равна {180{circ}}/2={90{circ}}, и значит, треугольник BAF – прямоугольный, и его гипотенузу АВ можно определить по теореме Пифагора:
Ответ: 26.
Сумма углов при боковой стороне трапеции, как известно, равна 180.
Каждая из биссектрис разделит свой угол пополам, поэтому сумма углов FBA и BAF будет равна {180{circ}}/2={90{circ}}, и значит, треугольник BAF – прямоугольный, и его гипотенузу АВ можно определить по теореме Пифагора:
Ответ: 26.
Слайд 6Задача 2: Ромб
Задача:
В ромбе ABCD угол DAB равен 36^{\circ}. Найдите угол
BDC. Ответ дайте в градусах.
Решение:
1) По свойству ромба соседние углы в сумме дают 180^{\circ}.
Значит
2) По свойству ромба диагонали являются биссектрисами углов.
Значит,
Ответ: 72.
Решение:
1) По свойству ромба соседние углы в сумме дают 180^{\circ}.
Значит
2) По свойству ромба диагонали являются биссектрисами углов.
Значит,
Ответ: 72.
Слайд 7Задача 3: Решения формулой площади параллелограмма
Задача:
Найдите площадь ромба, если его стороны
равны 1, а один из углов равен 1500.
Используем формулу площади параллелограмма:
Стороны равны 1, а острый угол будет равен 30:
Ответ: 0,5
Используем формулу площади параллелограмма:
Стороны равны 1, а острый угол будет равен 30:
Ответ: 0,5
Слайд 8Задача 4: Площадь параллелограмма.
На клетчатой бумаге с размером клетки 1х1 изображён
параллелограмм. Найдите его площадь.
Решение:
S = ah
a = 5
h = 7
S = 5*7 = 35
Ответ: S=35
Решение:
S = ah
a = 5
h = 7
S = 5*7 = 35
Ответ: S=35
Слайд 9Задача 5: Площадь ромба.
Найдите площадь ромба, если его диагонали равны 8
и 6.
Решение:
S = (8*6)/2 = 24.
Ответ:S = 24.
Решение:
S = (8*6)/2 = 24.
Ответ:S = 24.
Слайд 10Задача 6: Площадь квадрата.
Периметр квадрата равен 32. Найдите площадь этого квадрата.
Решение:
1)
32/4 = 8 – сторона.
2) 8*8 = 64.
Ответ: S = 64.
2) 8*8 = 64.
Ответ: S = 64.
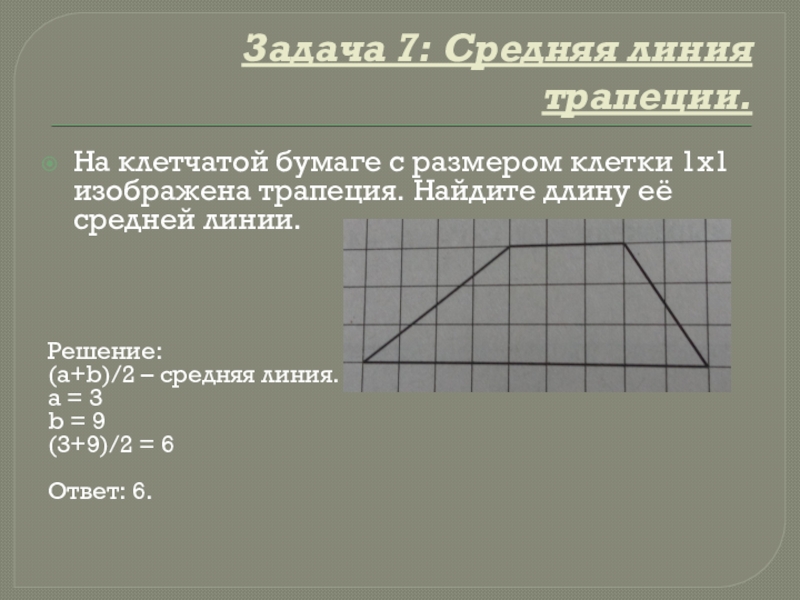
Слайд 11Задача 7: Средняя линия трапеции.
На клетчатой бумаге с размером клетки 1х1
изображена трапеция. Найдите длину её средней линии.
Решение:
(a+b)/2 – средняя линия.
a = 3
b = 9
(3+9)/2 = 6
Ответ: 6.
Решение:
(a+b)/2 – средняя линия.
a = 3
b = 9
(3+9)/2 = 6
Ответ: 6.
Слайд 12Задача 8: Равнобедренная трапеция.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ
AC образует с основанием AD и боковой стороной AB углы, равные 12 и 13 градусов соответственно.
Решение:
Сумма углов 360 гр.
А + В = 180 гр.
1) 12 + 13 = 25.
2) 180 – 25 = 155
Ответ: 155.
Решение:
Сумма углов 360 гр.
А + В = 180 гр.
1) 12 + 13 = 25.
2) 180 – 25 = 155
Ответ: 155.
Слайд 13Задача 9: Площадь треугольника.
На клетчатой бумаге с размером клетки 1х1 изображен
треугольник.
Найдите его площадь.
Решение:
S = (a*h)/2
a = 4
h = 4
1) 4*4 = 16
2) 16/2 = 8
Ответ: S = 8
Найдите его площадь.
Решение:
S = (a*h)/2
a = 4
h = 4
1) 4*4 = 16
2) 16/2 = 8
Ответ: S = 8
Слайд 14Задача 10: Площадь параллелограмма.
Найдите площадь параллелограммы, изображенного на рисунке.
Решение:
S = ah
a
= 12+8 = 20
h = 5
S = 20 * 5 = 100.
Ответ: S = 100
h = 5
S = 20 * 5 = 100.
Ответ: S = 100
Слайд 15Задача 11: Равнобедренная трапеция.
Сумма двух углов равнобедренной трапеции 220 гр. Найдите
меньший угол трапеции.
Решение:
т.к. трапеция равнобедренная, то:
1)220/2 = 110 – больший угол
т.к. сумма боковых углов 180, то:
2) 180 -110 = 70 – меньший угол
Ответ: 70
Решение:
т.к. трапеция равнобедренная, то:
1)220/2 = 110 – больший угол
т.к. сумма боковых углов 180, то:
2) 180 -110 = 70 – меньший угол
Ответ: 70
Слайд 16Задача 12: Площадь трапеции.
На клетчатой бумаге с размером клетки 1х1 изображена
трапеция. Найдите её площадь.
Решение:
S = ((a+b)/2 )* h
1) a = 3, b = 7, h = 3.
2) 3 + 7 = 10
3) 10/2 = 5
4) 5*3 = 15
Ответ: S = 15.
Решение:
S = ((a+b)/2 )* h
1) a = 3, b = 7, h = 3.
2) 3 + 7 = 10
3) 10/2 = 5
4) 5*3 = 15
Ответ: S = 15.
Слайд 17Задача 13: Площадь параллелограмма.
Найдите площадь параллелограмма, изображенного на рисунке.
Решение:
S = ah
a
= 3 + 5 = 8
h = 12
S = 8*12 = 96
S = 96.
h = 12
S = 8*12 = 96
S = 96.
Слайд 18Задача 14: Равнобедренная трапеция.
В трапеции ABCD известно, что AB = CD,
угол BDA = 67 гр. и угол BDC = 28 гр. Найдите угол ABD.
Решение:
1) 67 + 28 = 95 – угол D
Рассмотрим треуг. ABD.
2) 95 + 67 = 162
Сумма углов = 180 гр.
3) 180 – 162 = 18.
Ответ: ABD = 18.
Решение:
1) 67 + 28 = 95 – угол D
Рассмотрим треуг. ABD.
2) 95 + 67 = 162
Сумма углов = 180 гр.
3) 180 – 162 = 18.
Ответ: ABD = 18.
Слайд 20Литература и интернет ресурсы:
1) И. В. Ященко - "ОГЭ 2017 Математика".
(Типовые Экзаменационные варианты).
2) Официальный сайт ФИПИ: http://fipi.ru/
2) Официальный сайт ФИПИ: http://fipi.ru/