- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Равновеликие тела
Содержание
- 1. Презентация по теме: Равновеликие тела
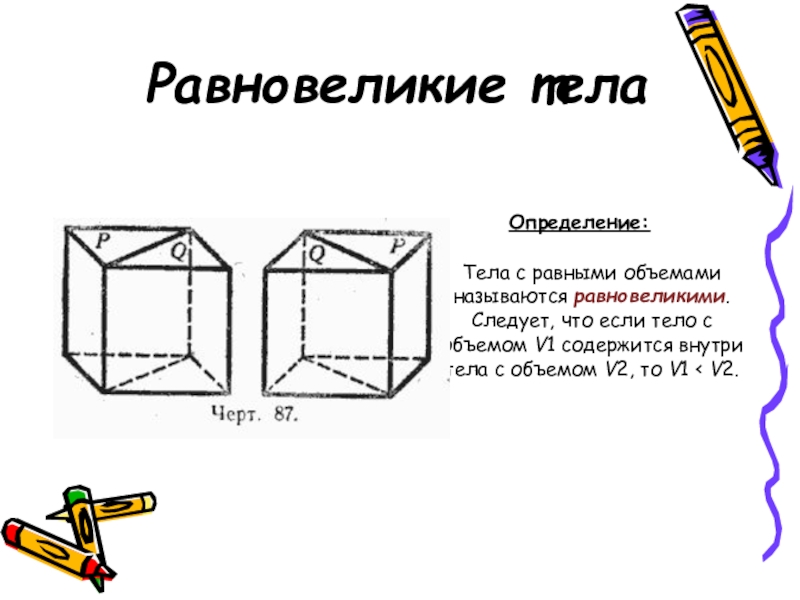
- 2. Равновеликие телаОпределение:Тела с равными объемами называются равновеликими.
- 3. Пространство, занимаемое каким-нибудь телом, или вместимость этого тела называется его объемом.
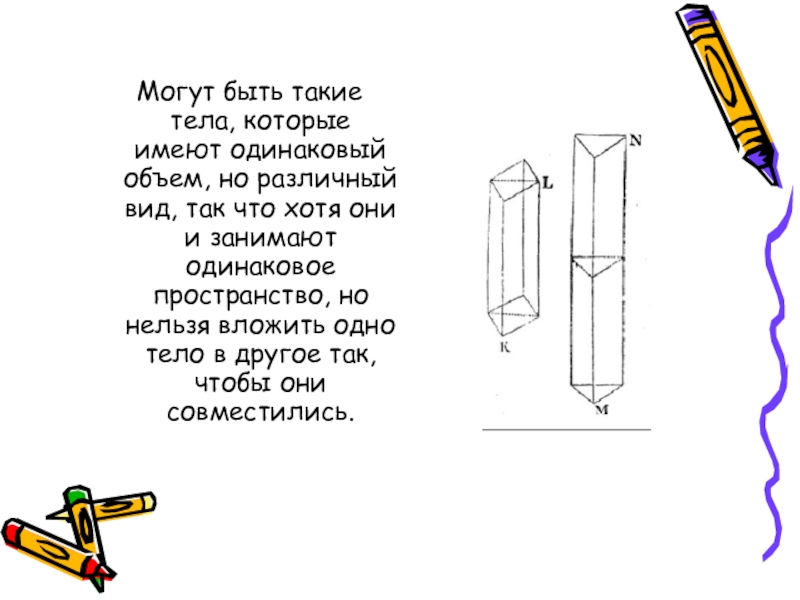
- 4. Могут быть такие тела, которые имеют
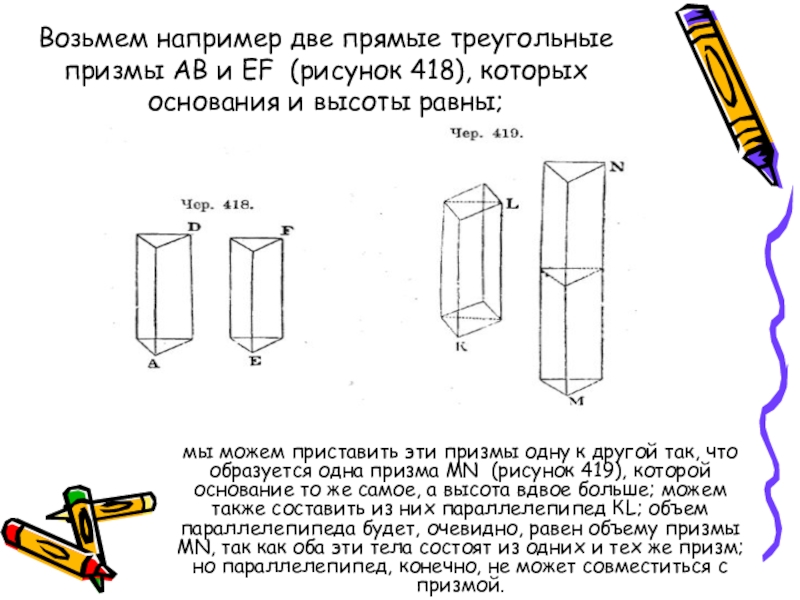
- 5. Возьмем например две прямые треугольные призмы АВ
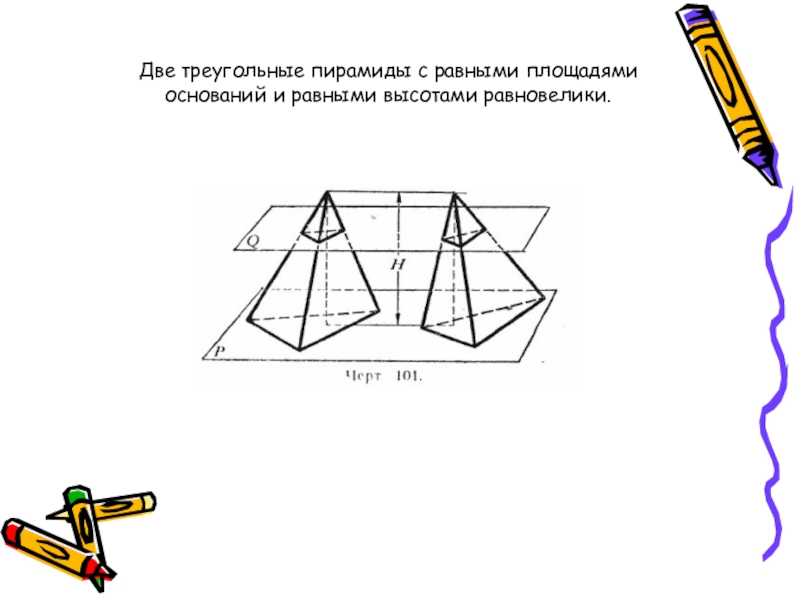
- 6. Две треугольные пирамиды с равными площадями оснований и равными высотами равновелики.
- 7. Действительно, пусть треугольные пирамиды имеют равные площади
- 8. Разделим высоту каждой пирамиды на п равных
- 9. Это неравенство выполняется при любом сколь угодно
Слайд 2Равновеликие тела
Определение:
Тела с равными объемами называются равновеликими. Следует, что если тело
Слайд 3Пространство, занимаемое каким-нибудь телом, или вместимость этого тела называется его объемом.
Слайд 4 Могут быть такие тела, которые имеют одинаковый объем, но различный
Слайд 5Возьмем например две прямые треугольные призмы АВ и ЕF (рисунок 418), которых
мы можем приставить эти призмы одну к другой так, что образуется одна призма МN (рисунок 419), которой основание то же самое, а высота вдвое больше; можем также составить из них параллелепипед КL; объем параллелепипеда будет, очевидно, равен объему призмы MN, так как оба эти тела состоят из одних и тех же призм; но параллелепипед, конечно, не может совместиться с призмой.
Слайд 7Действительно, пусть треугольные пирамиды имеют равные площади оснований и равные высоты.
Слайд 8Разделим высоту каждой пирамиды на п равных частей и проведем через
Пусть V1 и V2 — объемы пирамид, a V`и V`2 — суммы объемов построенных для них призм. Так как объем призмы в k-m слое первой пирамиды равен объему призмы {к - 1)-го слоя второй пирамиды, то сумма объемов всех призм для первой пирамиды равна сумме объемов призм всех слоев второй пирамиды, кроме последнего.
Объем призмы последнего слоя равен S—, где S — площадь основания пирамиды, а Н — высота. Отсюда следует, что
V'1 =V`2 – S (H\n) • Так как> кроме того, V1 > V'v a V2 < V2,
то V1 > V2 - S^-, или V2- V1 < S^
Слайд 9Это неравенство выполняется при любом сколь угодно большом п. А это
Утверждение доказано.