:
Панченко Андрей, 8«А» класс
МБОУ города Ростова-на-Дону «Лицей №51
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Нахождение площадей фигур на линованной в клетку плоскости
Содержание
- 1. Презентация по теме Нахождение площадей фигур на линованной в клетку плоскости
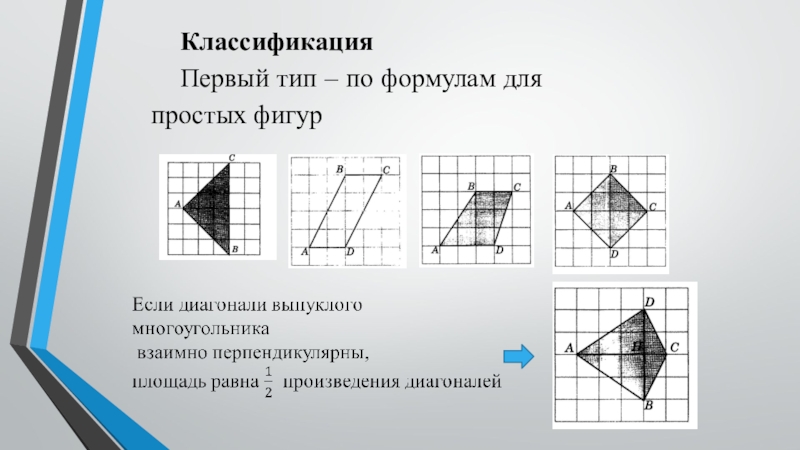
- 2. Классификация Первый тип – по формулам для простых фигур
- 3. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
- 4. Найдите площадь трапеции ABCD, считая стороны квадратных
- 5. Классификация Первый тип – по формулам для простых фигур
- 6. Найдите площадь четырехугольника ABCD, считая стороны квадратных
- 7. Можно разбить данную фигуру на три треугольника
- 8. Найдите площадь ромба ABCD, считая стороны квадратных клеток равными 1.
- 9. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. Второе решение!
- 10. Найдите площадь S сектора, считая стороны квадратных
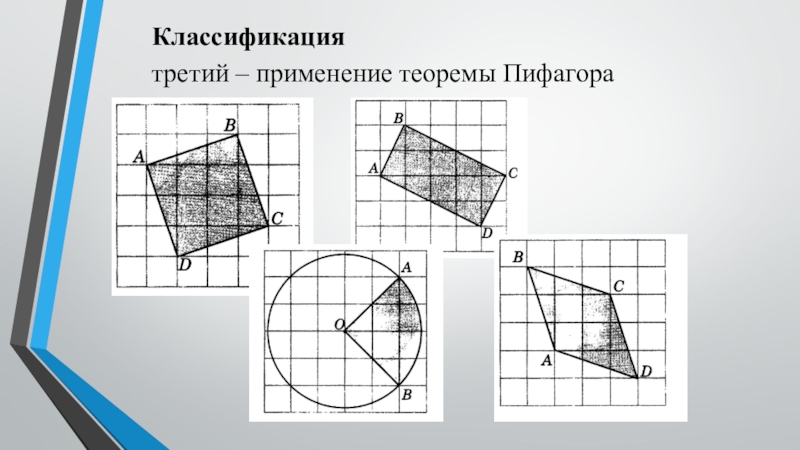
- 11. Классификациятретий – применение теоремы Пифагора
- 12. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. Первое решение!
- 13. Площадь данной фигуры можно вычислить при помощи
- 14. Классификация пятый тип– комбинированный.1234
- 15. Формулу Пика удобно применять для нахождения площадей
- 16. 1. Рабочей тетради Смирнова В.А. «Планиметрия: площади»
- 17. Удачи на экзаменах!
Классификация Первый тип – по формулам для простых фигур
Слайд 4Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
Решение 1. Основания AD и BC данной трапеции равны соответственно 4 и 2. Высотой является боковая сторона CD. Она равна 3. Так как площадь трапеции равна произведению полусуммы оснований на высоту, то площадь данной трапеции будет равна 9.
Слайд 6Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
Решение
3. Диагонали четырехугольника взаимно перпендикулярны
и равны по 4 , значит, площадь равна (4·4):2=8
и равны по 4 , значит, площадь равна (4·4):2=8
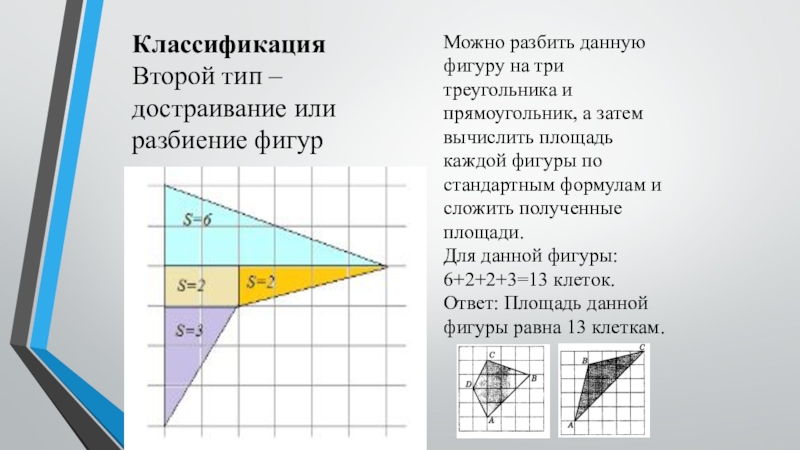
Слайд 7Можно разбить данную фигуру на три треугольника и прямоугольник, а затем
вычислить площадь каждой фигуры по стандартным формулам и сложить полученные площади.
Для данной фигуры: 6+2+2+3=13 клеток. Ответ: Площадь данной фигуры равна 13 клеткам.
Для данной фигуры: 6+2+2+3=13 клеток. Ответ: Площадь данной фигуры равна 13 клеткам.
Классификация
Второй тип – достраивание или разбиение фигур
Слайд 9Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Второе
решение!
Слайд 12Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Первое
решение!
Слайд 13Площадь данной фигуры можно вычислить при помощи формулы Пика.(см. ниже)
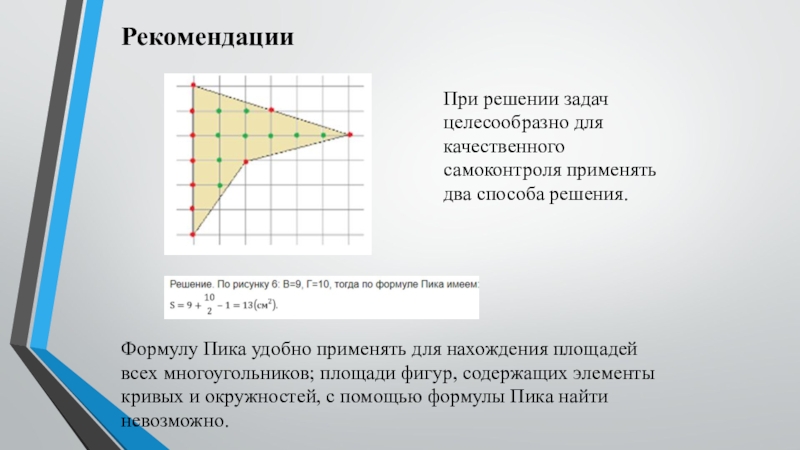
Сосчитаем количество точек внутри и на границе многоугольника. В=9, Г=10. Подставив эти значения в формулу, узнаем площадь данной фигуры. Она равна 13 клеткам. Ответ: Площадь данной фигуры равна 13 клеткам.
Классификация
четвертый –
формула Пика
Слайд 15Формулу Пика удобно применять для нахождения площадей всех многоугольников; площади фигур,
содержащих элементы кривых и окружностей, с помощью формулы Пика найти невозможно.
Рекомендации
При решении задач целесообразно для качественного самоконтроля применять два способа решения.
Слайд 161. Рабочей тетради Смирнова В.А. «Планиметрия: площади» под редакцией А.Л. Семенова
и И.В. Ященко.
2. Татьяненко А.А., Татьяненко С.А. Вычисление площадей фигур, изображенных на клетчатой бумаге // Юный ученый. – 2016. – №3
3. Материалы презентаций Смирнова В.А., 2010 год
В презентации использованы материалы:
