- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Начальные геометрические сведения (7 класс)
Содержание
- 1. Презентация по теме Начальные геометрические сведения (7 класс)
- 2. Урок 1 «Прямая и отрезок».Урок 2 «Луч
- 3. Урок 1 «Прямая и отрезок»
- 4. Ребята, прежде чем начать изучать геометрию, давайте узнаем, как зародилась эта интереснейшая наука.
- 5. Для первобытных людей важную роль играла форма
- 6. Пирамиды, которые были построены более 5 тыс.
- 7. Издавна люди любили украшать свою одежду, дома.В любом орнаменте прослеживаются геометрические фигуры.
- 8. Геометрия – “geо” – земля, “metreo” –
- 9. Первые геометрические понятия возникли из практических потребностей,
- 10. В 3 веке до н.э. древнегреческий ученый
- 11. Величайшие геометры древности завершили создание античной геометрии.Почти
- 12. Геометрические фигуры и узоры окружают нас везде и всюду:
- 13. Геометрические понятия и определения задействованы во многих областях, например, в компьютерных науках.
- 14. Векторная графика представляет изображение как набор примитивов.
- 15. Растровая графика – изображение состоит из точек
- 16. Фрактальная графика.Фрактал — объект, отдельные элементы которого наследуют свойства родительских структур
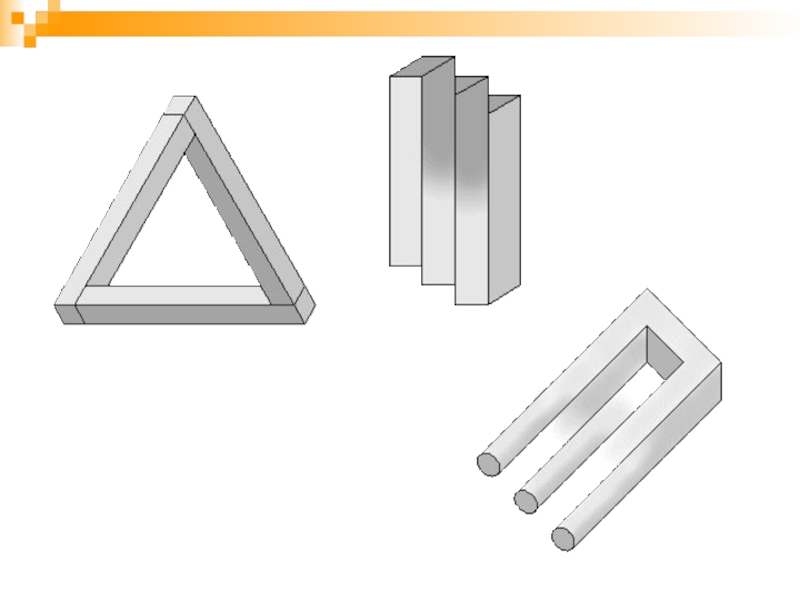
- 17. Невозможные объекты
- 18. Слайд 18
- 19. Морис Корнелиус Эшер «Подъем и спуск»
- 20. Морис Корнелиус Эшер «Водопад»
- 21. Морис Корнелиус Эшер «Белведер»
- 22. Работы Франсиса Табари
- 23. Слайд 23
- 24. Сколько здесь колонн?
- 25. Квадратура колеса
- 26. Окружность в центре кажется искаженной.
- 27. Какая линия длиннее AC или AB?
- 28. Высота фигуры кажется большей чем, чем ее
- 29. А теперь приступим к изучению геометрических понятий.
- 30. ПрямаяЛоманаяОтрезокЛучПрямоугольникКвадратМногоугольникпланиметриястереометрияКакие геометрические фигуры вам известны?КубЦилиндрШарКонусПирамидаПараллелепипед
- 31. а А В Прямую можно обозначить двумя
- 32. а А В D E K C
- 33. «Точка D принадлежит прямой АВ, а точка
- 34. b A B C D E F
- 35. Сколько прямых можно провести через заданную точку?Сколько
- 36. Свойство прямой. Через любые две точки можно
- 37. XYMKOXY ∩ MK = OДве прямые могут
- 38. Отрезок – это часть прямой, ограниченная двумя
- 39. A B C D На прямой а
- 40. №2№5№6Самостоятельно выполните в тетради следующие задания:
- 41. Точка обозначается на плоскости одной большой латинской
- 42. Мой друг изобразил прямую, кривую и ломаную
- 43. § 1, 2, вопросы 1 – 3№
- 44. Урок 2 «Луч и угол»
- 45. Поверим домашнее задание:
- 46. Проверка домашнего задания.№ 3Оabca∩b = O, b∩c
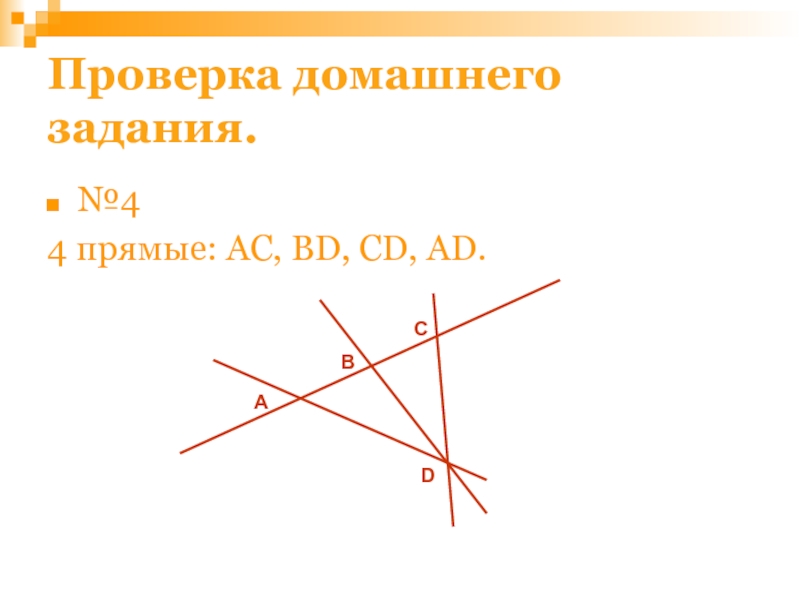
- 47. Проверка домашнего задания.№44 прямые: AC, BD, CD, AD.ABCD
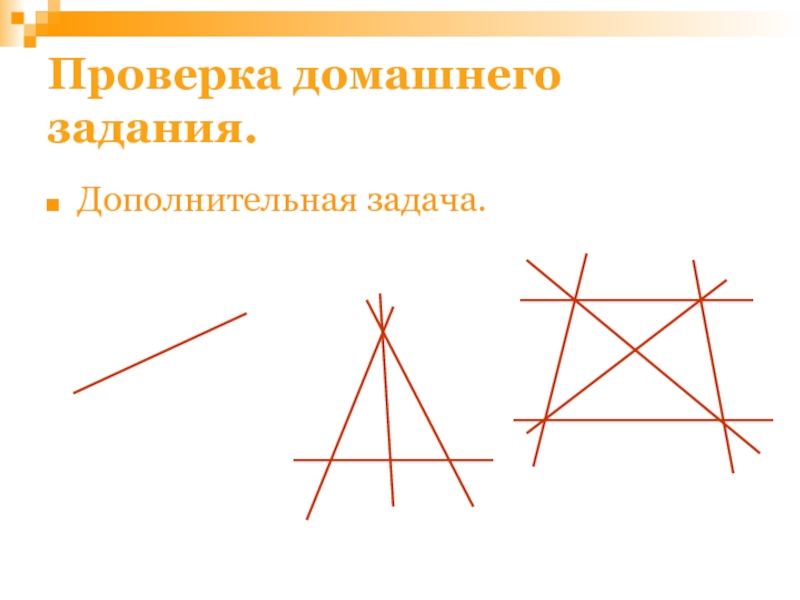
- 48. Дополнительная задача.Проверка домашнего задания.
- 49. Подготовьте ответы на следующие вопросы:Что такое точка?Как
- 50. Выполните самостоятельную работу.1 вариант2 вариантВыпишите точки,
- 51. ОВалучначало лучаПроведите прямую а и отметьте на
- 52. EKCABаABCDНазовите лучи, изображенные на рисунке.
- 53. AKBEСколько лучей, выходящих из точки А, изображено
- 54. Угол – это геометрическая фигура, состоящая из точки и исходящих из нее двух лучей.вершинасторонасторонаАОВОбозначение:hО
- 55. внутренняя область углавнешняя область углавнешняя область углаАОВАОВвнешняя
- 56. Назовите точки, принадлежащие:внешней области угла;внутренней области угла;сторонам угла.ОАВCFDEGN
- 57. №8№9№10№11Выполни самостоятельно работу в тетради.
- 58. Луч – это часть прямой, ограниченная одной
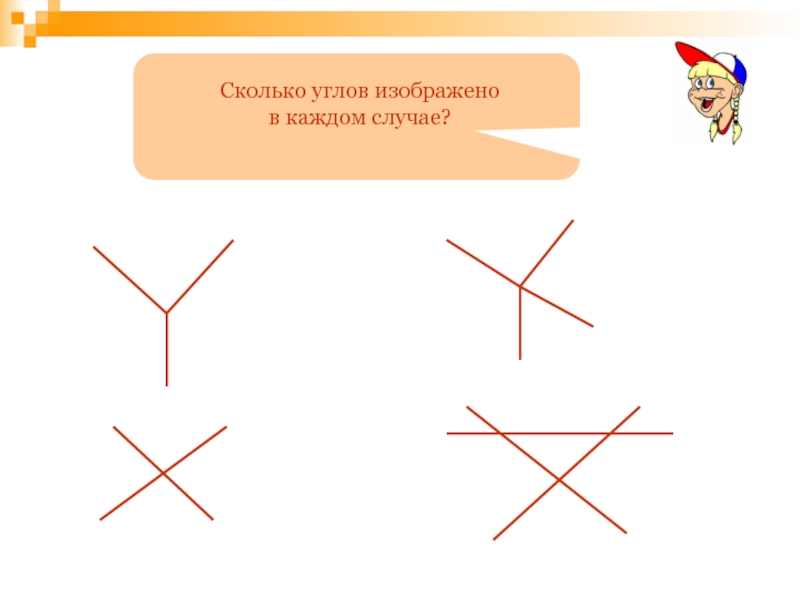
- 59. Сколько углов изображено в каждом случае?
- 60. Какие из лучей, изображенных на рисунке проходят между сторонами развернутого угла ВАС?ВАСabcdfe
- 61. §2, вопросы 2-6№11, 13, 14Дополнительная задача. Сколько существует вариантов расположения трех точек относительно угла?Запишите домашнее задание:
- 62. Урок 3 «Сравнение отрезков и углов»
- 63. Поверим домашнее задание:
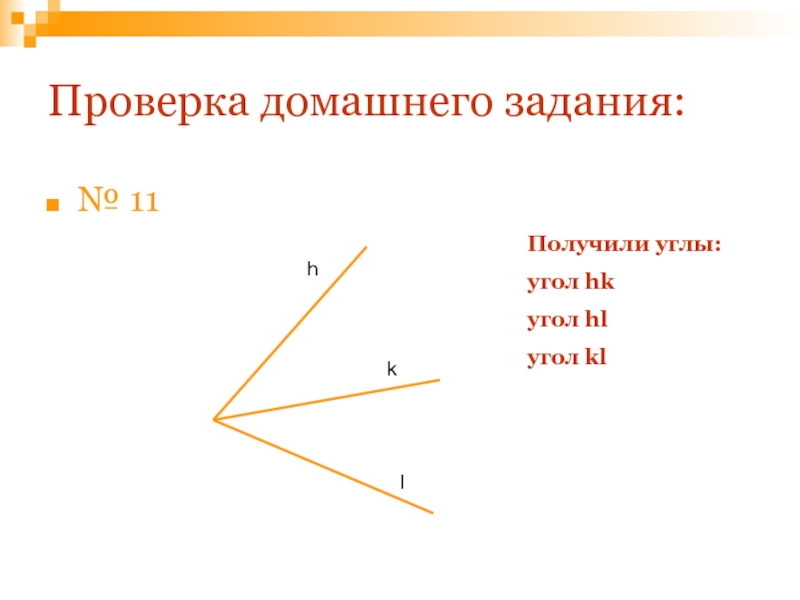
- 64. Проверка домашнего задания:№ 11hklПолучили углы:угол hkугол hlугол kl
- 65. №13Проверка домашнего задания:АВMN
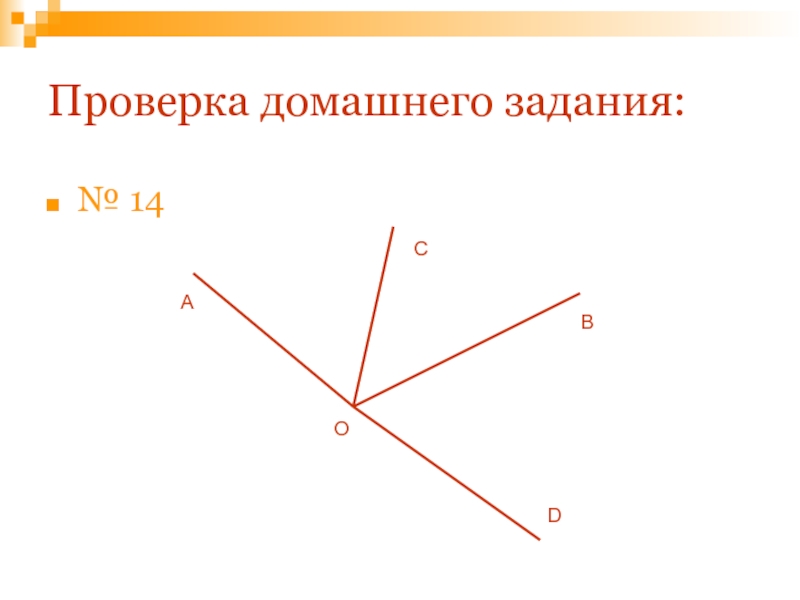
- 66. № 14Проверка домашнего задания:АОВСD
- 67. дополнительная задача
- 68. Подготовьте ответы на следующие вопросы:Что называют лучом?Как
- 69. Какие из данных математических знаков имеют отношение к термину «сравнение»?+∫●≤≥:
- 70. Сравни данные величины и сделай вывод.отрезок АВ=20
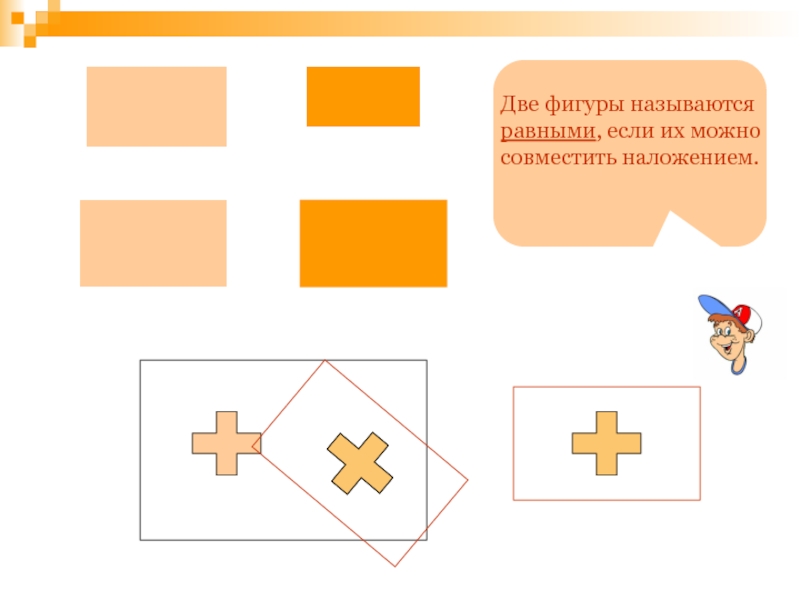
- 71. Две фигуры называются равными, если их можно совместить наложением.
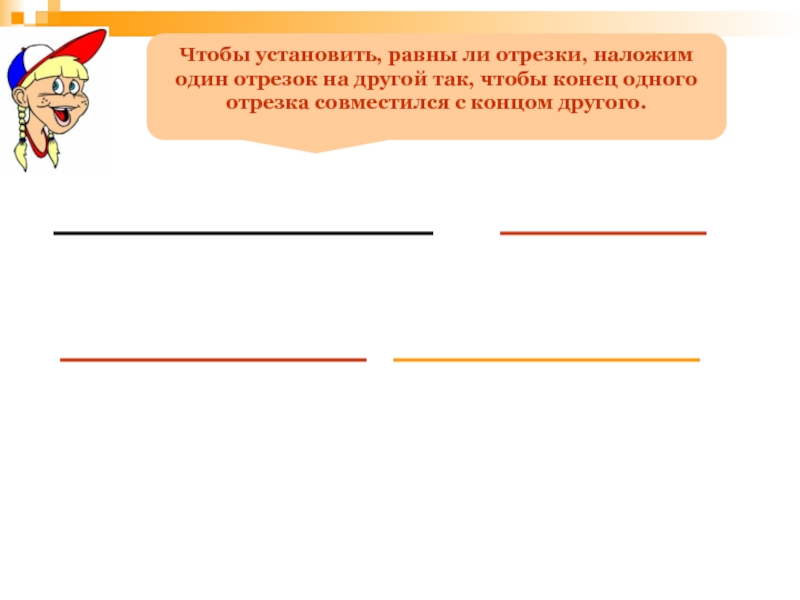
- 72. Чтобы установить, равны ли отрезки, наложим один
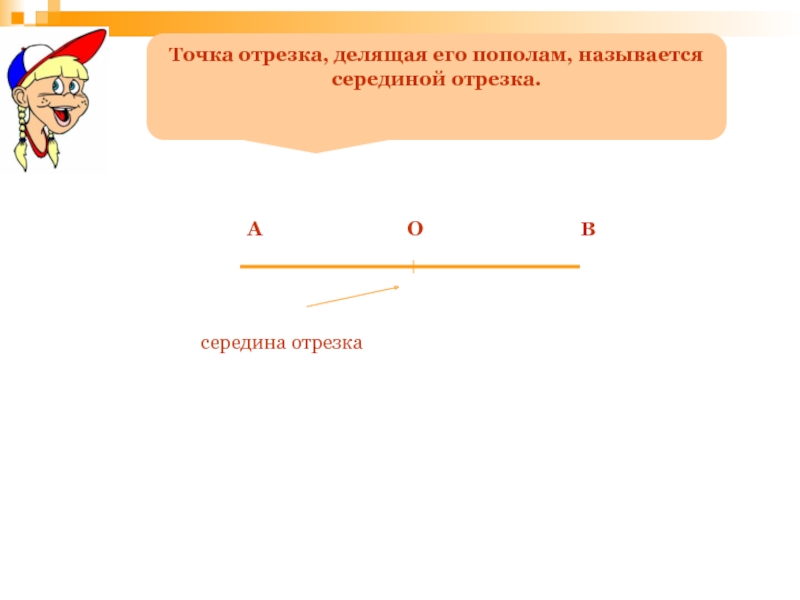
- 73. середина отрезкаТочка отрезка, делящая его пополам, называется серединой отрезка.ОАВ
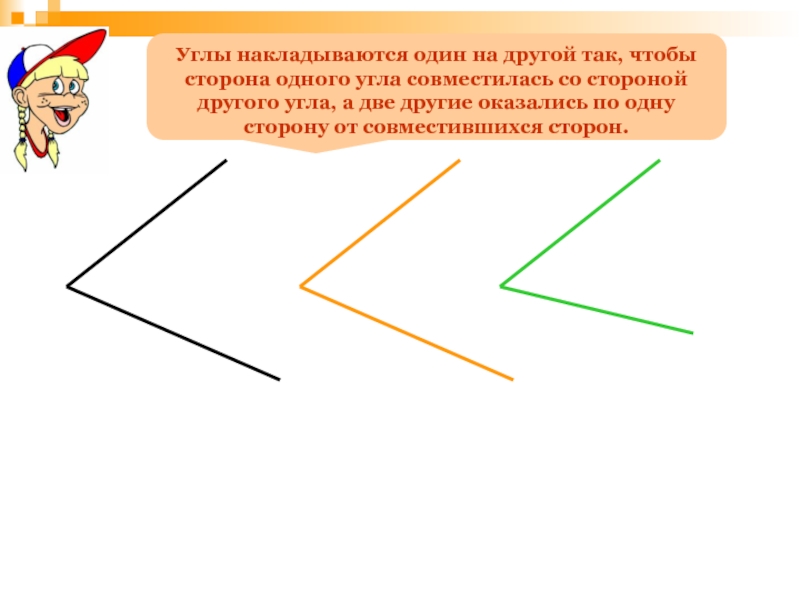
- 74. Углы накладываются один на другой так, чтобы
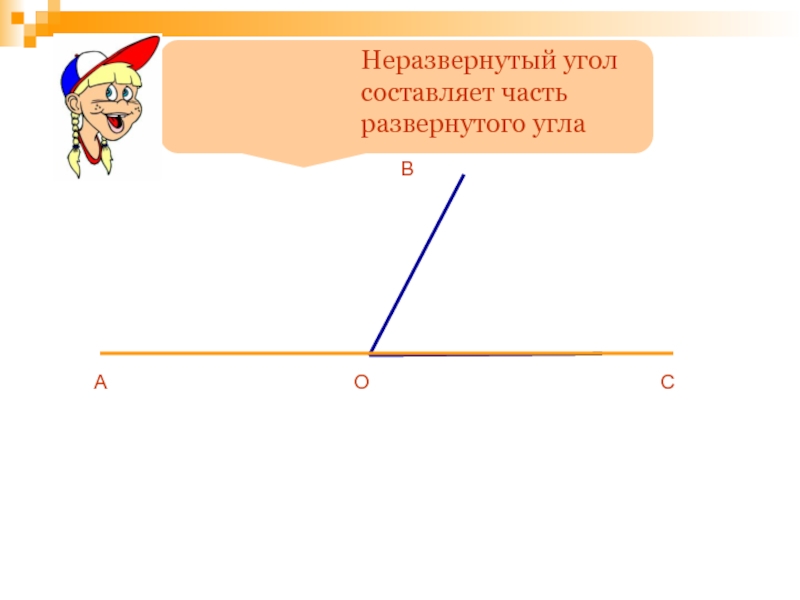
- 75. Неразвернутый угол составляет часть развернутого углаАОСВ
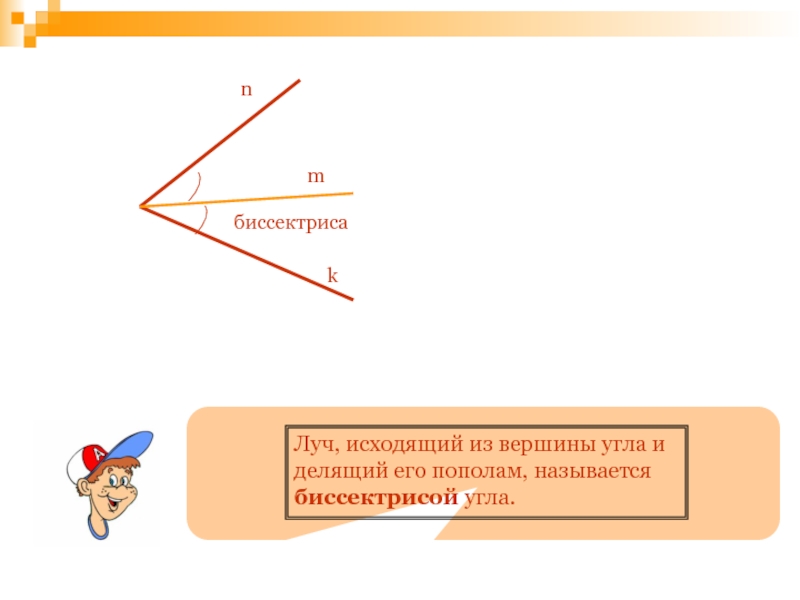
- 76. nmkбиссектрисаЛуч, исходящий из вершины угла и делящий его пополам, называется биссектрисой угла.
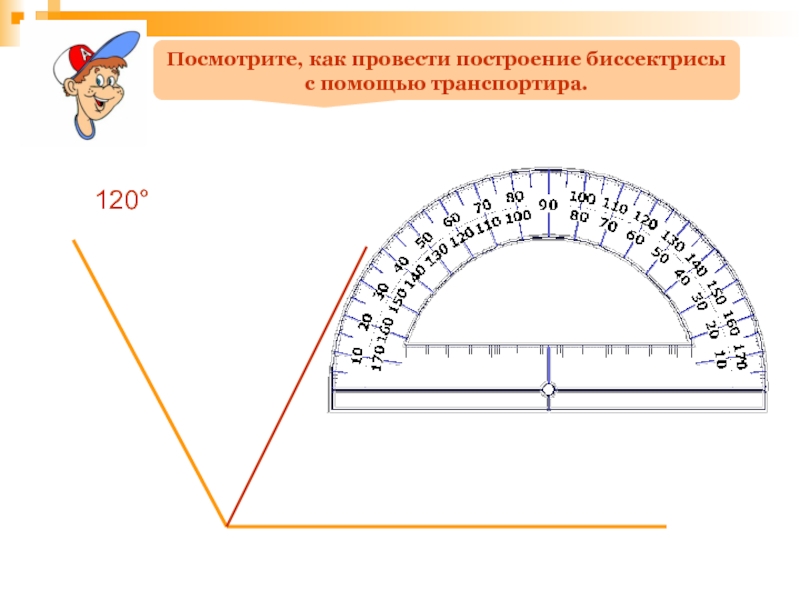
- 77. 120°Посмотрите, как провести построение биссектрисы с помощью транспортира.
- 78. №19№21№22Точка С – середина отрезка АВ, точка
- 79. Неразвернутый угол всегда равен развернутому.Биссектрисой угла называется
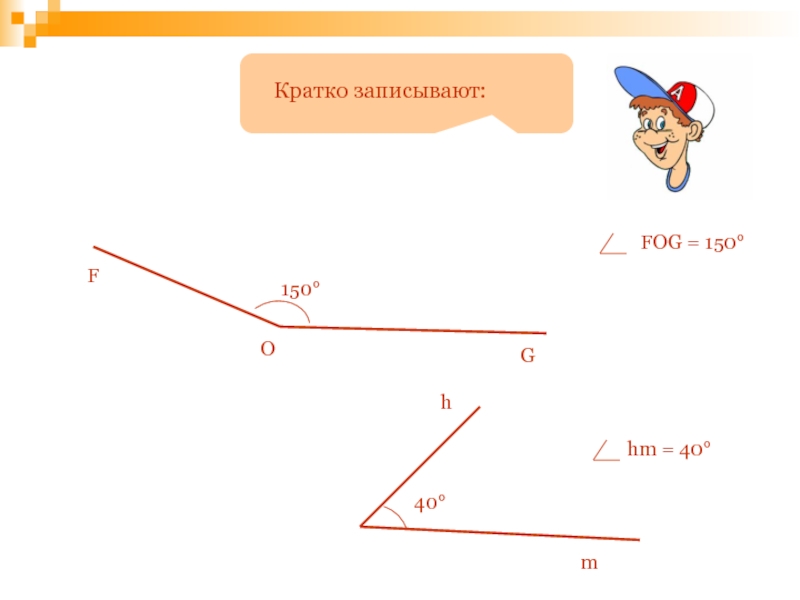
- 80. §3№18, 20, 23Запишите домашнее задание:
- 81. Урок 4 «Измерение отрезков»
- 82. Поверим домашнее задание:
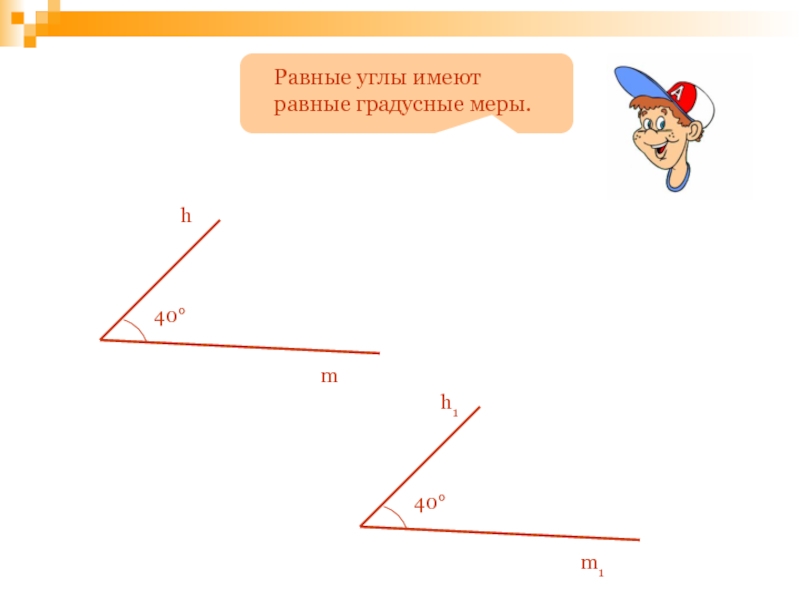
- 83. Проверка домашнего задания:№ 18ОВАСOB < OAOC > OAOB < OC
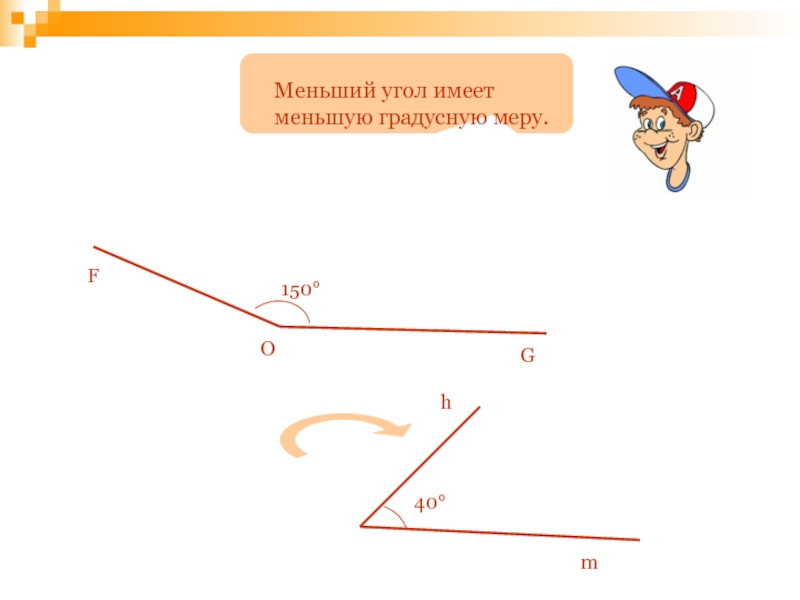
- 84. Проверка домашнего задания:№ 20В – середина АС, С – середина АЕ, D – середина СЕСЕBD, AE
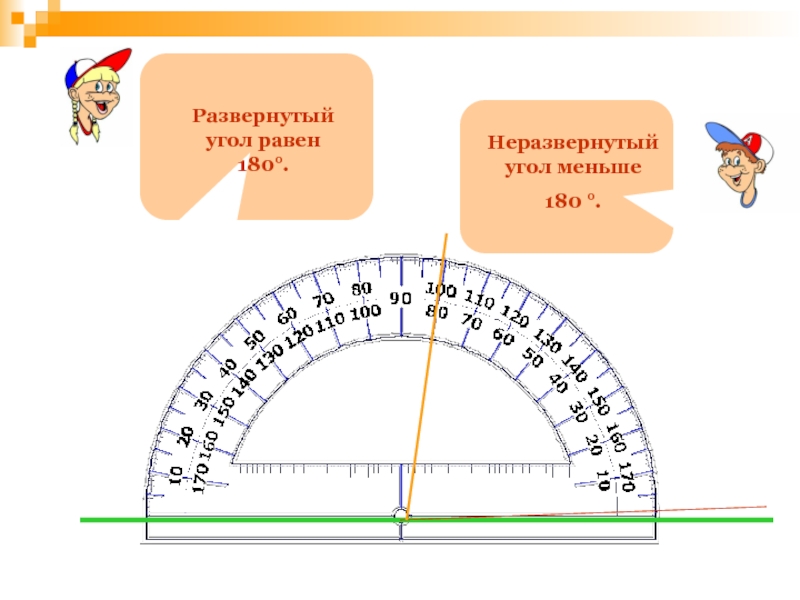
- 85. Проверка домашнего задания:№ 23ОВ – биссектриса угла
- 86. Подготовьте ответы на следующие вопросы:Какие фигуры называются
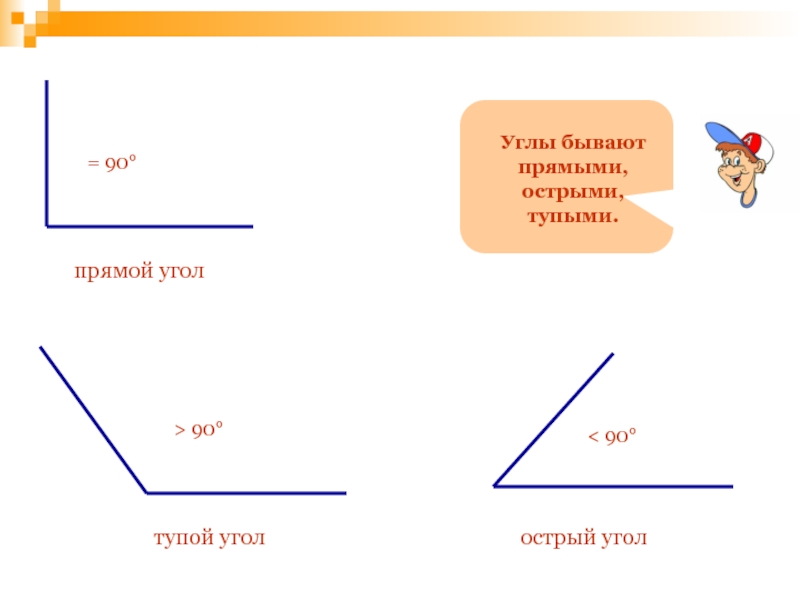
- 87. Исправьте ошибки, которые допустил Незнайка.Отрезки могут быть
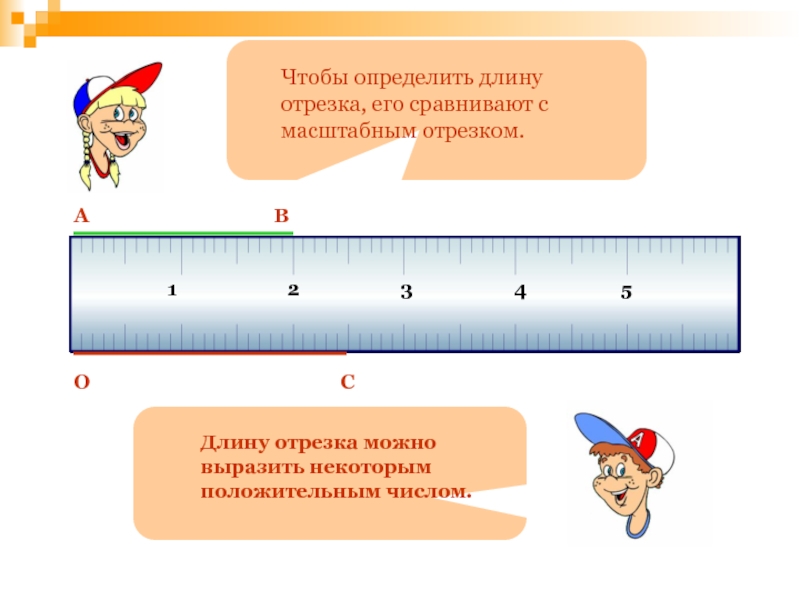
- 88. Чтобы определить длину отрезка, его сравнивают с масштабным отрезком.12345Длину отрезка можно выразить некоторым положительным числом.АВОС
- 89. Винни-Пух прочитал: «Расстояние от точки А до
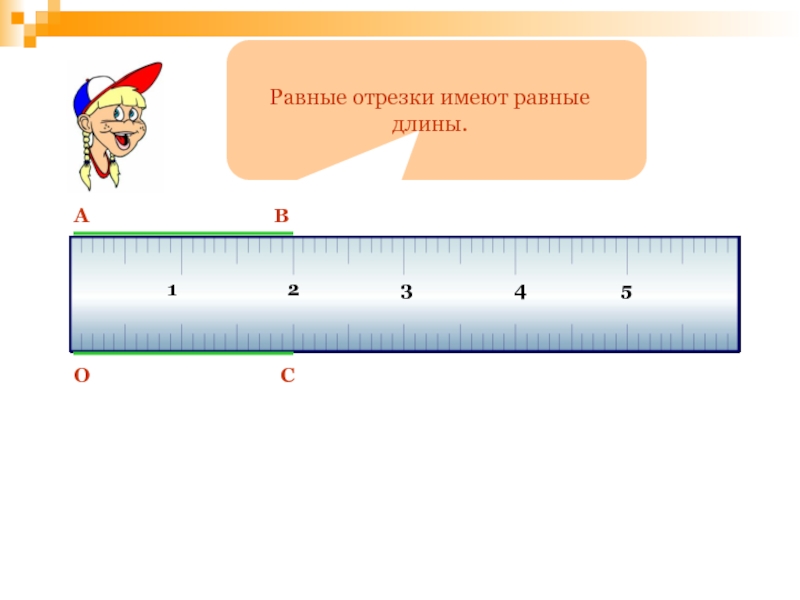
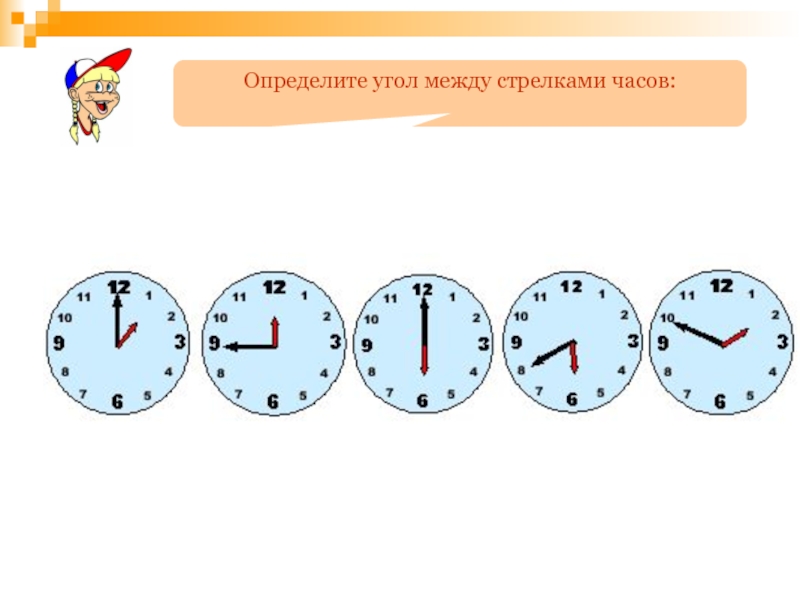
- 90. Равные отрезки имеют равные длины.12345АВОС
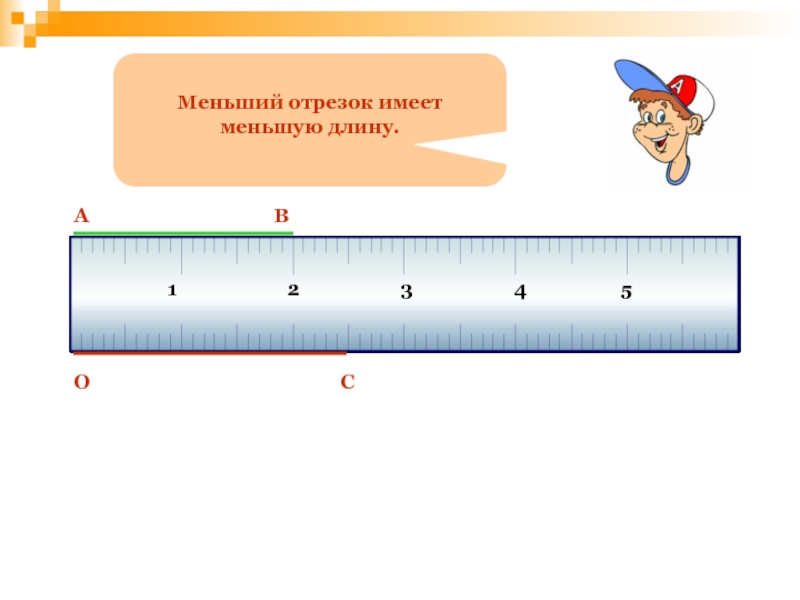
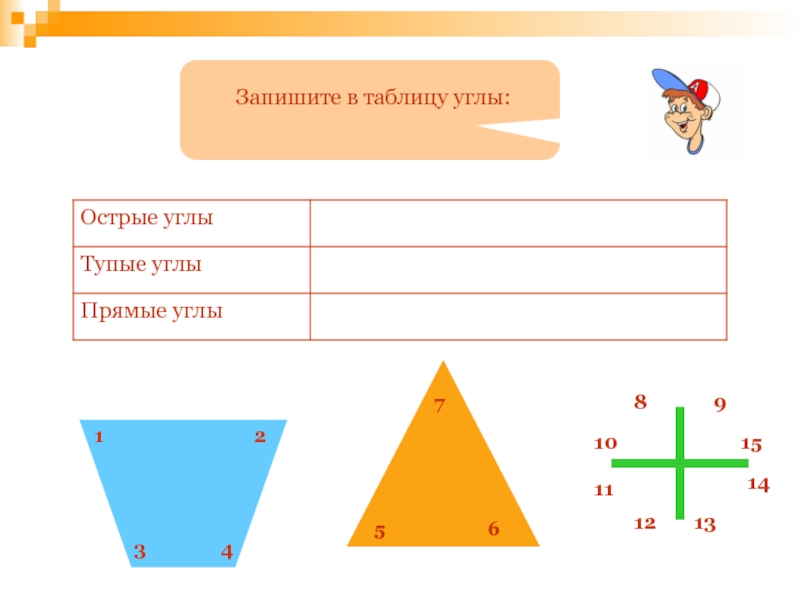
- 91. Меньший отрезок имеет меньшую длину.АВОС
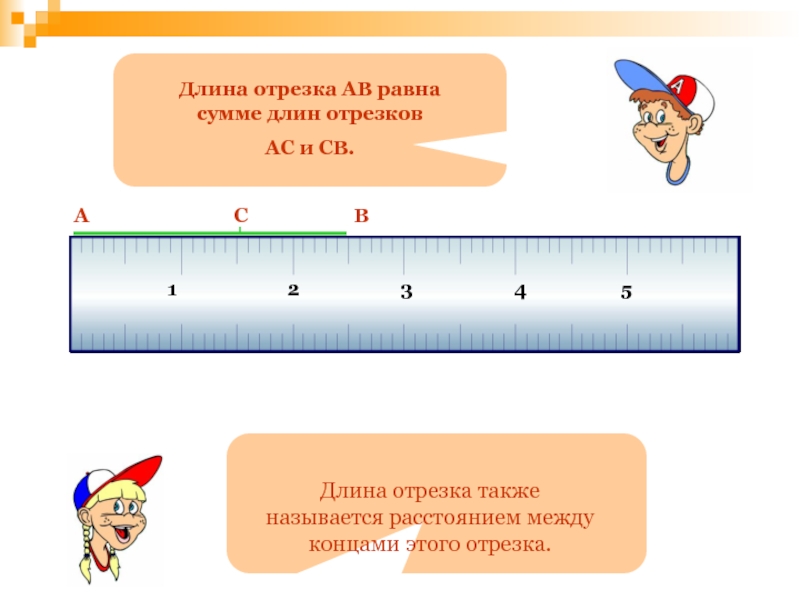
- 92. 12345Длина отрезка АВ равна сумме длин отрезков
- 93. Метр – стандартная международная единица измерения отрезков.эталон метраМетр ≈ 1/40 000 000 части земного меридиана.
- 94. Какие единицы измерения вы знаете?????
- 95. Инструменты, использующиеся на практике:линейка, в том числе масштабная миллиметроваяинструментырулетка
- 96. 1 м Пила имеет длину 1 метр,
- 97. №26273031 бРеши в тетради следующие задачи:
- 98. §4№ 24, 28, 29, 32Запишите домашнее задание:
- 99. Урок 5 «Измерение отрезков»
- 100. Поверим домашнее задание:
- 101. Проверка домашнего задания:№ 32ABC12 см13,5 смАС =
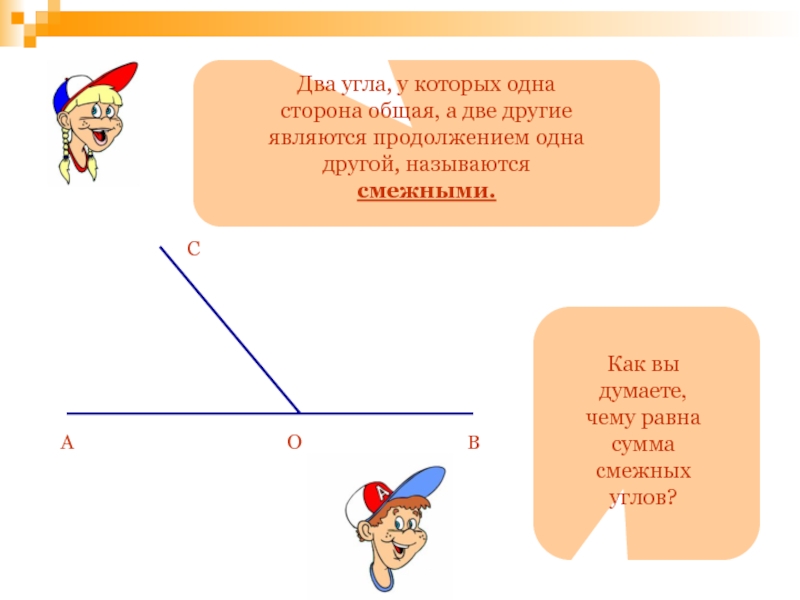
- 102. Подготовьте ответы на следующие вопросы:Что называют масштабным
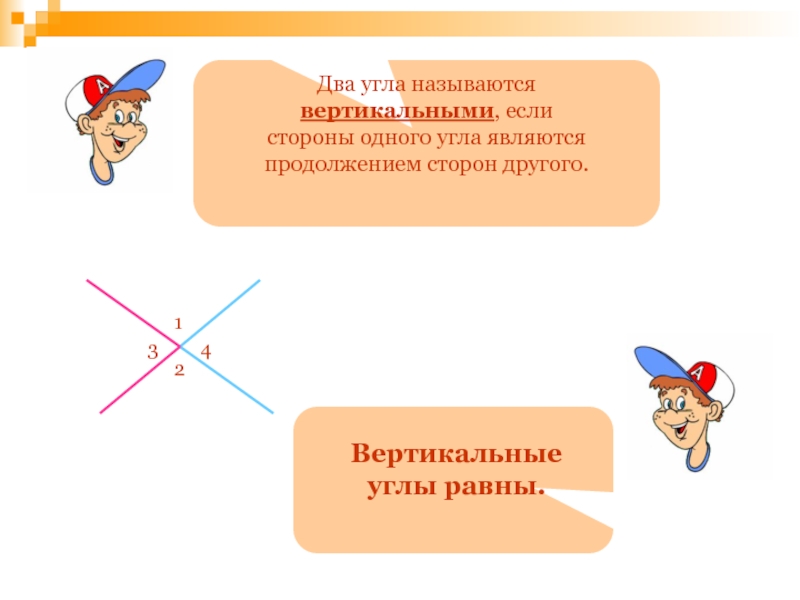
- 103. Из предложенных терминов выберите два, которые наиболее точно определяют математическое понятие «угол».
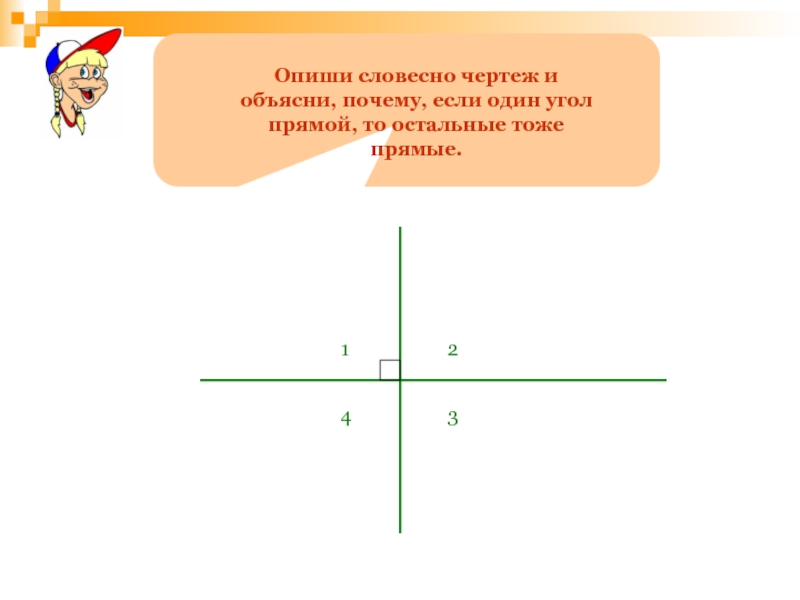
- 104. Определи закономерность и назови номера рисунков, в порядке соответствующей этой закономерности.
- 105. На прямой отмечены точки А, В, С,
- 106. Выполните самостоятельную работу в тетрадях.1 вариантНа прямой
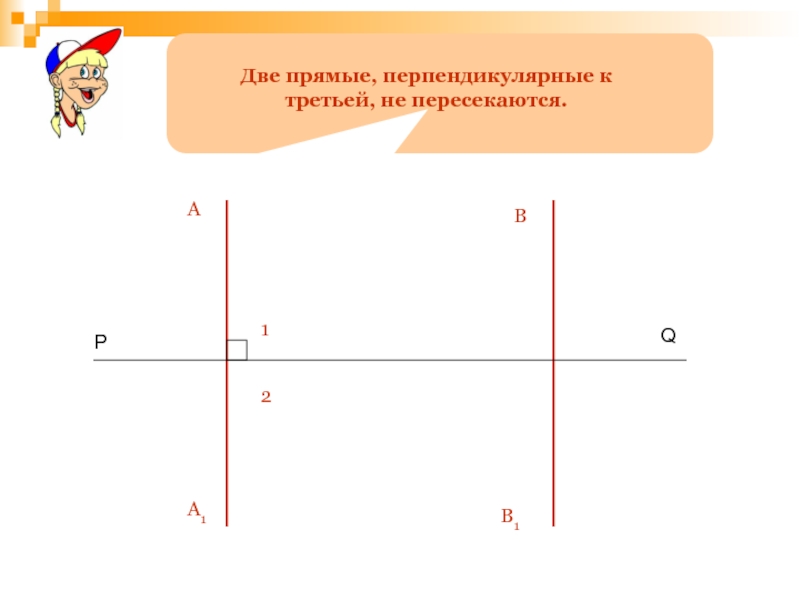
- 107. §4№ 31 а, 33, 37Запишите домашнее задание:
- 108. Урок 6 «Измерение углов»
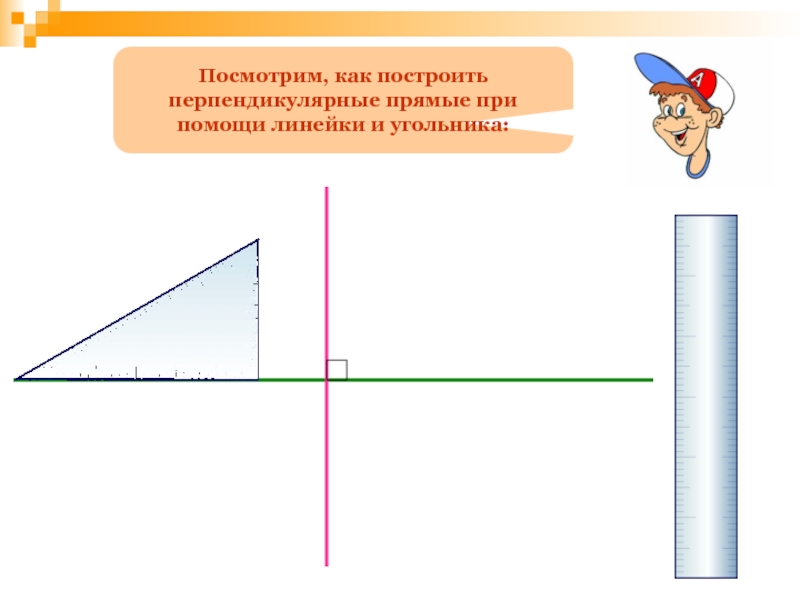
- 109. Поверим домашнее задание:
- 110. Проверка домашнего задания:№ 31 аАВС3,7 см7,2 смВС
- 111. Проверка домашнего задания:№ 33ВDM7 см16 смВM =
- 112. Проверка домашнего задания:№ 37АВСOAB = 2 cм,
- 113. Отгадайте шараду: первая часть слова – природное явление, вторая часть слова – есть у кошки.Подсказка:Ответ:градус
- 114. Единица измерения углов – градус.Градус – это
- 115. Для измерения углов используется транспортир.ТРАНСПОРТИР Он велик
- 116. Кратко записывают:150°40°hmFOGFOG = 150°hm = 40°
- 117. 1/60 часть градуса называется минутой. Обозначается: «´».1/60
- 118. Птолемей разделил окружность на 360° (градусов), каждую
- 119. Равные углы имеют равные градусные меры.40°h1m140°hm
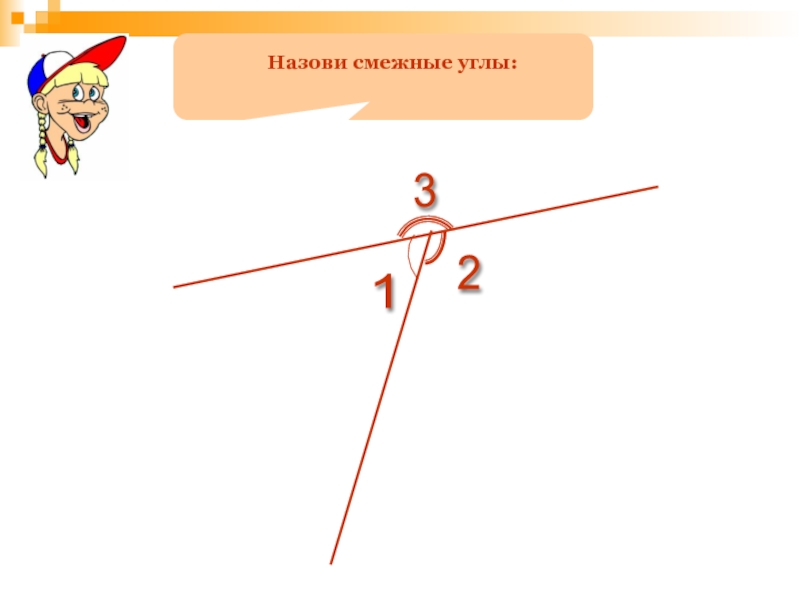
- 120. Меньший угол имеет меньшую градусную меру.150°40°hmFOG
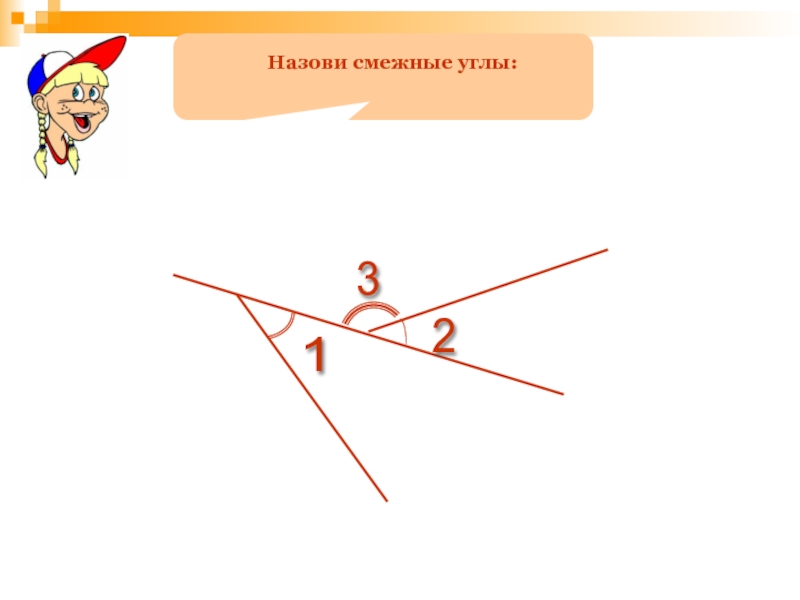
- 121. Развернутый угол равен 180°.Неразвернутый угол меньше 180 °.
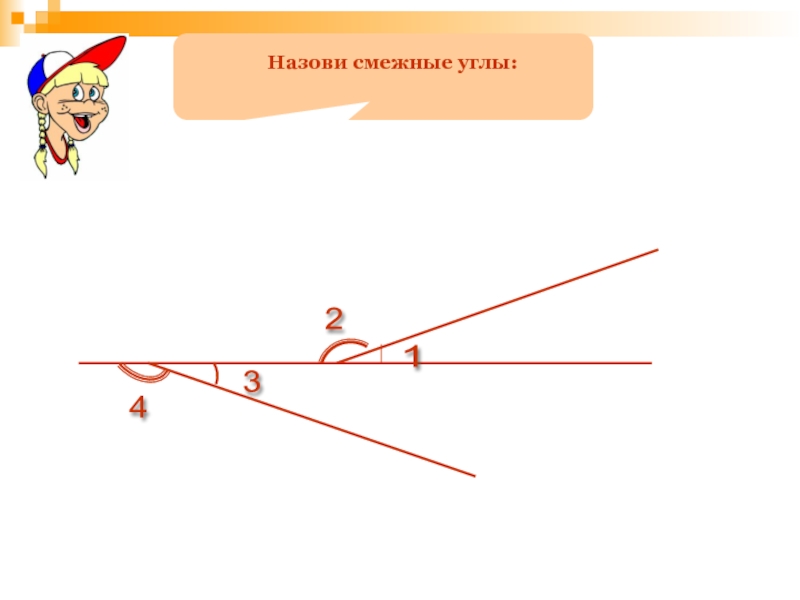
- 122. Если луч делит угол на два угла,
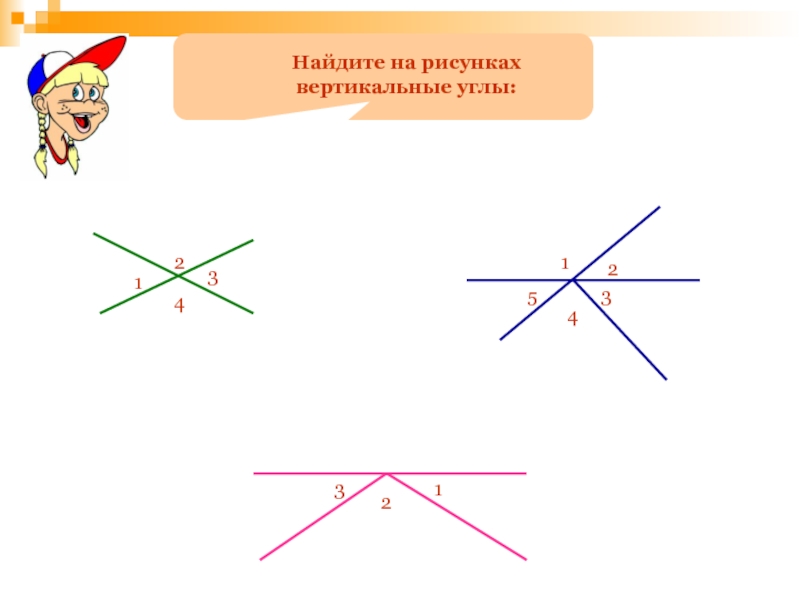
- 123. Углы бывают прямыми, острыми, тупыми.прямой уголтупой уголострый угол= 90°> 90°< 90°
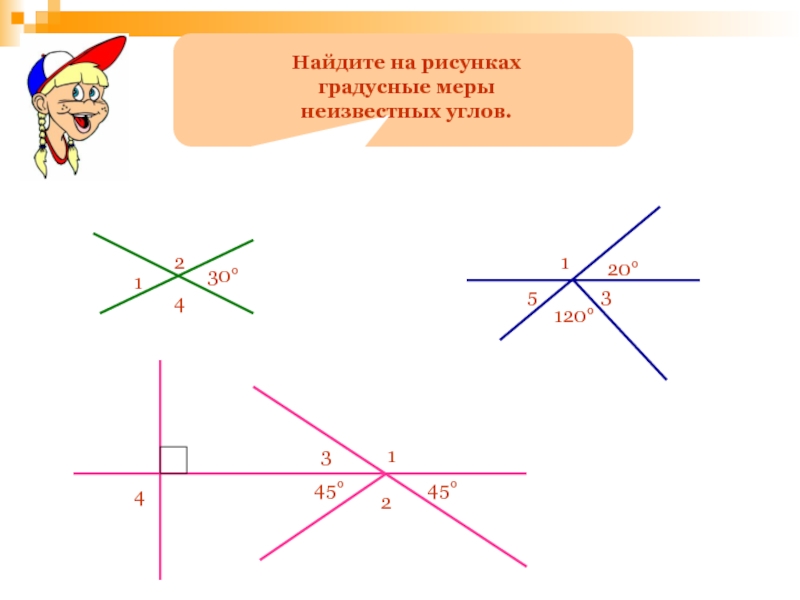
- 124. Измерение углов на местности проводят с помощью астролябии.
- 125. - Хотел бы проходить между твоими сторонами.
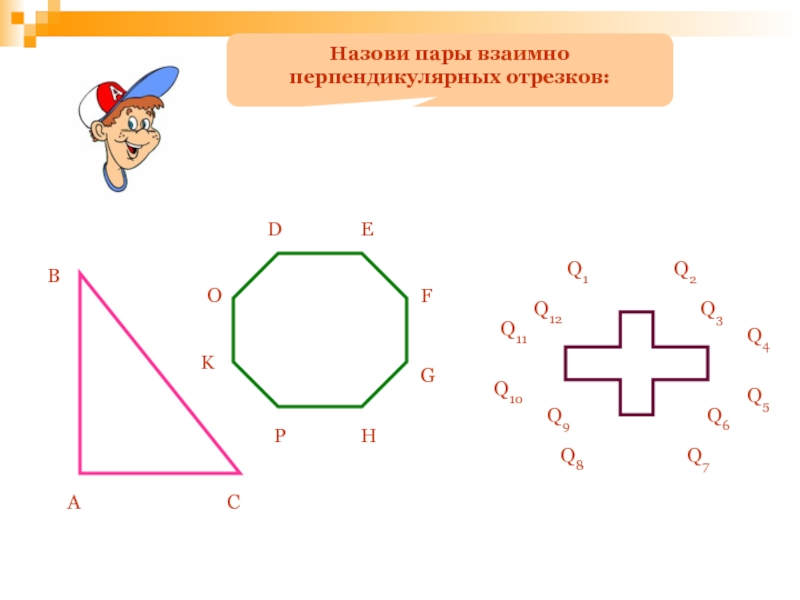
- 126. Определите угол между стрелками часов:
- 127. Запишите в таблицу углы:123456789101112131415
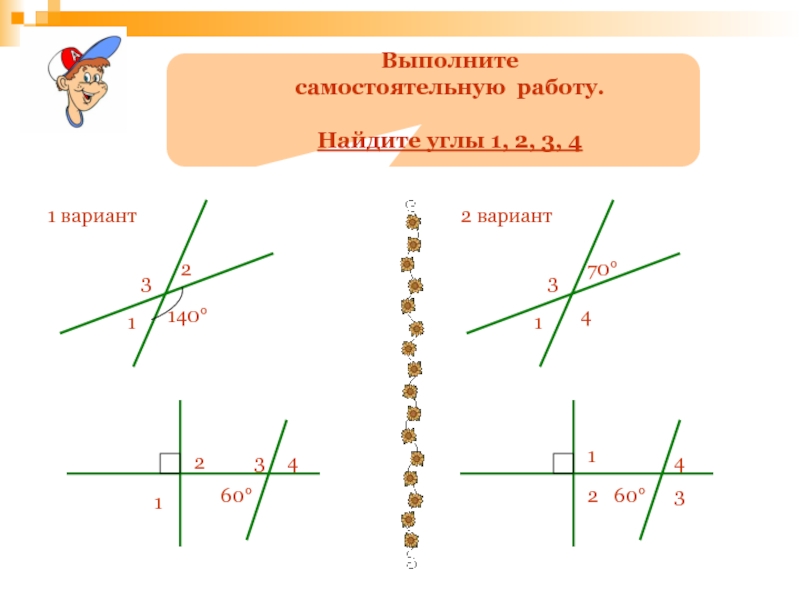
- 128. 120° – 32° = 38,5 °+ 85°
- 129. Выполните в тетрадях практическую работу:Начертите тупой угол
- 130. Реши в тетради следующие задачи:№ 45№ 46№ 53
- 131. §5№ 49, 50, 52Запишите домашнее задание:
- 132. Урок 7 «Перпендикулярные прямые»
- 133. Поверим домашнее задание:
- 134. Подготовьте ответы на следующие вопросы:Что принимают за
- 135. Проверка домашнего задания:№ 49ОСАВ?155°Решение:Пусть угол АОС =
- 136. Проверка домашнего задания:№ 50ОСАВ?108°Решение:Пусть угол СОВ =
- 137. Проверка домашнего задания:№ 52Решение:Угол XOZ = угол
- 138. Два угла, у которых одна сторона общая,
- 139. Два угла называются вертикальными, если стороны одного угла являются продолжением сторон другого.1234Вертикальные углы равны.
- 140. Опиши словесно чертеж и объясни, почему, если один угол прямой, то остальные тоже прямые.1234
- 141. Две прямые называются перпендикулярными, если они образуют
- 142. Перпендикуляр – от латинского слова “perpendicularis” («отвесный»)(Дело
- 143. Две прямые, перпендикулярные к третьей, не пересекаются.PQAA1В1В12
- 144. Есть ли на дереве ветви, перпендикулярные стволу?
- 145. Посмотрим, как построить перпендикулярные прямые при помощи линейки и угольника:
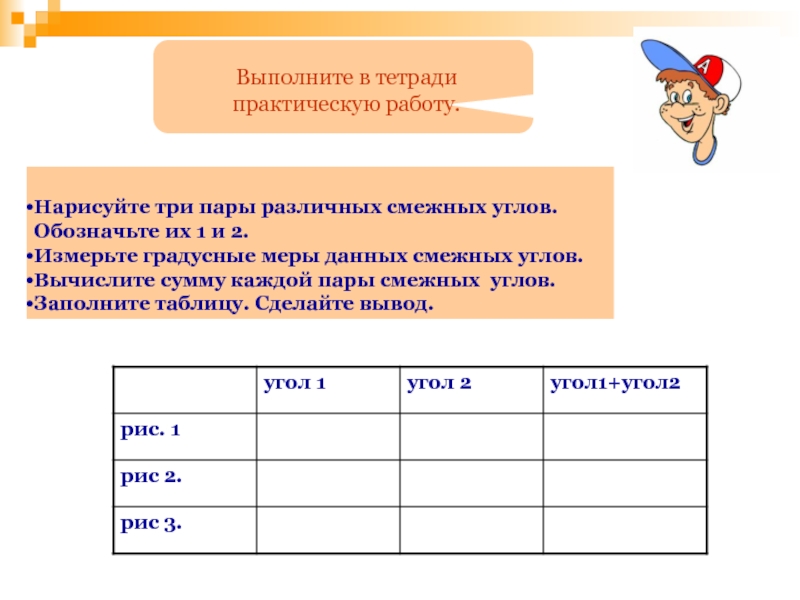
- 146. Нарисуйте три пары различных смежных углов. Обозначьте
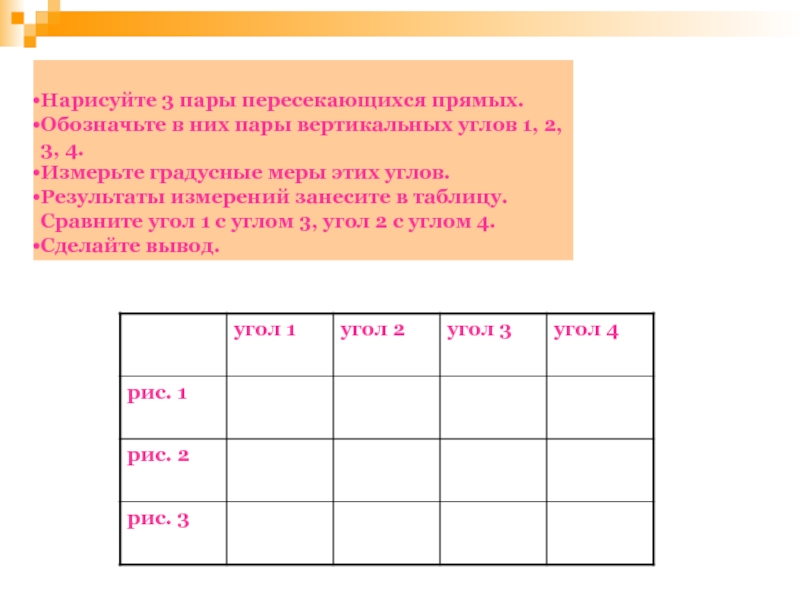
- 147. Нарисуйте 3 пары пересекающихся прямых. Обозначьте в
- 148. Даны смежные углы и три утверждения о
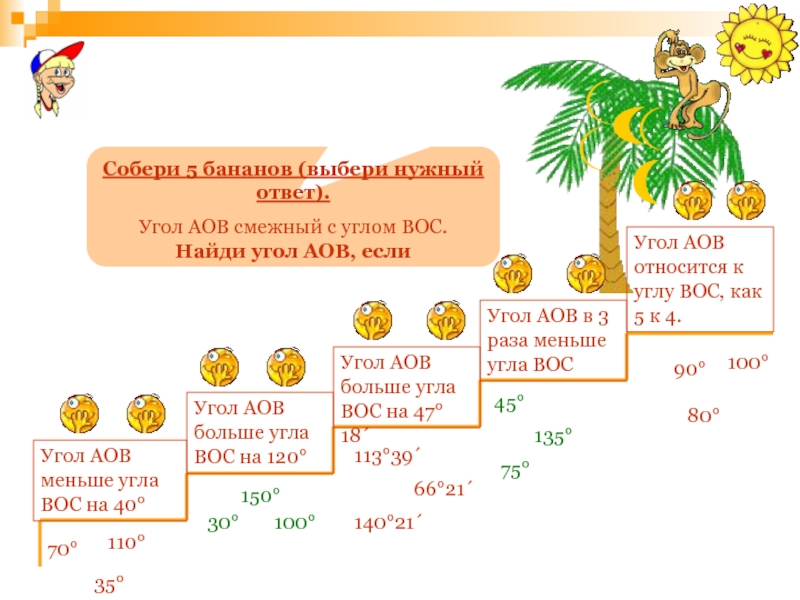
- 149. Собери 5 бананов (выбери нужный ответ).Угол АОВ
- 150. §6№ 57, 67, 68Запишите домашнее задание:Проверь себя, выполнив тест.
- 151. Урок 8 «Перпендикулярные прямые»
- 152. Поверим домашнее задание:
- 153. Подготовьте ответы на следующие вопросы:Какие углы называются
- 154. Проверка домашнего задания:№ 67Решение:3214Угол 3 и угол
- 155. № 68Проверка домашнего задания:OABCDEF50°70°Решение:Угол ВОС = углу
- 156. 1 2 3 Назови смежные углы:
- 157. 3 2 1 Назови смежные углы:
- 158. 1 2 3 4 Назови смежные углы:
- 159. Найдите на рисунках вертикальные углы:123412534123
- 160. Найдите на рисунках градусные меры неизвестных углов.1230°4120°53120°245°45°134
- 161. Ответьте на следующие вопросы:Один из смежных углов
- 162. Назови пары взаимно перпендикулярных отрезков:АBCDEFGHPKOQ1Q2Q3Q4Q5Q6Q7Q8Q9Q10Q11Q12
- 163. Построй перпендикулярные прямые, проходящие через точку М, к прямым a, b, c.
- 164. Выполните самостоятельную работу. Найдите углы 1, 2, 3, 4213140°60°12341370°460°12341 вариант2 вариант
- 165. Повторить всю теорию.№ 55, 64, 65 бЗапишите домашнее задание:Проверь себя, выполнив тест.
Урок 1 «Прямая и отрезок».Урок 2 «Луч и угол».Урок 3 «Сравнение отрезков и углов».Урок 4 «Измерение отрезков».Урок 5 «Измерение отрезков».Урок 6 «Измерение углов».Урок 7 «Перпендикулярные прямые».Урок 8 «Перпендикулярные прямые».
Слайд 2Урок 1 «Прямая и отрезок».
Урок 2 «Луч и угол».
Урок 3 «Сравнение
отрезков и углов».
Урок 4 «Измерение отрезков».
Урок 5 «Измерение отрезков».
Урок 6 «Измерение углов».
Урок 7 «Перпендикулярные прямые».
Урок 8 «Перпендикулярные прямые».
Урок 4 «Измерение отрезков».
Урок 5 «Измерение отрезков».
Урок 6 «Измерение углов».
Урок 7 «Перпендикулярные прямые».
Урок 8 «Перпендикулярные прямые».
Слайд 4
Ребята, прежде чем начать изучать геометрию, давайте узнаем, как зародилась эта
интереснейшая наука.
Слайд 5
Для первобытных людей важную роль играла форма окружавших предметов .
Добывая пищу,
возводя жилищные постройки, люди знакомились с простейшими геометрическими формами.
Уже 200 тысяч лет тому назад были изготовлены орудия труда сравнительно правильной геометрической формы.
Слайд 6
Пирамиды, которые были построены более 5 тыс. лет назад, состоят из
каменных блоков весом 15 тонн, подогнанных друг к другу так, что между ними невозможно протиснуть почтовую открытку.
Слайд 7
Издавна люди любили украшать свою одежду, дома.
В любом орнаменте прослеживаются геометрические
фигуры.
Слайд 8
Геометрия – “geо” – земля,
“metreo” – измерять.
Ребята, догадайтесь, какие геометрические
понятия возникли от данных слов:
«столик», «трапеза»
«льняная нить»
«ткнуть»
«бубен»
«спица колеса»?
«столик», «трапеза»
«льняная нить»
«ткнуть»
«бубен»
«спица колеса»?
Ответ:
трапеция, линия, точка, ромб, радиус.
Слайд 9
Первые геометрические понятия возникли из практических потребностей, например, они были связаны
с измерением земельных участков.
В египетских папирусах, вавилонских клинописных таблицах обнаружены образцы задач о вычислении площади.
В египетских папирусах, вавилонских клинописных таблицах обнаружены образцы задач о вычислении площади.
Слайд 10
В 3 веке до н.э. древнегреческий ученый Евклид написал книгу «Начала»,
которая позже стала энциклопедией геометрии.
Среди определений, написанных в этой книге, есть такие:
Точка есть то, что не имеет частей.
Линия есть длина без ширины.
Прямая есть такая линия, которая одинакова расположена по отношению ко всем своим точкам.
Среди определений, написанных в этой книге, есть такие:
Точка есть то, что не имеет частей.
Линия есть длина без ширины.
Прямая есть такая линия, которая одинакова расположена по отношению ко всем своим точкам.
Слайд 11
Величайшие геометры древности завершили создание античной геометрии.
Почти 2000 лет их труды
оставались непревзойденными.
Только после трудов замечательного русского математика Н.И. Лобачевского геометрия начинает развиваться дальше.
Только после трудов замечательного русского математика Н.И. Лобачевского геометрия начинает развиваться дальше.
Слайд 13
Геометрические понятия и определения задействованы во многих областях, например, в компьютерных
науках.
Слайд 14Векторная графика представляет изображение как набор примитивов. Обычно в качестве них
выбираются точки, прямые, окружности, прямоугольники.
Объектам присваиваются некоторые атрибуты, например, толщина линий, цвет заполнения.
Объектам присваиваются некоторые атрибуты, например, толщина линий, цвет заполнения.
Слайд 15Растровая графика – изображение состоит из точек (пикселов).
Каждому пикселю сопоставляется
значение — яркости, цвета, прозрачности — или комбинация этих значений.
Растровый образ имеет некоторое число строк и столбцов.
Растровый образ имеет некоторое число строк и столбцов.
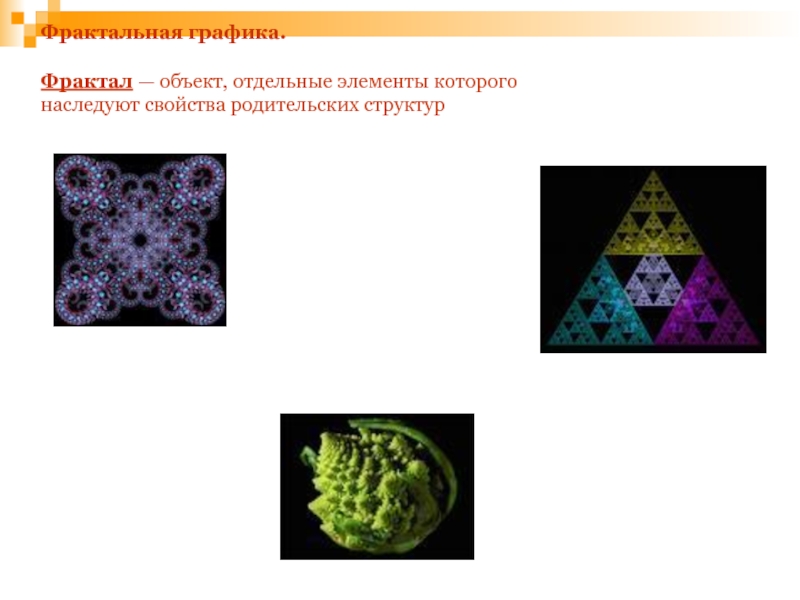
Слайд 16Фрактальная графика.
Фрактал — объект, отдельные элементы которого наследуют свойства родительских структур
Слайд 28Высота фигуры кажется большей чем, чем ее ширина, хотя в действительности
фигура имеет форму квадрата.
Слайд 30Прямая
Ломаная
Отрезок
Луч
Прямоугольник
Квадрат
Многоугольник
планиметрия
стереометрия
Какие геометрические фигуры вам известны?
Куб
Цилиндр
Шар
Конус
Пирамида
Параллелепипед
Слайд 31а
А
В
Прямую можно обозначить двумя способами:
маленькой латинской буквой,
двумя
большими латинскими буквами.
§ 1, стр. 5
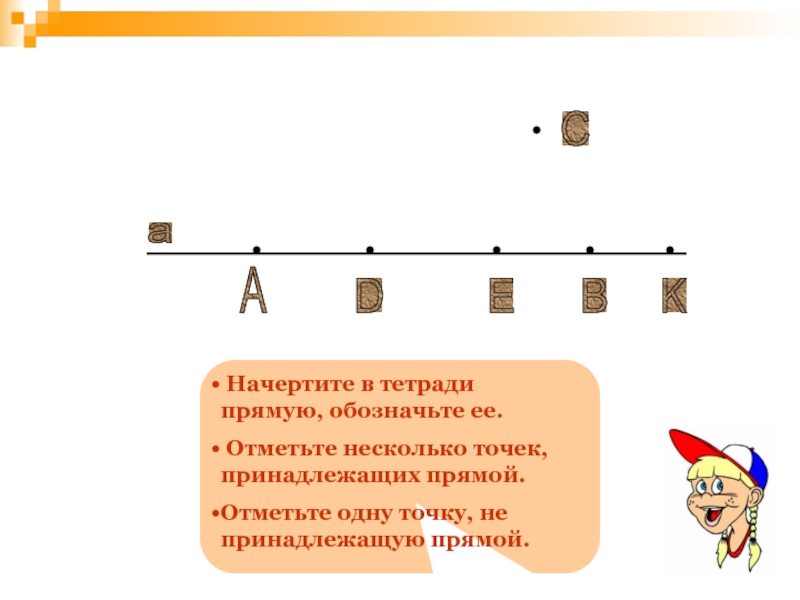
Слайд 32а
А
В
D
E
K
C
Начертите в тетради
прямую, обозначьте ее.
Отметьте несколько точек, принадлежащих прямой.
Отметьте одну точку, не принадлежащую прямой.
Отметьте несколько точек, принадлежащих прямой.
Отметьте одну точку, не принадлежащую прямой.
Слайд 33
«Точка D принадлежит прямой АВ, а точка С не принадлежит прямой
а»
В геометрии для краткой записи используют символы принадлежности:
є - принадлежит
є – не принадлежит
Слайд 34
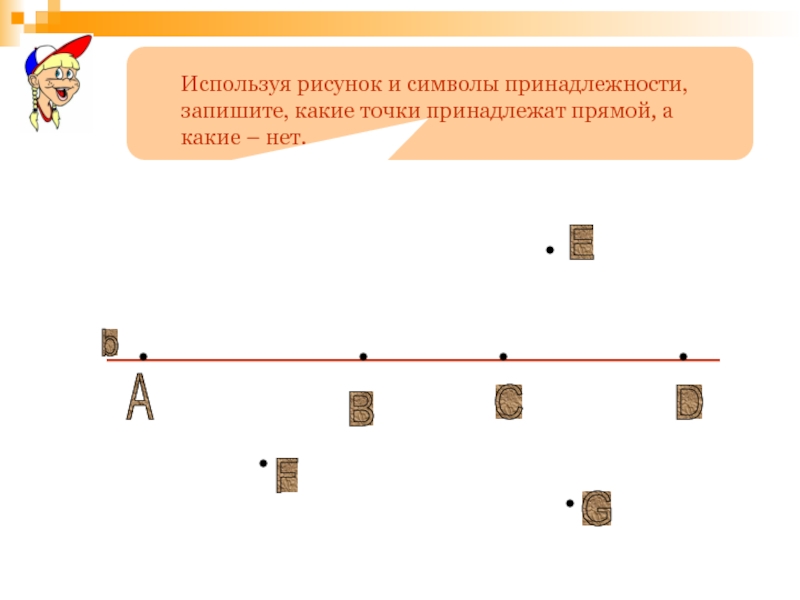
b
A
B
C
D
E
F
G
Используя рисунок и
символы принадлежности, запишите, какие точки принадлежат прямой, а какие – нет.
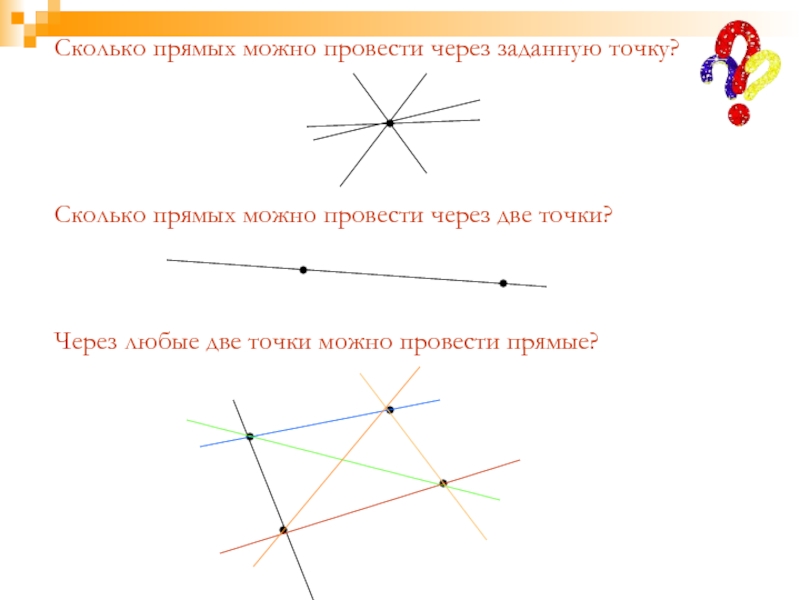
Слайд 35Сколько прямых можно провести через заданную точку?
Сколько прямых можно провести через
две точки?
Через любые две точки можно провести прямые?
Слайд 36
Свойство прямой.
Через любые две точки можно провести прямую и при том
только одну.
§ 1, стр. 5
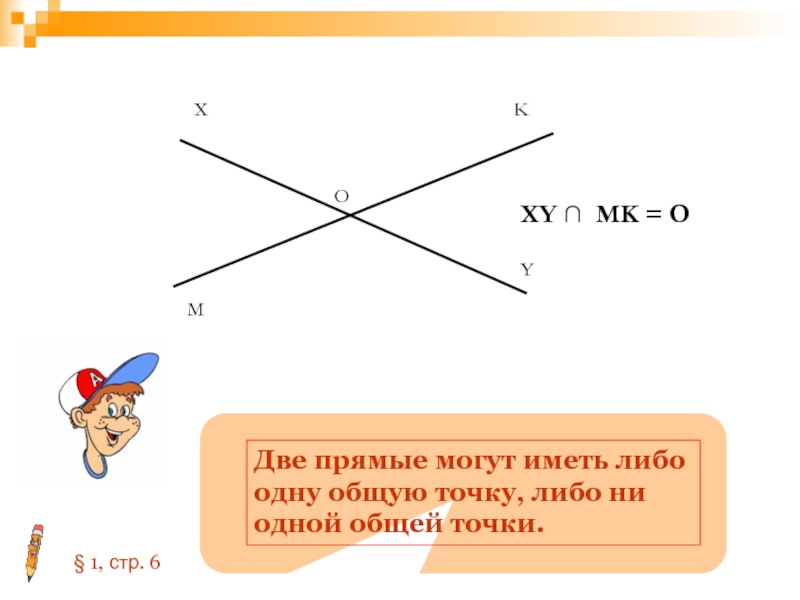
Слайд 37X
Y
M
K
O
XY ∩ MK = O
Две прямые могут иметь либо одну общую
точку, либо ни одной общей точки.
§ 1, стр. 6
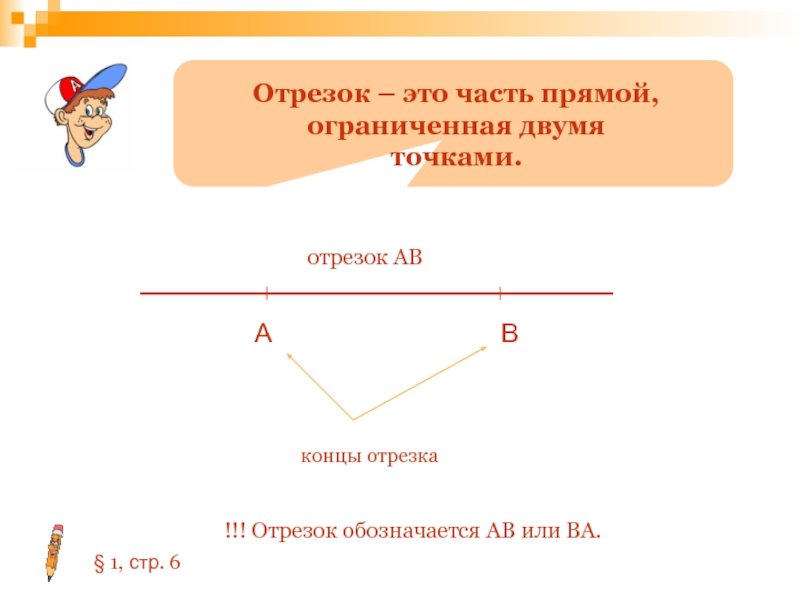
Слайд 38
Отрезок – это часть прямой, ограниченная двумя точками.
А
В
отрезок АВ
концы отрезка
!!! Отрезок
обозначается АВ или ВА.
§ 1, стр. 6
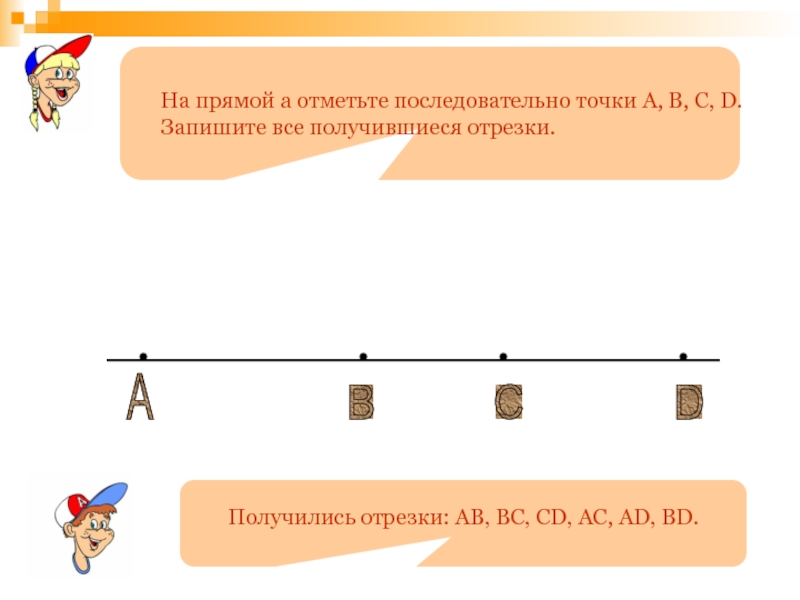
Слайд 39
A
B
C
D
На прямой а отметьте последовательно точки A,
B, C, D. Запишите все получившиеся отрезки.
Получились отрезки: AB, BC, CD, AC, AD, BD.
Слайд 41
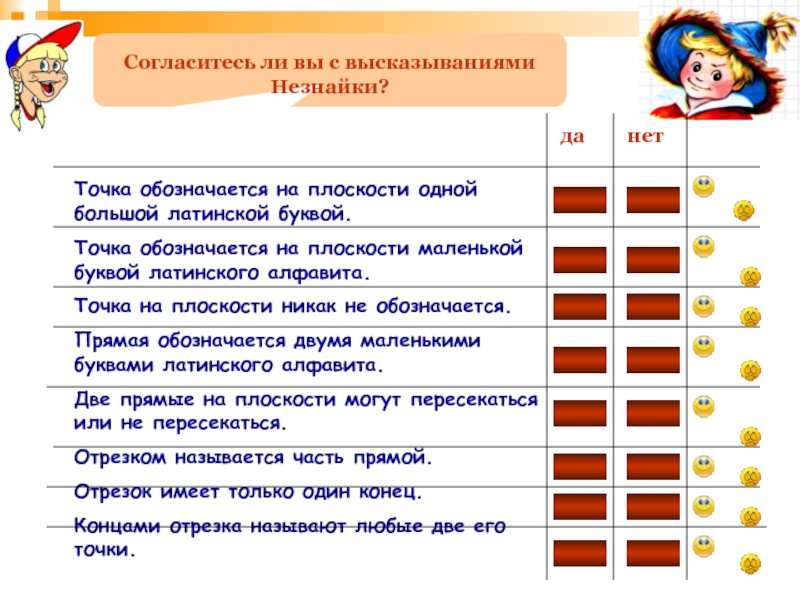
Точка обозначается на плоскости одной большой латинской буквой.
Точка обозначается на плоскости
маленькой буквой латинского алфавита.
Точка на плоскости никак не обозначается.
Прямая обозначается двумя маленькими буквами латинского алфавита.
Две прямые на плоскости могут пересекаться или не пересекаться.
Отрезком называется часть прямой.
Отрезок имеет только один конец.
Концами отрезка называют любые две его точки.
Точка на плоскости никак не обозначается.
Прямая обозначается двумя маленькими буквами латинского алфавита.
Две прямые на плоскости могут пересекаться или не пересекаться.
Отрезком называется часть прямой.
Отрезок имеет только один конец.
Концами отрезка называют любые две его точки.
да
нет
Согласитесь ли вы с высказываниями Незнайки?
Слайд 42
Мой друг изобразил прямую, кривую и ломаную линии. К сожалению, кто-то
испачкал его рисунок. Можно ли восстановить эти линии?
Слайд 43§ 1, 2, вопросы 1 – 3
№ 1, 3, 4, 7
Дополнительная
задача. Сколько различных прямых можно провести через четыре точки? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.
Запишите домашнее задание:
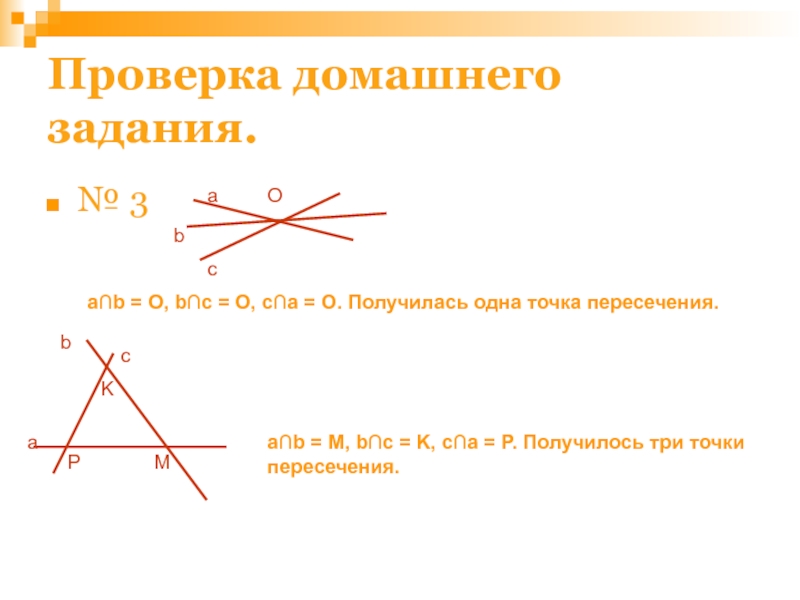
Слайд 46Проверка домашнего задания.
№ 3
О
a
b
c
a∩b = O, b∩c = O, c∩a =
O. Получилась одна точка пересечения.
c
b
a
P
M
K
a∩b = M, b∩c = K, c∩a = P. Получилось три точки
пересечения.
Слайд 49
Подготовьте ответы на следующие вопросы:
Что такое точка?
Как можно обозначить точку?
Что такое
прямая?
Как можно обозначить прямую?
Сколько прямых можно провести через две точки?
Сколько общих точек могут иметь две прямые?
Что называется отрезком?
Как обозначается отрезок?
Что называют концами отрезка?
Как называется прием построения прямой на местности?
Как можно обозначить прямую?
Сколько прямых можно провести через две точки?
Сколько общих точек могут иметь две прямые?
Что называется отрезком?
Как обозначается отрезок?
Что называют концами отрезка?
Как называется прием построения прямой на местности?
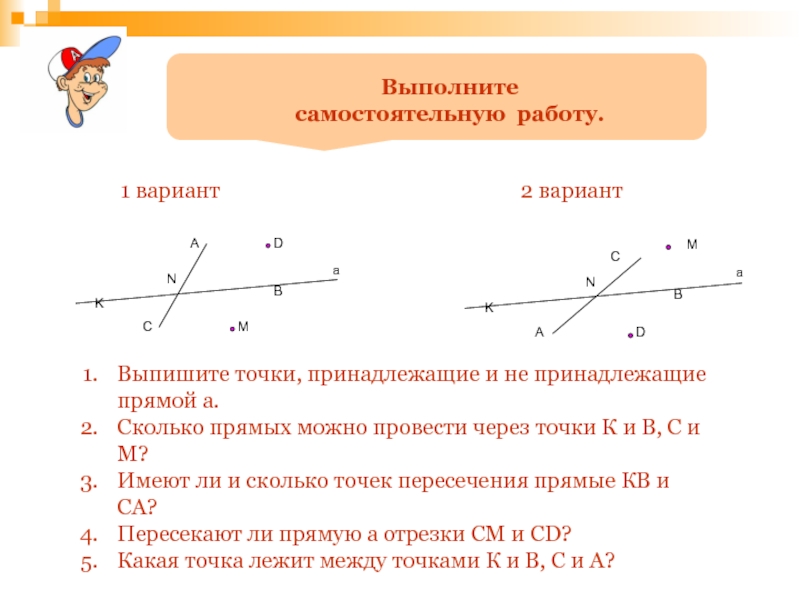
Слайд 50
Выполните
самостоятельную работу.
1 вариант
2 вариант
Выпишите точки, принадлежащие и не принадлежащие прямой
а.
Сколько прямых можно провести через точки К и В, С и М?
Имеют ли и сколько точек пересечения прямые КВ и СА?
Пересекают ли прямую а отрезки СМ и СD?
Какая точка лежит между точками К и В, С и А?
Сколько прямых можно провести через точки К и В, С и М?
Имеют ли и сколько точек пересечения прямые КВ и СА?
Пересекают ли прямую а отрезки СМ и СD?
Какая точка лежит между точками К и В, С и А?
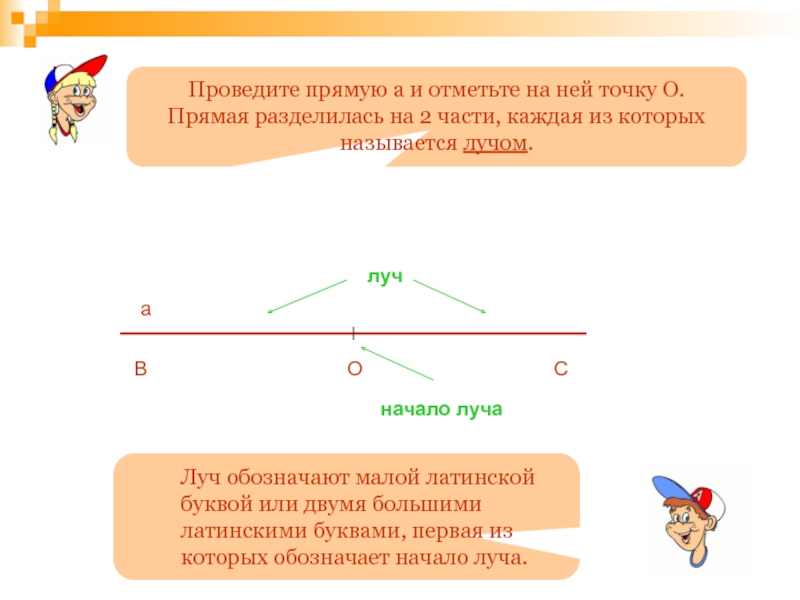
Слайд 51О
В
а
луч
начало луча
Проведите прямую а и отметьте на ней точку О.
Прямая разделилась
на 2 части, каждая из которых называется лучом.
С
Луч обозначают малой латинской буквой или двумя большими латинскими буквами, первая из которых обозначает начало луча.
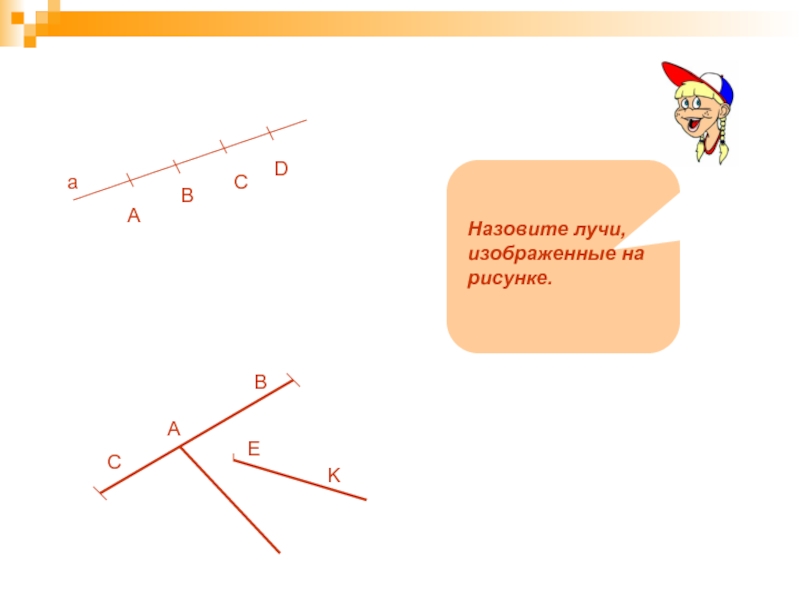
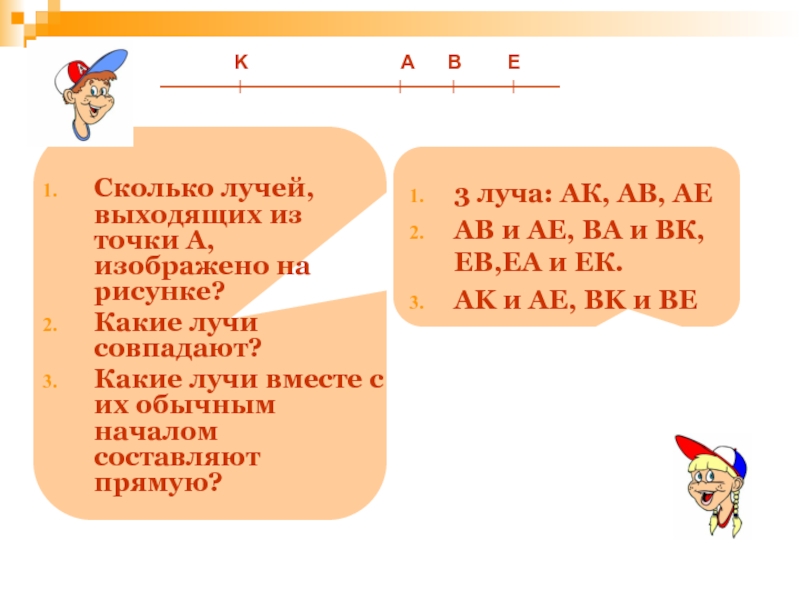
Слайд 53
A
K
B
E
Сколько лучей, выходящих из точки А, изображено на рисунке?
Какие лучи совпадают?
Какие
лучи вместе с их обычным началом составляют прямую?
3 луча: АК, АВ, АЕ
АВ и АЕ, ВА и ВК, ЕВ,ЕА и ЕК.
AK и AE, BK и BE
Слайд 54
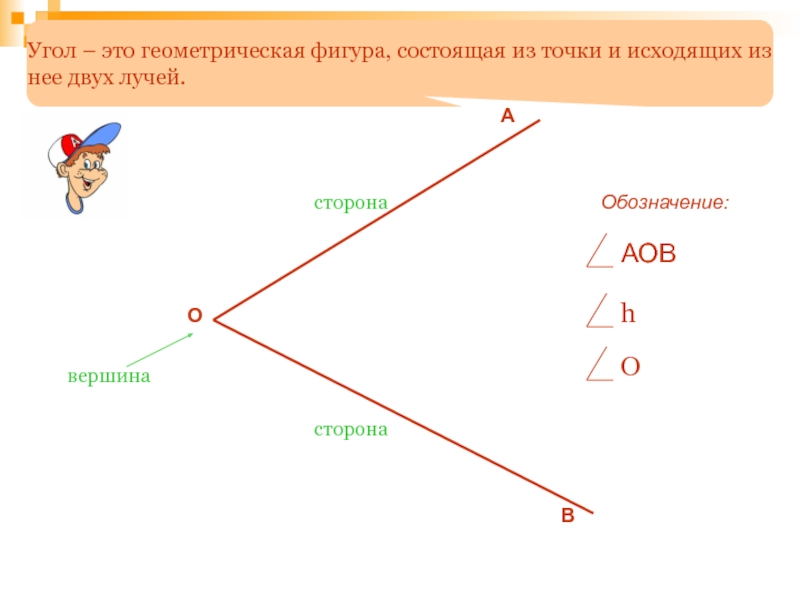
Угол – это геометрическая фигура, состоящая из точки и исходящих из
нее двух лучей.
вершина
сторона
сторона
АОВ
Обозначение:
h
О
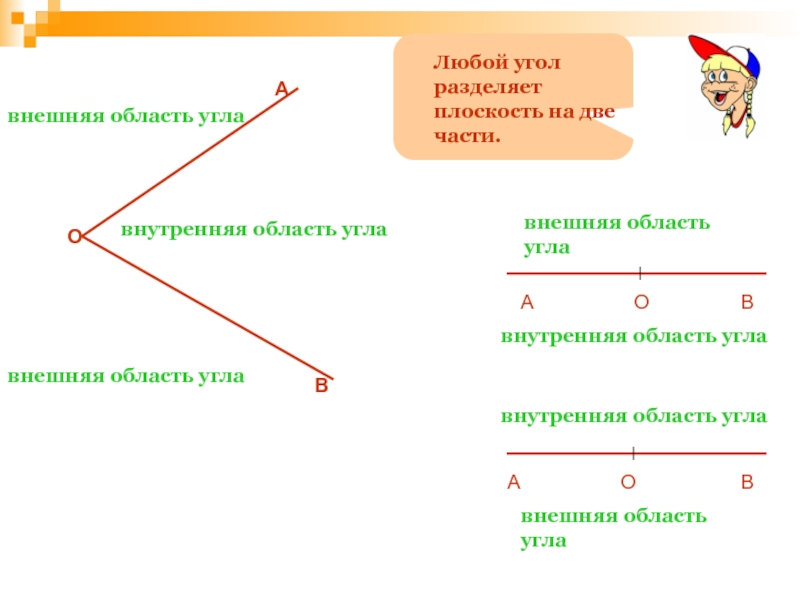
Слайд 55внутренняя область угла
внешняя область угла
внешняя область угла
А
О
В
А
О
В
внешняя область угла
внешняя область угла
внутренняя
область угла
внутренняя область угла
Любой угол разделяет плоскость на две части.
Слайд 56
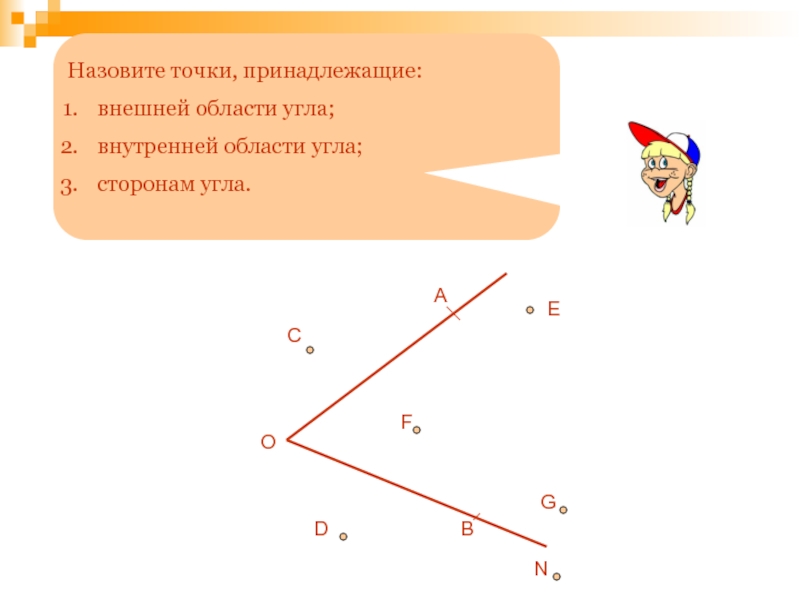
Назовите точки, принадлежащие:
внешней области угла;
внутренней области угла;
сторонам угла.
О
А
В
C
F
D
E
G
N
Слайд 58
Луч – это часть прямой, ограниченная одной точкой.
Начало луча всегда записывается
на втором месте.
Началом луча АВ является точка А.
Любой луч не имеет ни начала, ни конца.
При пересечении двух прямых получается четыре луча.
У любого угла может быть несколько вершин.
Угол можно обозначить тремя способами.
У любого угла может быть только две стороны.
Началом луча АВ является точка А.
Любой луч не имеет ни начала, ни конца.
При пересечении двух прямых получается четыре луча.
У любого угла может быть несколько вершин.
Угол можно обозначить тремя способами.
У любого угла может быть только две стороны.
да
нет
Согласитесь ли вы с высказываниями Незнайки?
Слайд 60
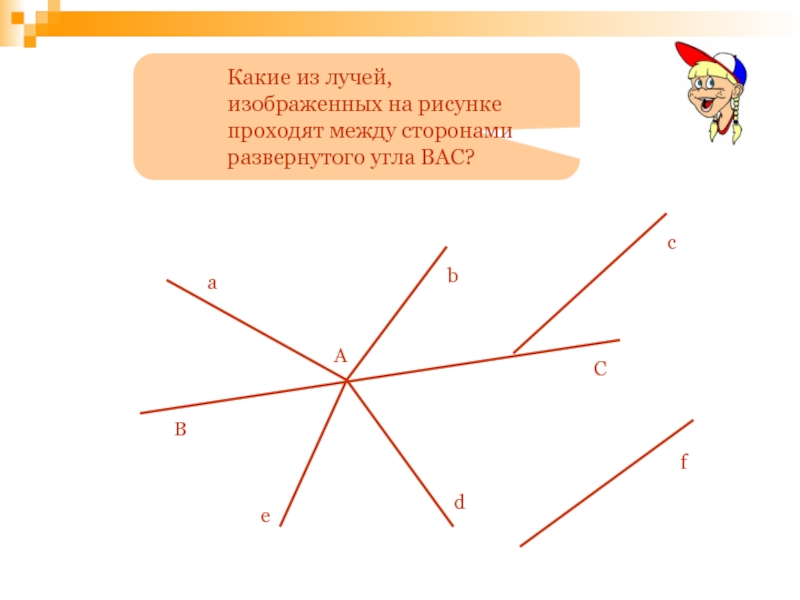
Какие из лучей, изображенных на рисунке проходят между сторонами развернутого угла
ВАС?
В
А
С
a
b
c
d
f
e
Слайд 61§2, вопросы 2-6
№11, 13, 14
Дополнительная задача. Сколько существует вариантов расположения трех
точек относительно угла?
Запишите домашнее задание:
Слайд 68
Подготовьте ответы на следующие вопросы:
Что называют лучом?
Как можно обозначить луч?
Что такое
угол?
Как можно обозначить угол?
Что называют сторонами угла?
Что такое вершина угла?
Какой угол называют развернутым?
На сколько частей угол разделяет плоскость? Как называют эти части?
Как можно обозначить угол?
Что называют сторонами угла?
Что такое вершина угла?
Какой угол называют развернутым?
На сколько частей угол разделяет плоскость? Как называют эти части?
Слайд 70
Сравни данные величины и сделай вывод.
отрезок АВ=20 см, отрезок CD =
2 дм;
угол АВС = 20°, угол MNK = 120°;
угол АВС = 20°, отрезок CD = 2 дм
угол АВС = 20°, угол MNK = 120°;
угол АВС = 20°, отрезок CD = 2 дм
Слайд 72Чтобы установить, равны ли отрезки, наложим один отрезок на другой так,
чтобы конец одного отрезка совместился с концом другого.
Слайд 74Углы накладываются один на другой так, чтобы сторона одного угла совместилась
со стороной другого угла, а две другие оказались по одну сторону от совместившихся сторон.
Слайд 76
n
m
k
биссектриса
Луч, исходящий из вершины угла и делящий его пополам, называется биссектрисой
угла.
Слайд 78№19
№21
№22
Точка С – середина отрезка АВ, точка О – середина отрезка
АС. Заполните таблицу:
Выполни самостоятельно работу
в тетради.
Слайд 79
Неразвернутый угол всегда равен развернутому.
Биссектрисой угла называется луч, делящий его на
два равных угла.
Любые два развернутых угла всегда равны.
Любые два развернутых угла не всегда равны.
Любые два развернутых угла всегда не равны.
Любые два неразвернутых угла могут быть равны.
Любые два неразвернутых угла всегда не равны.
Любой луч, исходящий из вершины угла, делит его пополам.
Любые два развернутых угла всегда равны.
Любые два развернутых угла не всегда равны.
Любые два развернутых угла всегда не равны.
Любые два неразвернутых угла могут быть равны.
Любые два неразвернутых угла всегда не равны.
Любой луч, исходящий из вершины угла, делит его пополам.
да
нет
Согласитесь ли вы с высказываниями Незнайки?
Слайд 85Проверка домашнего задания:
№ 23
ОВ – биссектриса угла АОВ, ОD – биссектриса
угла BOF, ОС – биссектриса угла АОЕ.
BOD, AOE
BOD, AOE
Слайд 86
Подготовьте ответы на следующие вопросы:
Какие фигуры называются равными?
Как сравнить отрезка?
Что называется
серединой отрезка?
Как сравнить углы?
Что называется биссектрисой угла?
Как сравнить углы?
Что называется биссектрисой угла?
Слайд 87
Исправьте ошибки, которые допустил Незнайка.
Отрезки могут быть измерены с помощью различных
приспособлений: градусника, часов, линейки, спидометра, циркуля, транспортиром, поэтому длина и ширина любого отрезка может быть измерена в разных единицах: в градусах, минутах и часах, сантиметрах, километрах в час, причем длина отрезка может быть как положительной, так и отрицательной величиной в зависимости от его направления.
Слайд 88
Чтобы определить длину отрезка, его сравнивают с масштабным отрезком.
1
2
3
4
5
Длину отрезка можно
выразить некоторым положительным числом.
А
В
О
С
Слайд 89Винни-Пух прочитал:
«Расстояние от точки А до точки В равно 5
см, а от точки В до точки С – 3 см».
Что означает знак «-» - тире или минус?"
Что означает знак «-» - тире или минус?"
Слайд 921
2
3
4
5
Длина отрезка АВ равна сумме длин отрезков
АС и СВ.
А
В
С
Длина отрезка
также называется расстоянием между концами этого отрезка.
Слайд 93
Метр – стандартная международная единица измерения отрезков.
эталон метра
Метр ≈ 1/40 000
000 части земного меридиана.
Слайд 95
Инструменты, использующиеся на практике:
линейка, в том числе масштабная миллиметровая
инструменты
рулетка
Слайд 961 м
Пила имеет длину 1 метр, расстояние между соседними зубцами
равна 25 мм. Найдите число зубцов пилы.
Слайд 101Проверка домашнего задания:
№ 32
A
B
C
12 см
13,5 см
АС = АВ + ВС =
12 +13,5 = 25,5 (см)
A
B
C
12 см
13,5 см
АС = ВС – АВ = 13,5 – 12 = 1,5 (см)
Слайд 102
Подготовьте ответы на следующие вопросы:
Что называют масштабным отрезком?
Каким числом выражается длина
отрезка?
На сколько частей разбивает отрезок точка, лежащая на этом отрезке?
Какие длины имеют равные отрезки?
Как еще называют длину отрезка?
Чему равна длина отрезка в случае, когда некоторая точка делит данный отрезок на два?
Чему приближенно равен метр?
Какие единицы измерения вы знаете?
Назовите инструменты, использующиеся на практике для измерения расстояний.
На сколько частей разбивает отрезок точка, лежащая на этом отрезке?
Какие длины имеют равные отрезки?
Как еще называют длину отрезка?
Чему равна длина отрезка в случае, когда некоторая точка делит данный отрезок на два?
Чему приближенно равен метр?
Какие единицы измерения вы знаете?
Назовите инструменты, использующиеся на практике для измерения расстояний.
Слайд 103
Из предложенных терминов выберите два, которые наиболее точно определяют математическое понятие
«угол».
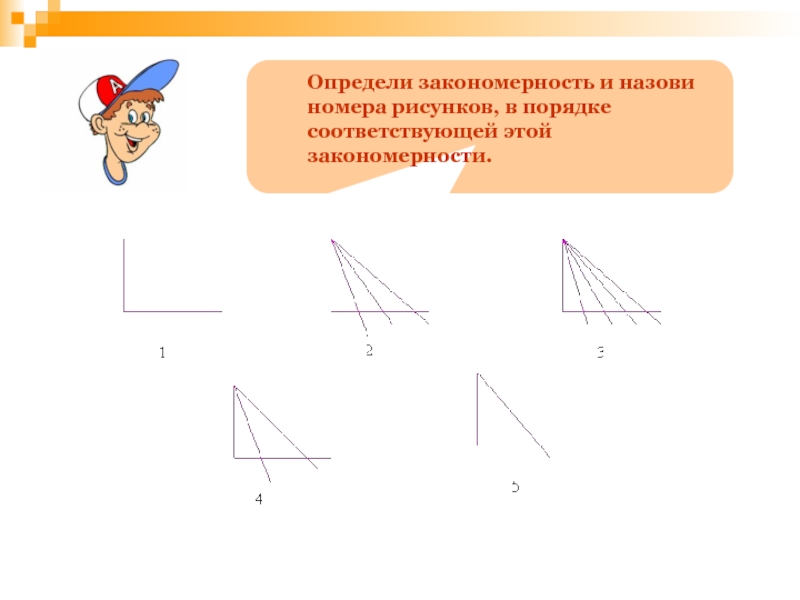
Слайд 104
Определи закономерность и назови номера рисунков, в порядке соответствующей этой закономерности.
Слайд 105На прямой отмечены точки А, В, С, D, Н так, что
АВ=ВС=СD=DН. Какие еще равные отрезки определяют эти точки?
Реши в тетради следующие задачи:
Точка D принадлежит отрезку АВ. Длина отрезка АВ = 75 см. Найди длины отрезков АD и ВD, если
а) АD = 1\4 ВD
б) АD = 2 ВD
в) АD : ВD = 3 : 2.
Слайд 106Выполните самостоятельную работу в тетрадях.
1 вариант
На прямой а отмечены точки C,
D, E так, что CD=6 см, DE=8 см. Какой может быть длина отрезка СЕ?
Точка М – середина отрезка АВ, МВ = 4,3 дм. Найдите длину отрезка АВ в миллиметрах.
Точка М – середина отрезка АВ, МВ = 4,3 дм. Найдите длину отрезка АВ в миллиметрах.
2 вариант
На прямой b отмечены точки А, В, С так, что АС=12 см, АВ = 8 см. Какой может быть длина отрезка ВС?
Точка Р – середина отрезка MN. Найдите длину отрезка PN в метрах, если MN = 14 дм.
Слайд 111Проверка домашнего задания:
№ 33
В
D
M
7 см
16 см
ВM = BD + DM =
7 + 16 = 23(см)
В
D
M
7 см
16 см
ВM = DM - BD = 16 - 7 = 9(см)
Слайд 112Проверка домашнего задания:
№ 37
А
В
С
O
AB = 2 cм, тогда АС = 1
см, СВ = 1 см, АО = 0,5 см, ОВ = 1,5 см
СВ = 3,2 см, тогда АВ = 6,4 см, АС = 3,2 см, АО = 1,6 см, ОВ = 4,8 см
СВ = 3,2 см, тогда АВ = 6,4 см, АС = 3,2 см, АО = 1,6 см, ОВ = 4,8 см
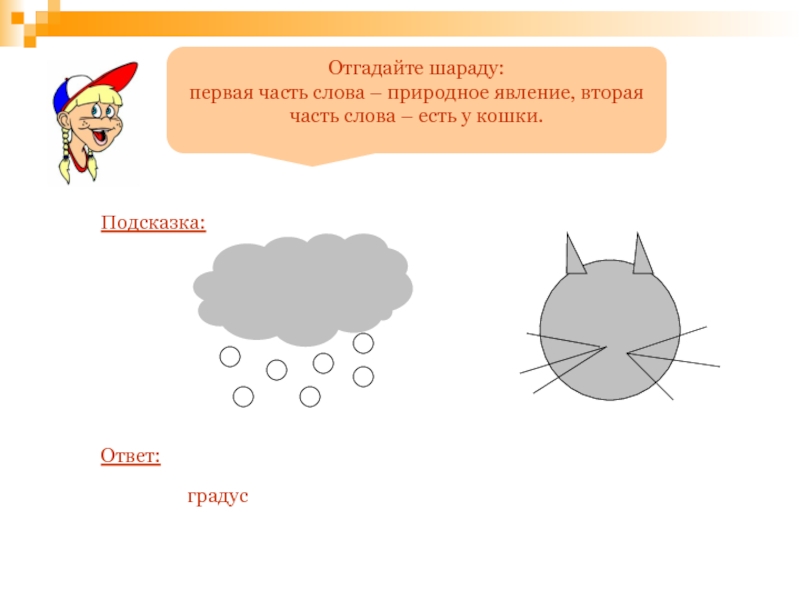
Слайд 113Отгадайте шараду:
первая часть слова – природное явление, вторая часть слова
– есть у кошки.
Подсказка:
Ответ:
градус
Слайд 114
Единица измерения углов – градус.
Градус – это угол, равный 1/180 части
развернутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла.
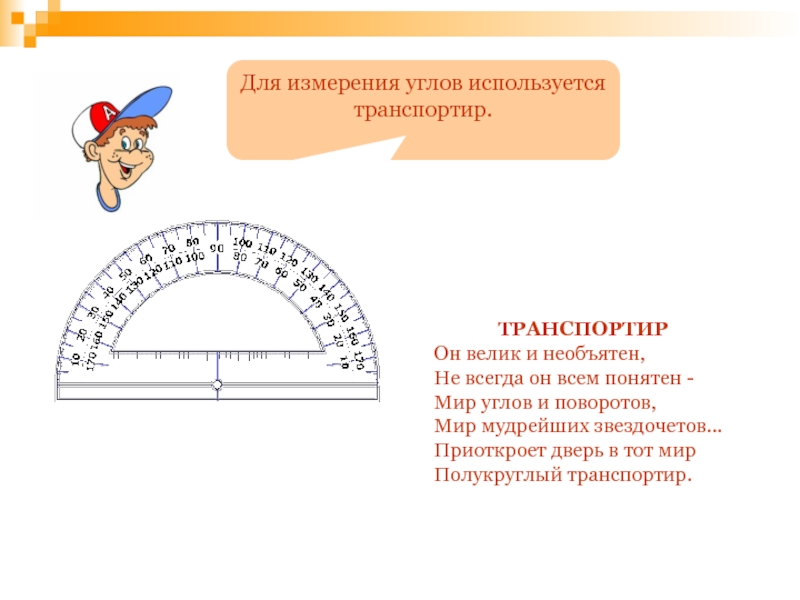
Слайд 115Для измерения углов используется транспортир.
ТРАНСПОРТИР
Он велик и необъятен,
Не всегда
он всем понятен - Мир углов и поворотов,
Мир мудрейших звездочетов... Приоткроет дверь в тот мир Полукруглый транспортир.
Мир мудрейших звездочетов... Приоткроет дверь в тот мир Полукруглый транспортир.
Слайд 117
1/60 часть градуса называется минутой. Обозначается: «´».
1/60 часть минуты называется секундой.
Обозначается: «″»
Угол в 60 градусов, 32 минуты, 45 секунд обозначается: 60°32′45″
Слайд 118
Птолемей разделил окружность на 360° (градусов), каждую часть на 60 «первых
мелких долей», а каждую «первую мелкую» долю на 60 «вторых мелких» долей.
По латыни
«minuta» - «мелкая»,
«secunda» - «вторая».
Отсюда и названия «минута» и «секунда» для долей градуса.
По латыни
«minuta» - «мелкая»,
«secunda» - «вторая».
Отсюда и названия «минута» и «секунда» для долей градуса.
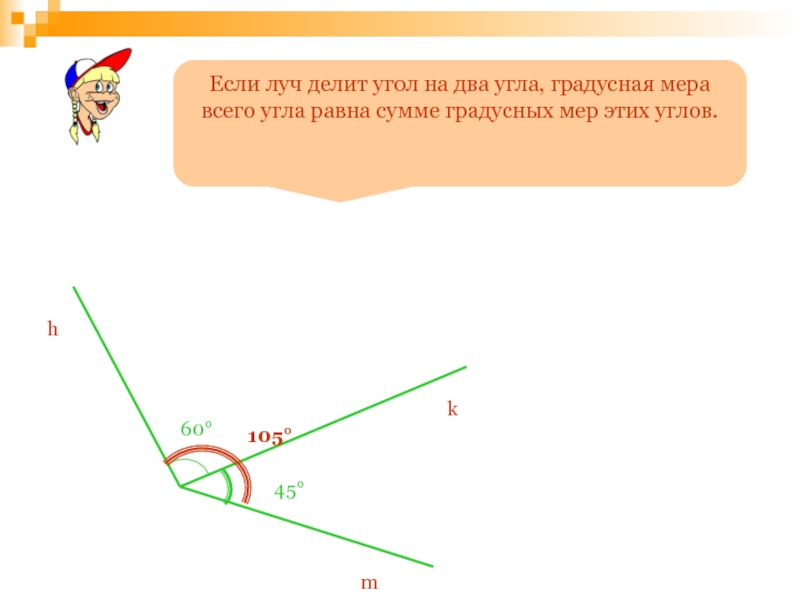
Слайд 122Если луч делит угол на два угла, градусная мера всего угла
равна сумме градусных мер этих углов.
h
k
m
60°
45°
105°
Слайд 125 - Хотел бы проходить между твоими сторонами. Что нужно сделать мне
для этого?
- С моей вершиной совмести точку свою начальную. Пересеки отрезок с концами на сторонах моих. Как видишь очень просто.
- Но если ты развернутый?
- Тогда исполнить первое достаточно. Да только не совпади с моей стороною.
- Мне понятно, но как узнать, развернутый ли ты?
- Коль до прямой дополнили друг друга стороны мои, то я развернутый, а если нет- то нет.
- Теперь я знаю, как мне быть.
- С моей вершиной совмести точку свою начальную. Пересеки отрезок с концами на сторонах моих. Как видишь очень просто.
- Но если ты развернутый?
- Тогда исполнить первое достаточно. Да только не совпади с моей стороною.
- Мне понятно, но как узнать, развернутый ли ты?
- Коль до прямой дополнили друг друга стороны мои, то я развернутый, а если нет- то нет.
- Теперь я знаю, как мне быть.
Угадай персонажей, ведущих данный диалог.
Слайд 128
120° – 32° =
38,5 °+ 85° =
29,5° ● 3
=
145° – (42°-40°) =
171° : 9=
28 ° ● 6 – 12° ● 5 – 32′ ● 3 =
145° – (42°-40°) =
171° : 9=
28 ° ● 6 – 12° ● 5 – 32′ ● 3 =
Произведите вычисления:
Слайд 129
Выполните в тетрадях практическую работу:
Начертите тупой угол АВС.
Постройте биссектрису ВD угла
АВС.
Проведите луч ВО, делящий угол DBC на два неравных угла.
Заполните таблицу:
Проведите луч ВО, делящий угол DBC на два неравных угла.
Заполните таблицу:
Слайд 134
Подготовьте ответы на следующие вопросы:
Что принимают за единицу измерения углов?
Чему равен
1 градус?
Что называют градусной мерой угла?
Какие названия носят определенные части угла? Чему они равны?
Какие градусные меры имеют равные углы?
Чему равен развернутый угол?
Какой угол называется прямым?
Какой угол называется острым?
Какой угол называется тупым?
Что называют градусной мерой угла?
Какие названия носят определенные части угла? Чему они равны?
Какие градусные меры имеют равные углы?
Чему равен развернутый угол?
Какой угол называется прямым?
Какой угол называется острым?
Какой угол называется тупым?
Слайд 135Проверка домашнего задания:
№ 49
О
С
А
В
?
155°
Решение:
Пусть угол АОС = х°, тогда угол СОВ
= (х+15)°.
Тогда х + (х+15) = 155,
х = 70
Тогда х + (х+15) = 155,
х = 70
Слайд 136Проверка домашнего задания:
№ 50
О
С
А
В
?
108°
Решение:
Пусть угол СОВ = 3х, тогда угол АОВ
= х.
Составим уравнение:
4х = 108,
х = 27
Угол СОВ = 3 ∙ 27 = 81 (градус)
Составим уравнение:
4х = 108,
х = 27
Угол СОВ = 3 ∙ 27 = 81 (градус)
Слайд 137Проверка домашнего задания:
№ 52
Решение:
Угол XOZ = угол UOV +угол ZOV +
угол UOX = 80° +80° = 160°
Слайд 138
Два угла, у которых одна сторона общая, а две другие являются
продолжением одна другой, называются смежными.
А
О
В
С
Как вы думаете, чему равна сумма смежных углов?
Слайд 139
Два угла называются вертикальными, если стороны одного угла являются продолжением сторон
другого.
1
2
3
4
Вертикальные углы равны.
Слайд 140
Опиши словесно чертеж и объясни, почему, если один угол прямой, то
остальные тоже прямые.
1
2
3
4
Слайд 141
Две прямые называются перпендикулярными, если они образуют четыре прямых угла.
АС
BD
«Прямая АС
перпендикулярна к прямой BD»
A
С
В
D
Знак ┴ для обозначения перпендикулярности ввел П. Эригон (1634)
Слайд 142
Перпендикуляр – от латинского слова “perpendicularis” («отвесный»)
(Дело в том, что с
давних времен строители для получения прямых углов пользовались отвесами – грузиками на длинной веревке)
Слайд 146
Нарисуйте три пары различных смежных углов.
Обозначьте их 1 и 2.
Измерьте градусные меры данных смежных углов.
Вычислите сумму каждой пары смежных углов.
Заполните таблицу. Сделайте вывод.
Выполните в тетради практическую работу.
Слайд 147
Нарисуйте 3 пары пересекающихся прямых.
Обозначьте в них пары вертикальных углов
1, 2, 3, 4.
Измерьте градусные меры этих углов.
Результаты измерений занесите в таблицу. Сравните угол 1 с углом 3, угол 2 с углом 4.
Сделайте вывод.
Измерьте градусные меры этих углов.
Результаты измерений занесите в таблицу. Сравните угол 1 с углом 3, угол 2 с углом 4.
Сделайте вывод.
Слайд 148
Даны смежные углы и три утверждения о них:
один из них
на 90° больше другого;
их градусные меры относятся как 4 : 5;
один из них в 3 раза меньше другого.
Одно из этих утверждений противоречит двум другим. Найдите его.
их градусные меры относятся как 4 : 5;
один из них в 3 раза меньше другого.
Одно из этих утверждений противоречит двум другим. Найдите его.
Слайд 149
Собери 5 бананов (выбери нужный ответ).
Угол АОВ смежный с углом ВОС.
Найди
угол АОВ, если
Угол АОВ меньше угла ВОС на 40°
70°
110°
35°
Угол АОВ больше угла ВОС на 120°
Угол АОВ больше угла ВОС на 47°18´
Угол АОВ в 3 раза меньше угла ВОС
Угол АОВ относится к углу ВОС, как 5 к 4.
150°
30°
100°
113°39´
66°21´
140°21´
135°
45°
75°
90°
100°
80°
Слайд 153
Подготовьте ответы на следующие вопросы:
Какие углы называются смежными?
Чему равна сумма смежных
углов?
Какие углы называются вертикальными?
Какие прямые называются перпендикулярными?
Пересекаются ли две прямые, перпендикулярные к третьей?
Какие углы называются вертикальными?
Какие прямые называются перпендикулярными?
Пересекаются ли две прямые, перпендикулярные к третьей?
Слайд 154Проверка домашнего задания:
№ 67
Решение:
3
2
1
4
Угол 3 и угол 4 равны, как вертикальные.
Угол
1 + угол 2 + угол 3 = 180°, так как вместе составляют развернутый угол.
Слайд 155№ 68
Проверка домашнего задания:
O
A
B
C
D
E
F
50°
70°
Решение:
Угол ВОС = углу FOC = 70° (как
вертикальные)
Угол АОВ = углу EOD = 50° (как вертикальные).
Угол АОС = 70° + 50° = 120°
Угол BOD = 70° + 60° = 130°
Угол СОЕ = 60° +50° = 110°
Угол СОD = 180° - 70° - 50° = 60°
Угол АОВ = углу EOD = 50° (как вертикальные).
Угол АОС = 70° + 50° = 120°
Угол BOD = 70° + 60° = 130°
Угол СОЕ = 60° +50° = 110°
Угол СОD = 180° - 70° - 50° = 60°
Слайд 161Ответьте на следующие вопросы:
Один из смежных углов прямой, каким (острым, тупым
или прямым) будет другой угол?
Верно ли, что, если смежные углы равны, то они прямые?
Даны два равных угла. Равны ли смежные с ними углы?
Верно ли, что, если смежные углы равны, то они прямые?
Даны два равных угла. Равны ли смежные с ними углы?
Слайд 164
Выполните
самостоятельную работу.
Найдите углы 1, 2, 3, 4
2
1
3
140°
60°
1
2
3
4
1
3
70°
4
60°
1
2
3
4
1 вариант
2 вариант
