- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по стереометрии Тела вращения-теория
Содержание
- 1. Презентация по стереометрии Тела вращения-теория
- 2. Содержание:ЦилиндрКонус и усечённый конусШар и сфера
- 3. ЦилиндрОпределение:Тело, которое образуется при вращении прямоугольника вокруг
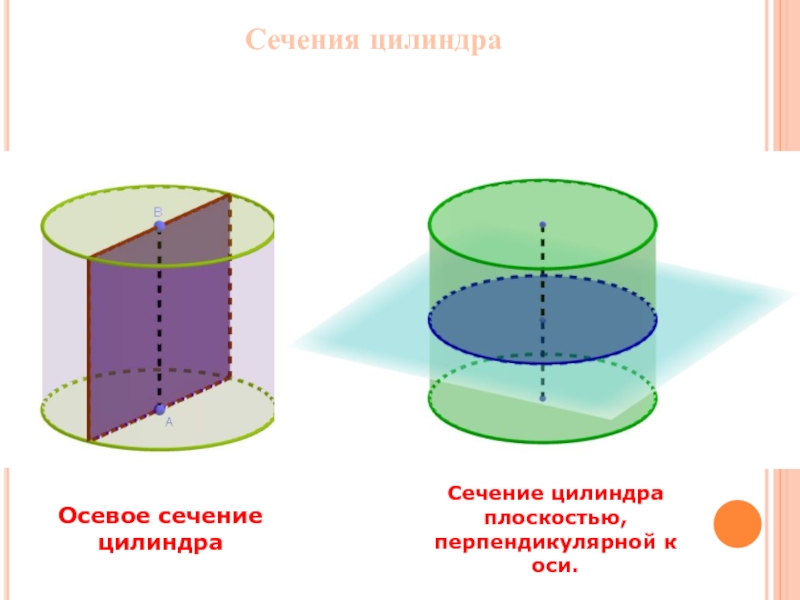
- 4. Сечения цилиндраОсевое сечение цилиндраСечение цилиндра плоскостью, перпендикулярной к оси.
- 5. Радиус основания цилиндра равен 4, а диагональ
- 6. Радиус основания цилиндра равен 3. Диагональ осевого
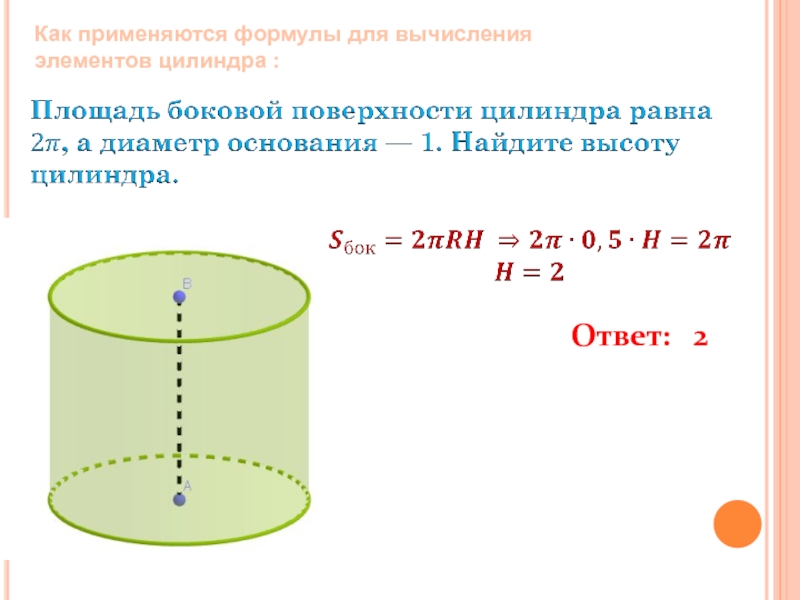
- 7. Ответ: 2Как применяются формулы для вычисления элементов цилиндра :
- 8. КонусОпределение: Тело, которое образуется при вращении прямоугольного
- 9. Сечения конусаЕсли секущая плоскость проходит через ось
- 10. Высота конуса равна 4, а длина образующей —
- 11. Высота конуса равна 4. Образующая наклонена к
- 12. Задача 1:Высота конуса равна 6, а угол
- 13. Как применяются формулы для вычисления элементов конуса:
- 14. Как применяются формулы для вычисления элементов конуса:
- 15. Усеченный конус Часть конуса, ограниченная
- 16. Усеченный прямой конус
- 17. Шар – тело вращенияOS, ON, OC, OD
- 18. Сечение шара плоскостьюВсякое сечение шара плоскостью есть
- 19. Касательная плоскость к шаруПлоскость, проходящая через точку
- 20. Шар называется описанным около многогранника, если все
- 21. Шаровым сегментом называется часть шара, отсекаемая от
- 22. Высотой сегмента шара является длина отрезка диаметра, перпендикулярного к секущей плоскости О1О2. Шаровой сегмент
- 23. Шаровым слоем называется часть шара, заключенная между
- 24. Высотой шарового слоя является расстояние между плоскостями О1О2.Шаровой слой
- 25. Шаровым сектором называется тело, полученное вращением кругового
- 26. Найдите радиус сферы, вписанной в куб, ребра
- 27. Найдите образующую цилиндра, описанного около сферы радиуса
- 28. Найдите квадрат диаметра сферы, описанной около прямоугольного
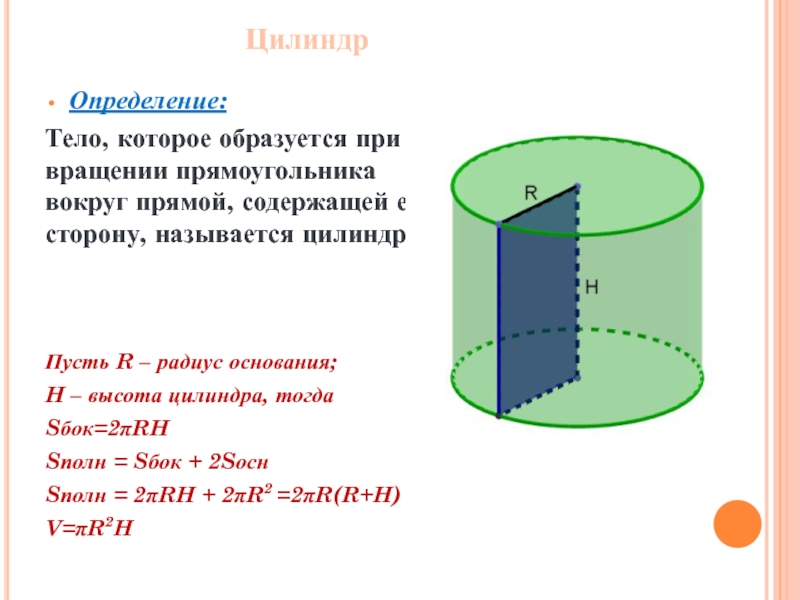
Слайд 3Цилиндр
Определение:
Тело, которое образуется при вращении прямоугольника вокруг прямой, содержащей его сторону,
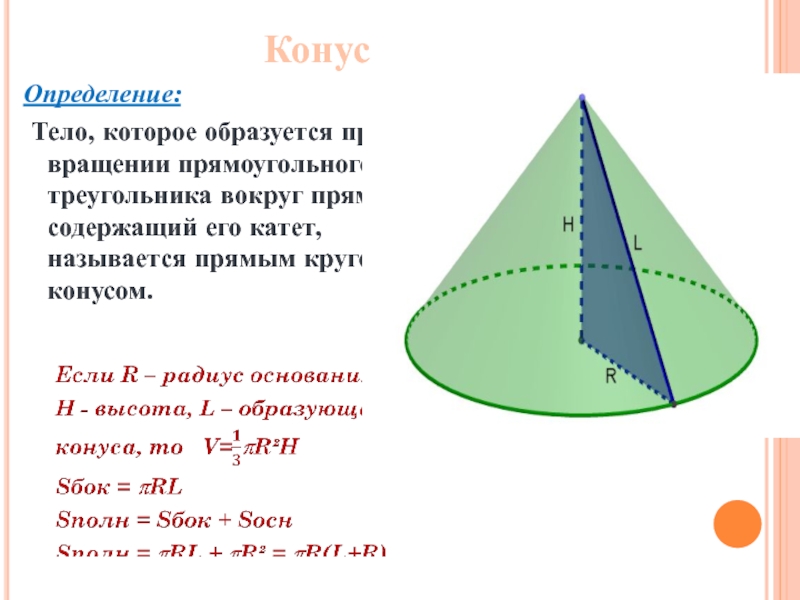
Пусть R – радиус основания;
H – высота цилиндра, тогда
Sбок=2RH
Sполн = Sбок + 2Sосн
Sполн = 2RH + 2R2 =2R(R+H)
V=R2H
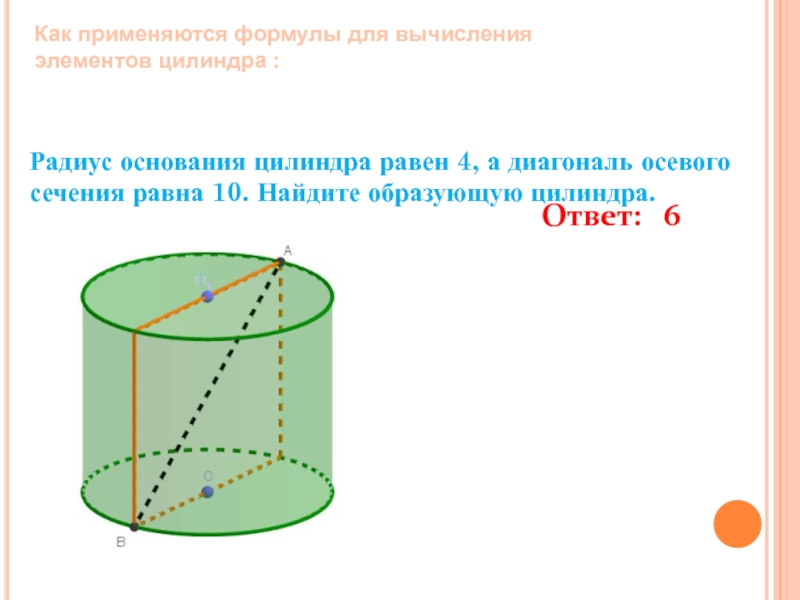
Слайд 5Радиус основания цилиндра равен 4, а диагональ осевого сечения равна 10.
Ответ: 6
Как применяются формулы для вычисления элементов цилиндра :
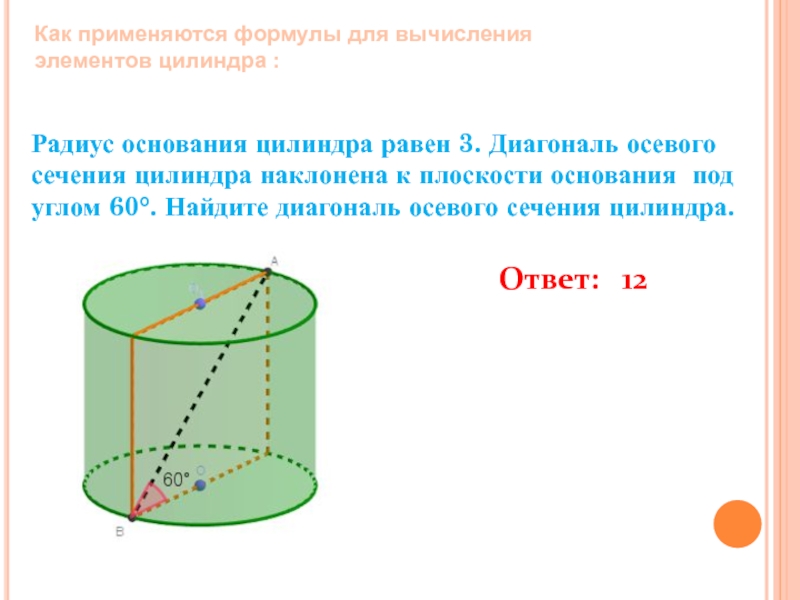
Слайд 6Радиус основания цилиндра равен 3. Диагональ осевого сечения цилиндра наклонена к
Ответ: 12
Как применяются формулы для вычисления элементов цилиндра :
Слайд 8Конус
Определение:
Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащий
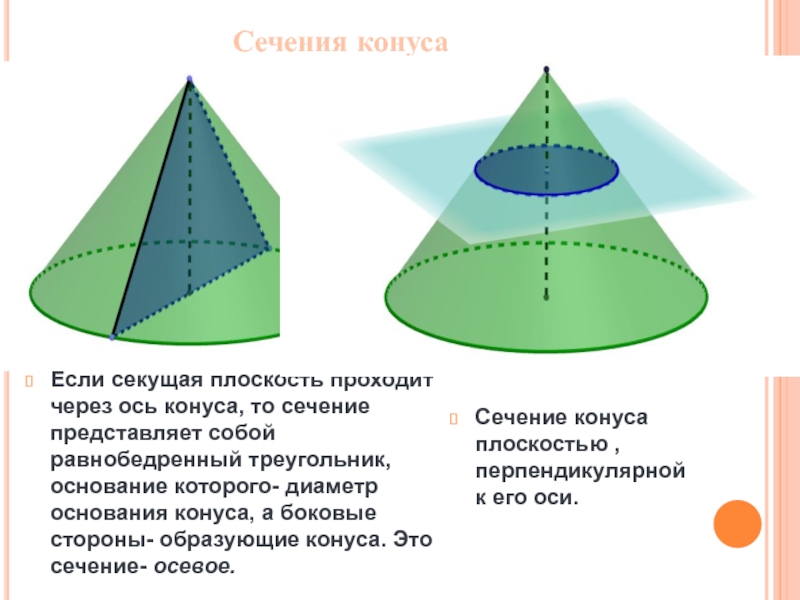
Слайд 9Сечения конуса
Если секущая плоскость проходит через ось конуса, то сечение представляет
Сечение конуса плоскостью , перпендикулярной к его оси.
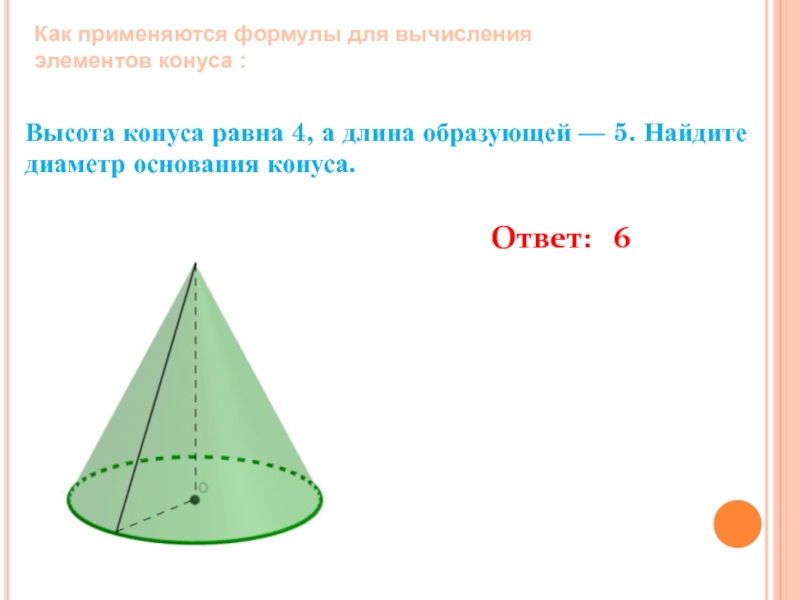
Слайд 10Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания
Ответ: 6
Как применяются формулы для вычисления элементов конуса :
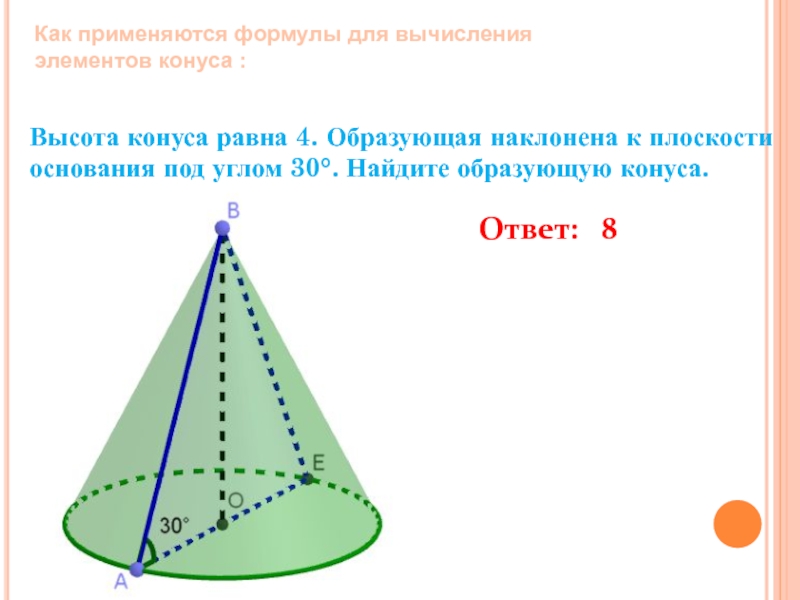
Слайд 11Высота конуса равна 4. Образующая наклонена к плоскости основания под углом
Ответ: 8
Как применяются формулы для вычисления элементов конуса :
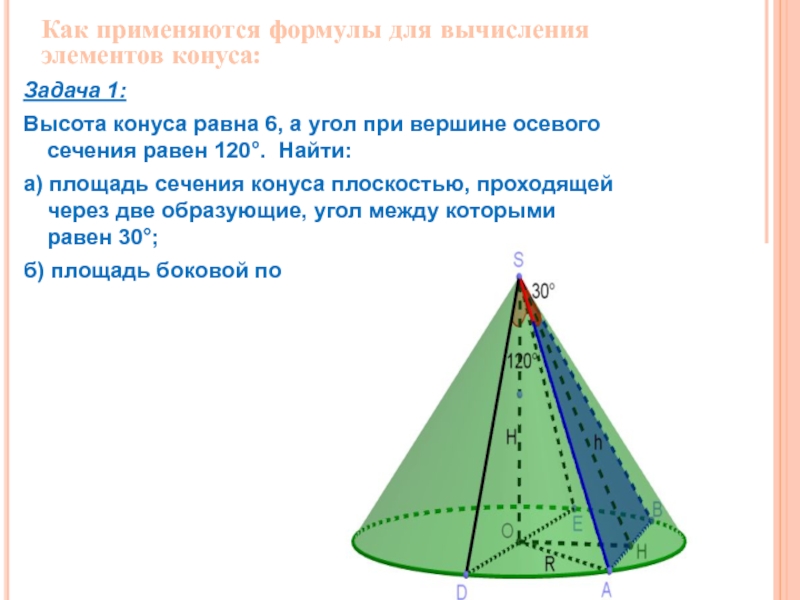
Слайд 12Задача 1:
Высота конуса равна 6, а угол при вершине осевого сечения
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30°;
б) площадь боковой поверхности конуса.
Как применяются формулы для вычисления элементов конуса:
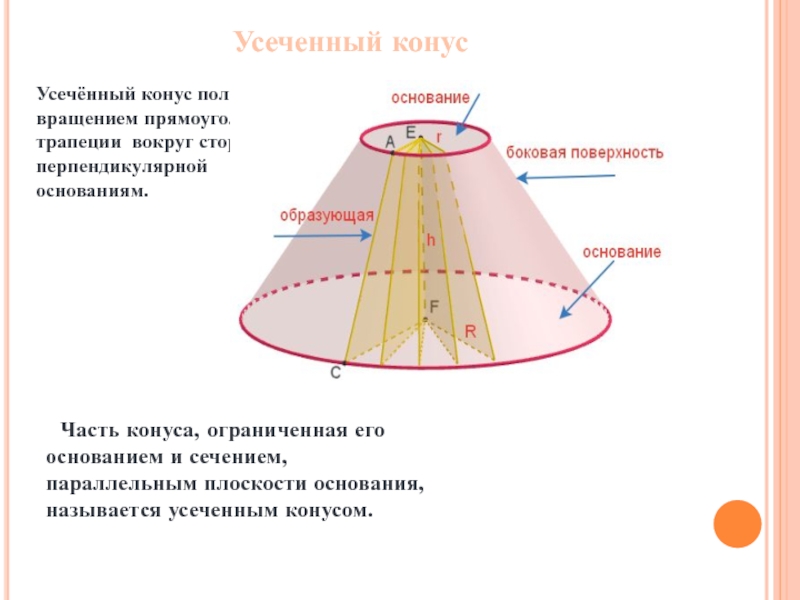
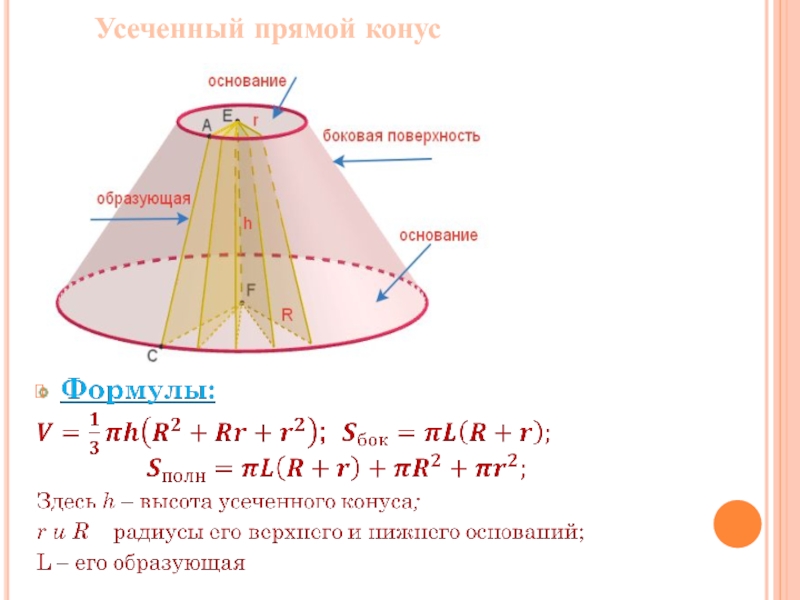
Слайд 15Усеченный конус
Часть конуса, ограниченная его основанием и сечением,
Усечённый конус получен вращением прямоугольной трапеции вокруг стороны, перпендикулярной основаниям.
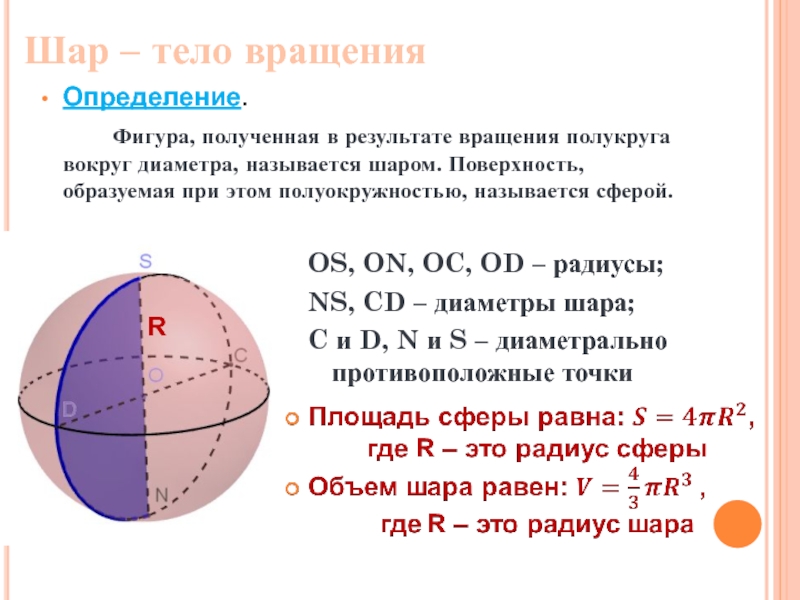
Слайд 17Шар – тело вращения
OS, ON, OC, OD – радиусы;
NS, CD –
C и D, N и S – диаметрально противоположные точки
Определение.
Фигура, полученная в результате вращения полукруга вокруг диаметра, называется шаром. Поверхность, образуемая при этом полуокружностью, называется сферой.
R
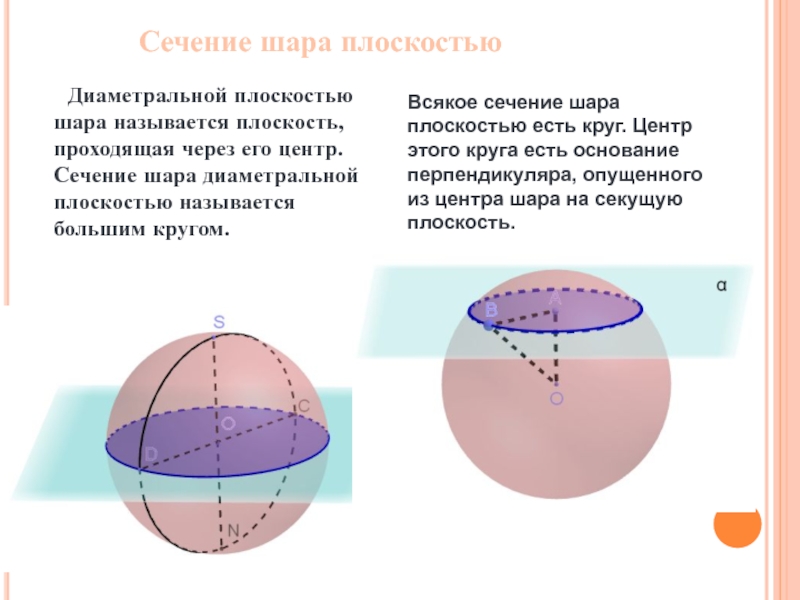
Слайд 18Сечение шара плоскостью
Всякое сечение шара плоскостью есть круг. Центр этого круга
Диаметральной плоскостью шара называется плоскость, проходящая через его центр. Сечение шара диаметральной плоскостью называется большим кругом.
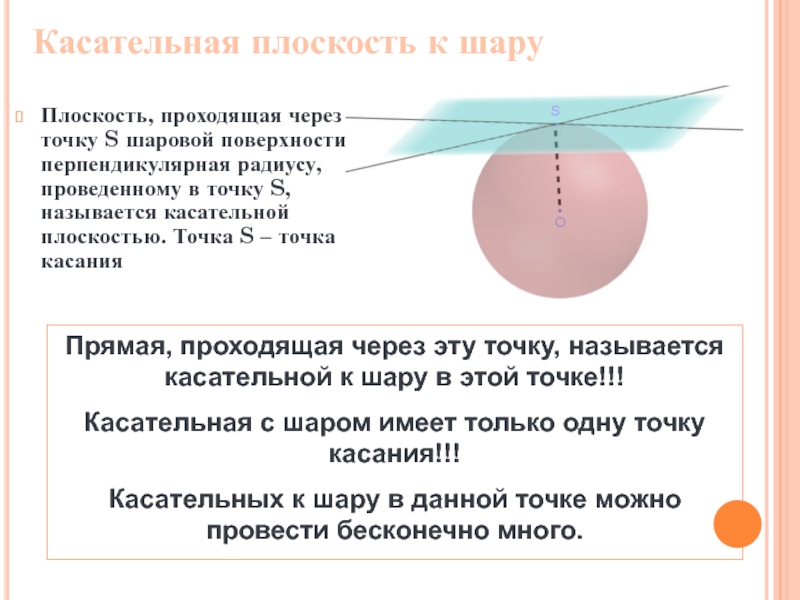
Слайд 19Касательная плоскость к шару
Плоскость, проходящая через точку S шаровой поверхности и
Прямая, проходящая через эту точку, называется касательной к шару в этой точке!!!
Касательная с шаром имеет только одну точку касания!!!
Касательных к шару в данной точке можно провести бесконечно много.
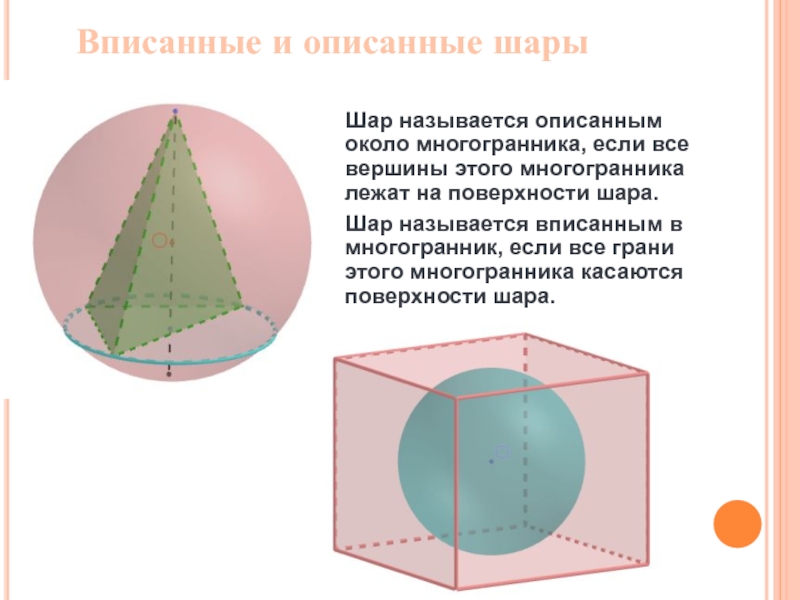
Слайд 20Шар называется описанным около многогранника, если все вершины этого многогранника лежат
Шар называется вписанным в многогранник, если все грани этого многогранника касаются поверхности шара.
Вписанные и описанные шары
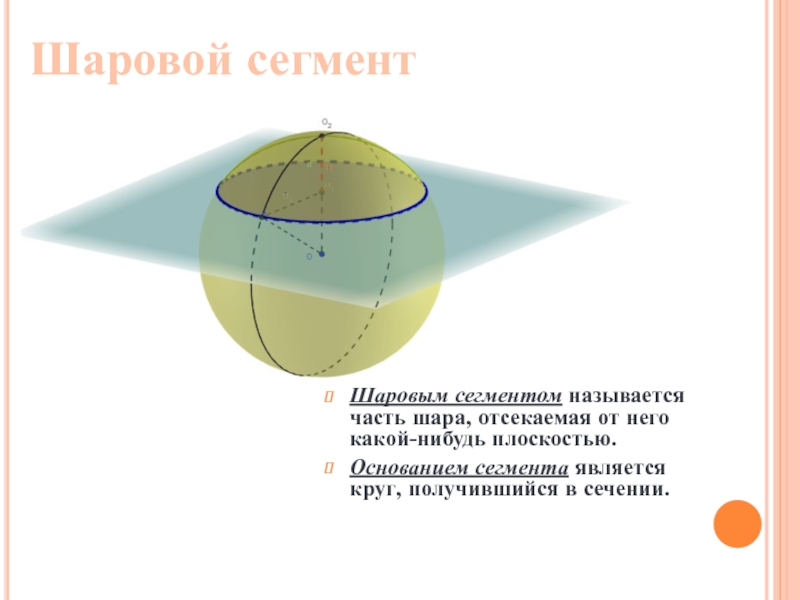
Слайд 21Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Основанием сегмента
Шаровой сегмент
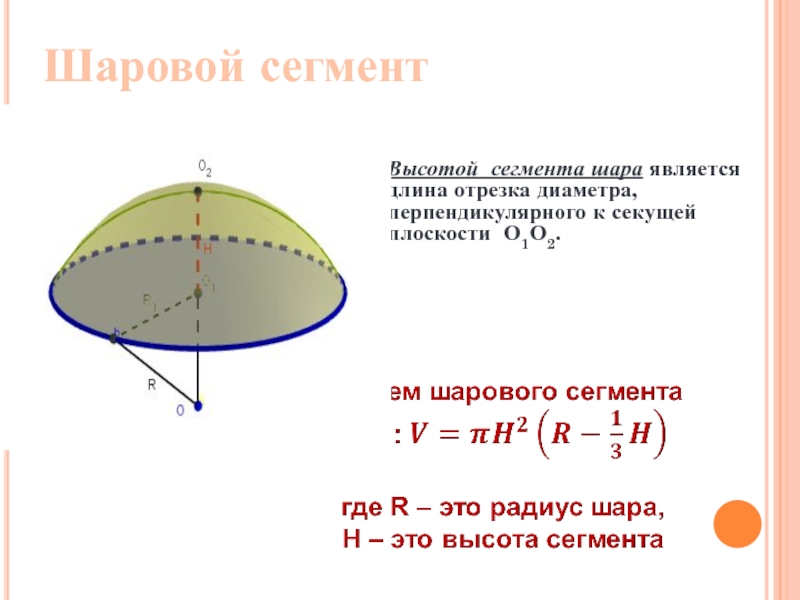
Слайд 22Высотой сегмента шара является длина отрезка диаметра, перпендикулярного к секущей плоскости
Шаровой сегмент
Слайд 23
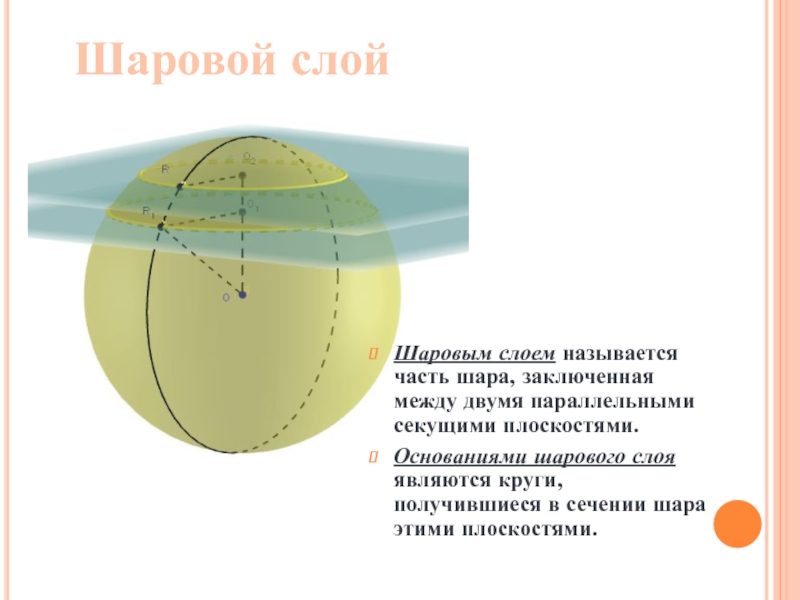
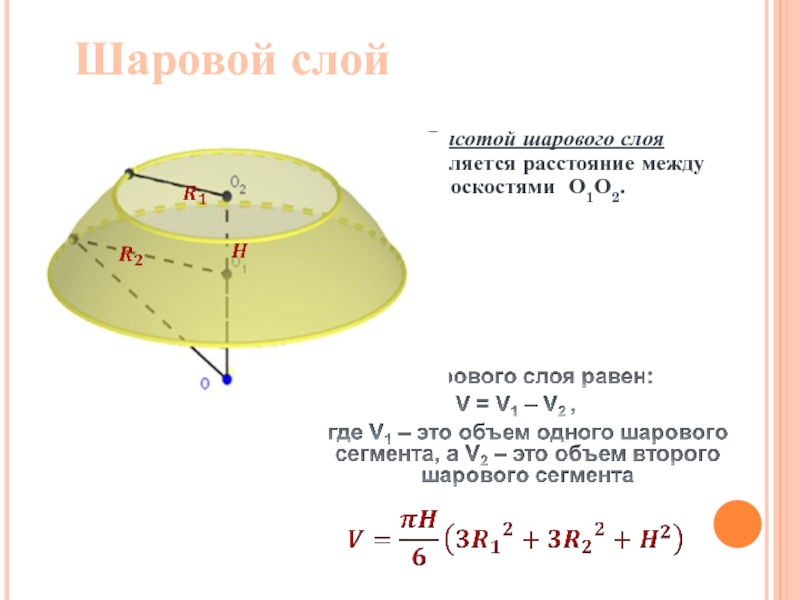
Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.
Основаниями
Шаровой слой
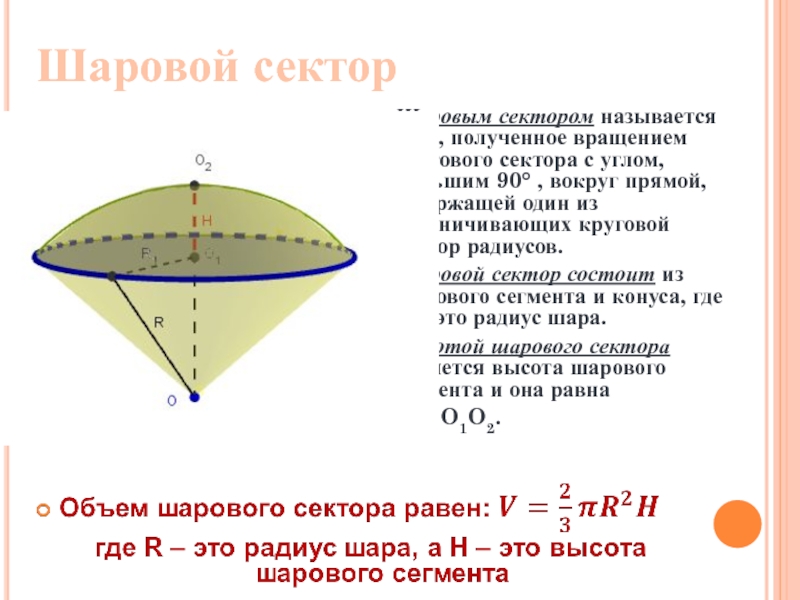
Слайд 25Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим
Шаровой сектор состоит из шарового сегмента и конуса, где R – это радиус шара.
Высотой шарового сектора является высота шарового сегмента и она равна
H = O1O2.
Шаровой сектор
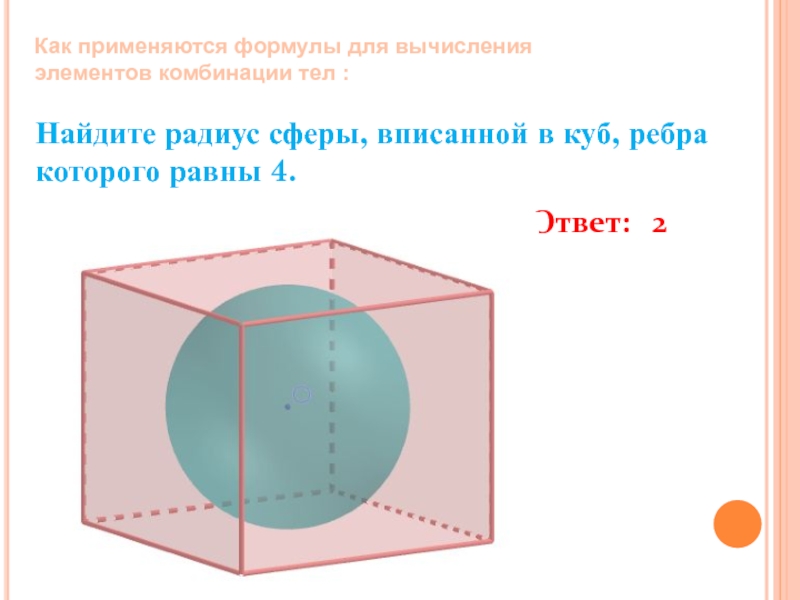
Слайд 26Найдите радиус сферы, вписанной в куб, ребра которого равны 4.
Ответ:
Как применяются формулы для вычисления элементов комбинации тел :
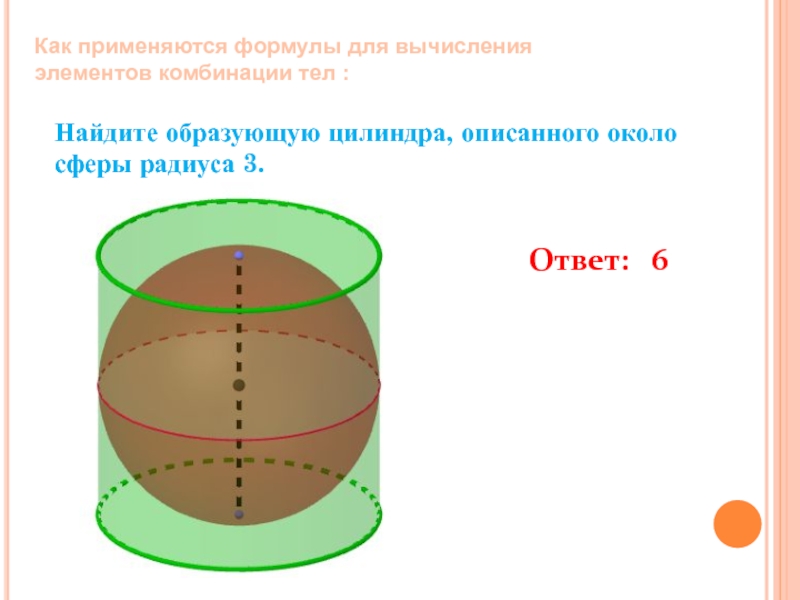
Слайд 27Найдите образующую цилиндра, описанного около сферы радиуса 3.
Ответ: 6
Как применяются
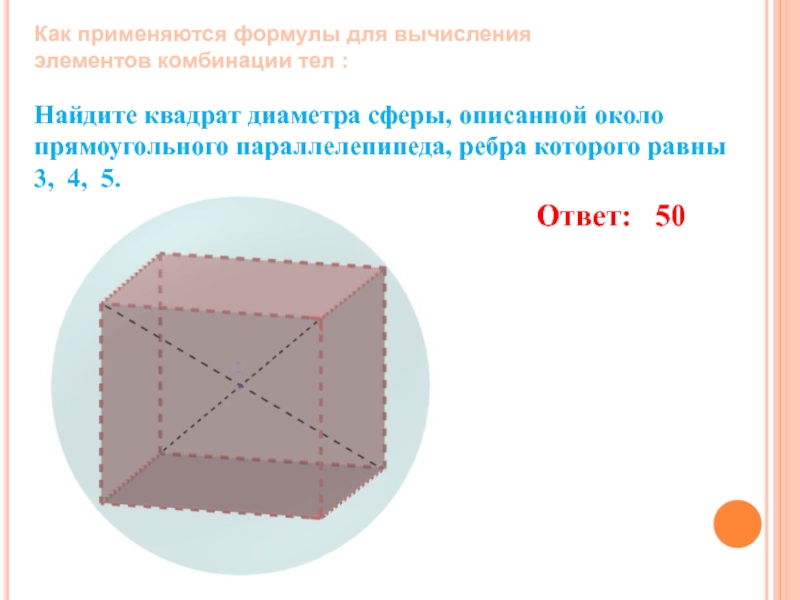
Слайд 28Найдите квадрат диаметра сферы, описанной около прямоугольного параллелепипеда, ребра которого равны
Ответ: 50
Как применяются формулы для вычисления элементов комбинации тел :