- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темуРешение прикладных задач по геометрии
Содержание
- 1. Презентация по математике на темуРешение прикладных задач по геометрии
- 2. Типология заданийСпицы и часыТеорема ПифагораПодобие треугольниковВычисление длин и площадейРазные задачи
- 3. Тип 1. Спицы и часы (теория)Циферблат
- 4. Тип 1. Спицы и часы Задача 1Колесо
- 5. Тип 1. Спицы и часы Задача 2Сколько
- 6. Тип 1. Спицы и часы Задача 3
- 7. Тип 1. Спицы и часы Задача 4Какой
- 8. Тип 1. Спицы и часы Задача 5
- 9. Тип 1. Часы и спицы Задача 6На
- 10. Тип 1. Спицы и часы Задачи для
- 11. Тип 2. Теорема Пифагора1) Увидеть прямоугольный треугольник2)
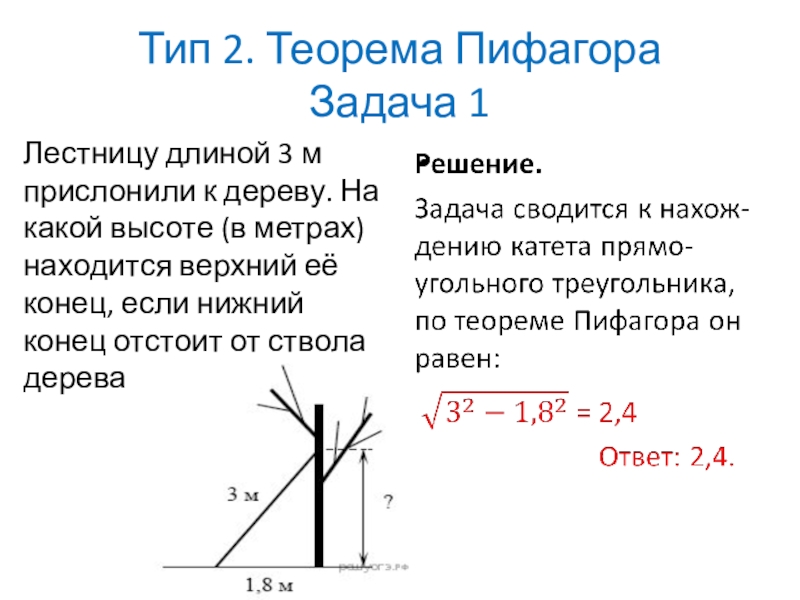
- 12. Тип 2. Теорема Пифагора Задача 1Лестницу длиной
- 13. Тип 2. Теорема Пифагора Задача 2Мальчик прошел
- 14. Тип 2. Теорема Пифагора Задача 3Мальчик и
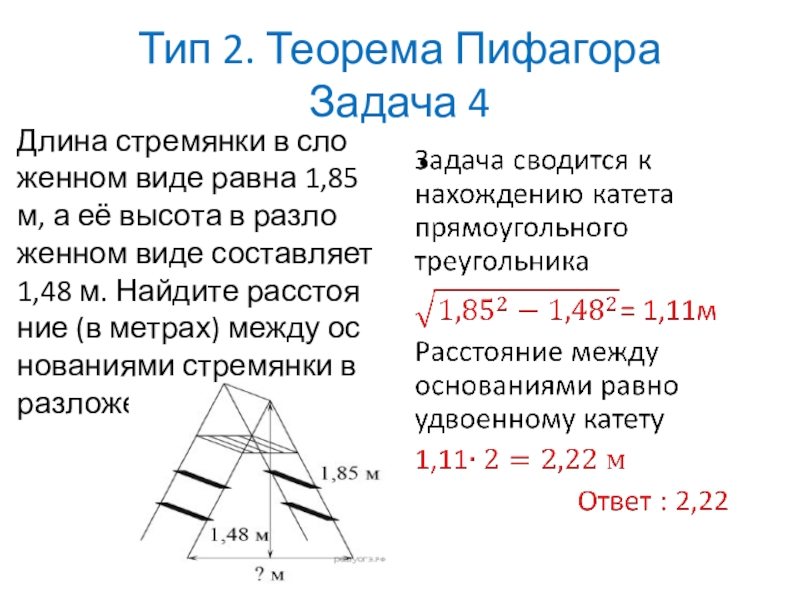
- 15. Тип 2. Теорема Пифагора Задача 4Длина стремянки
- 16. Тип 2. Теорема Пифагора Задача 5От столба
- 17. Тип 2. Теорема Пифагора Задача 6Лестница соединяет
- 18. Тип 2. Теорема Пифагора Задачи для самостоятельного
- 19. Тип 3. Подобие треугольников1) Увидеть подобные треугольники2)
- 20. Тип 3. Подобие треугольников1) Увидеть подобные треугольники2)
- 21. Тип 3. Подобие треугольников1) Увидеть подобные треугольники2)
- 22. Тип 3. Подобие треугольников Задача 1Человек ростом
- 23. Тип 3. Подобие треугольников Задача 2На каком
- 24. Тип 3. Подобие треугольников Задача 3Проектор полностью
- 25. Задачи для самостоятельного решенияЧеловек, рост которого равен
- 26. Тип 4. Нахождение длин и площадей Задача
- 27. Тип 4. Нахождение длин и площадей Задача
- 28. Тип 4. Нахождение длин и площадей Задача
- 29. Тип 4. Нахождение длин и площадей Задача
- 30. Тип 4. Нахождение длин и площадей Задача
- 31. Тип 4. Нахождение длин и площадей
- 32. Тип 4. Нахождение длин и площадей
- 33. Задачи для самостоятельного решенияСколько потребуется кафельных плиток
Слайд 2Типология заданий
Спицы и часы
Теорема Пифагора
Подобие треугольников
Вычисление длин и площадей
Разные задачи
Слайд 3Тип 1. Спицы и часы
(теория)
Циферблат и колесо
представляют собой – круг,
2. Шкала часов разбита на … часов и на … минут, поэтому
1час – это …. градусов, а
1 минута – это … градусов
Слайд 4Тип 1. Спицы и часы
Задача 1
Колесо имеет 18 спиц. Найдите величину
Решение.
Колесо представляет собой круг, 18 спиц которого делят на 18 круговых секторов. Так как развёрнутый угол равен 360° для каждого из секторов имеем:
360: 18=20
Ответ: 20.
Слайд 5Тип 1. Спицы и часы
Задача 2
Сколько спиц в колесе, если угол
Решение.
Колесо представляет собой круг. Количество спиц совпадает с количеством секторов на которые ими оно делится. Так как развёрнутый угол 360°, а угол между спицами равен 24°, имеем:
360:24=15
Ответ: 15.
Слайд 6Тип 1. Спицы и часы
Задача 3
Какой угол (в градусах) описывает
Решение:
Минутными делениями циферблат разбит на 60 круговых секторов. Угол каждого из них равен 360° : 60 = 6°. За 10 минут минутная стрелка проходит 10 · 6° = 60°.
Ответ: 60.
Слайд 7Тип 1. Спицы и часы
Задача 4
Какой угол (в градусах) образуют минутная
Слайд 9Тип 1. Часы и спицы
Задача 6
На сколько градусов повернется Земля вокруг
Решение.
За сутки Земля совершает полный оборот, то есть поворачивается на 360°. Следовательно, за один час Земля поворачивается на 360° : 24 = 15°. Получаем, что за 7 часов Земля поворачивается на 7 · 15° = 105°.
Ответ: 105.
Слайд 10Тип 1. Спицы и часы
Задачи для самостоятельного решения
1) Колесо имеет 15
2) Найдите угол, который образуют минутная и часовая стрелки часов в 7:00. Ответ дайте в градусах
3) Найдите угол, который минутная стрелка описывает за 13 минут. Ответ дайте в градусах
4) На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 14°?
5) За сколько часов Земля повернется вокруг своей оси на 120°?
Слайд 11Тип 2. Теорема Пифагора
1) Увидеть прямоугольный треугольник
2) Записать для него теорему
3) Сопоставить результат и вопрос задачи
Катет в квадрате плюс катет в квадрате равно гипотенуза в квадрате
Или
Катет в квадрате равен гипотенуза в квадрате минус катет в квадрате
Слайд 12Тип 2. Теорема Пифагора
Задача 1
Лестницу длиной 3 м прислонили к дереву.
Слайд 13Тип 2. Теорема Пифагора
Задача 2
Мальчик прошел от дома по направлению на
Слайд 14Тип 2. Теорема Пифагора
Задача 3
Мальчик и девочка, расставшись на перекрестке, пошли
Слайд 15Тип 2. Теорема Пифагора
Задача 4
Длина стремянки в сложенном виде равна 1,85
Слайд 16Тип 2. Теорема Пифагора
Задача 5
От столба высотой 9 м к дому
Слайд 17Тип 2. Теорема Пифагора
Задача 6
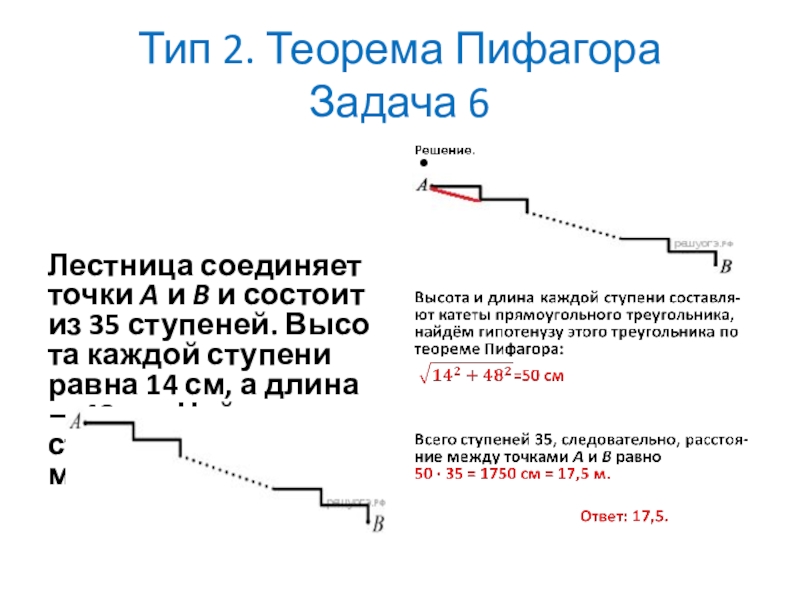
Лестница соединяет точки A и B и состоит из 35 ступеней.
Слайд 18Тип 2. Теорема Пифагора
Задачи для самостоятельного решения
1) Пожарную лестницу длиной 13 м приставили к
2) Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 6,3 м от земли. Длина троса равна 6,5 м. Найдите расстояние от точки основания флагштока до места крепления троса на земле. Ответ дайте в метрах.
3) Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?
4) От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Слайд 19Тип 3. Подобие треугольников
1) Увидеть подобные треугольники
2) Записать для них отношение
3) Решить полученную пропорцию
4) Сопоставить результат и вопрос задачи
Признаки подобия треугольников:
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны( по двум углам)
Слайд 20Тип 3. Подобие треугольников
1) Увидеть подобные треугольники
2) Записать для них отношение
3) Решить полученную пропорцию
3) Сопоставить результат и вопрос задачи
Признаки подобия треугольников:
2) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны
Слайд 21Тип 3. Подобие треугольников
1) Увидеть подобные треугольники
2) Записать для них отношение
3) Решить полученную пропорцию
3) Сопоставить результат и вопрос задачи
Признаки подобия треугольников:
3) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
Слайд 22Тип 3. Подобие треугольников
Задача 1
Человек ростом 1,7 м стоит на расстоянии
Слайд 23Тип 3. Подобие треугольников
Задача 2
На каком расстоянии (в метрах) от фонаря
Слайд 24Тип 3. Подобие треугольников
Задача 3
Проектор полностью освещает экран A высотой 80 см,
Слайд 25Задачи для самостоятельного решения
Человек, рост которого равен 1,8 м, стоит на
(в метрах).
2) Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются
неизменными?
Слайд 26Тип 4. Нахождение длин и площадей
Задача 1
Площадь прямоугольного земельного участка равна
Решение.
Переведем площадь участка в квадратные метры: 9 га = 90 000 м2.
Площадь прямоугольника равна произведению его смежных сторон. Поэтому, длина участка равна: 90 000 : 150 = 600 м.
Ответ: 600.
Слайд 27Тип 4. Нахождение длин и площадей
Задача 2
Найдите периметр прямоугольного участка земли,
Слайд 28Тип 4. Нахождение длин и площадей
Задача 3
Сколько досок длиной 3,5 м,
Решение.
Найдем объем доски : 350 · 20 · 2 = 14 000 см3.
Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см3.
Поэтому количество досок равно 1 260 000 : 14 000 = 90.
Ответ: 90.
Слайд 29Тип 4. Нахождение длин и площадей
Задача 4
Пол комнаты, имеющей форму прямоугольника
Решение.
Площадь всей комнаты равна 4 · 9 = 36 м2.
Площадь одной дощечки 0,1 · 0,25 = 0,025 м2.
Получаем, что потребуется 36 : 0,025 = 1440 дощечек.
Ответ: 1440.
Слайд 30Тип 4. Нахождение длин и площадей
Задача 5
Две трубы, диаметры которых равны
Слайд 31Тип 4. Нахождение длин и площадей
Задача 6
Сколько досок длиной 4 м,
Решение.
Переведём все длины в метры.
Объём бруса равен 8 · 0,3 · 0,4 = 0,96 м3.
Объём одной доски 4 · 0,2 · 0,03 = 0,024 м3.
Получаем, что из бруса получится 0,96 : 0,024 = 40 досок.
Ответ: 40.
Слайд 32Тип 4. Нахождение длин и площадей
Задача 7
Наклонная крыша установлена на
средней
опоры.
Слайд 33Задачи для самостоятельного решения
Сколько потребуется кафельных плиток квадратной формы со стороной
Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30×50×90 (см) можно поместить в кузов машины размером 2,4×3×2,7 (м)?
Девочка прошла от дома по направлению на запад 340 м. Затем повернула на север и прошла 60 м. После этого она повернула на восток и прошла ещё 420 м. На каком расстоянии (в метрах) от дома оказалась девочка?
Определите высоту дома, ширина фасада
которого равна 8 м, высота от фундамента до
крыши равна 4 м, а длина ската крыши равна 5 м.