Новиковой
Никулина С.И.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темуМодуль геометрия .Треугольники
Содержание
- 1. Презентация по математике на темуМодуль геометрия .Треугольники
- 2. Высота, медиана, биссектриса треугольникаОтрезок, соединяющий вершину треугольника
- 3. Средняя линия треугольникаСредней линией треугольника называется отрезок,
- 4. Cерединный перпендикулярСерединным перпендикуляром к отрезку называется прямая,
- 5. Точка пересечения серединных перпендикуляровСерединные перпендикуляры к сторонам
- 6. Точка пересечения биссектрис треугольникаБиссектрисы треугольника пересекаются в одной точкеАВСКСК – биссектриса
- 7. Точка пересечения высот треугольникаВысоты треугольника (или их продолжения) пересекаются в одной точкеАСВКМРОО – точка пересечения высот
- 8. Точка пересечения медиан треугольникаМедианы треугольника пересекаются в
- 9. Равнобедренный треугольникРавносторонний треугольникТреугольник называется равнобедренным, если две
- 10. Свойства равнобедренного треугольникаАСВВ равнобедренном треугольнике углы при основании равны
- 11. Прямоугольный треугольникТреугольник, у которого один из углов
- 12. Свойства прямоугольного треугольникаСумма двух острых углов прямоугольного
- 13. Признаки равенства треугольниковI признакПо двум сторонам и
- 14. Признаки равенства прямоугольных треугольниковПо двум катетамЕсли АВ
- 15. Неравенство треугольникаКаждая сторона треугольника меньше суммы двух
- 16. Сумма углов треугольника равна 180°ABC
- 17. Слайд 17
- 18. Зависимость между величинами сторон и углов треугольникаВ
- 19. Теорема ФалесаЕсли на одной из двух прямых
- 20. Подобие треугольниковДва треугольника называются подобными, если их
- 21. Признаки подобия треугольников1. Если два угла одного
- 22. Синус, косинус, тангенс острого угла прямоугольного треугольника
- 23. sin² x + cos² x = 1Основное
- 24. Стороны треугольника пропорциональны синусам противолежащих угловТеорема синусоваbcCBA
- 25. Квадрат стороны треугольника равен сумме квадратов двух
- 26. № 9. (демонстрационный вариант 2013 г) В
- 27. №9. В треугольнике АВС АD – биссектриса,
- 28. №9. Один острый угол прямоугольного треугольника в
- 29. № 24 (демонстрационный вариант 2013 г) В
- 30. № 24. В треугольнике АВС угол С
- 31. № 25. Отрезки АВ и CD пересекаются
- 32. №25. В треугольнике АВС М – середина
- 33. № 25. В прямоугольном треугольнике KLM с
Высота, медиана, биссектриса треугольникаОтрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианойАМАМ – медианаОтрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольникаАА1АА1 – биссектрисаПерпендикуляр, проведенный из вершины треугольника к прямой,
Слайд 1Подготовка к ОГЭ
модуль «Геометрия»
Треугольники
учитель математики
МБОУ лицей №87 имени Л.И.
Слайд 2Высота, медиана, биссектриса треугольника
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны,
называется медианой
А
М
АМ – медиана
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
А
А1
АА1 – биссектриса
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется перпендикуляром
Н
А
АН - высота
Слайд 3Средняя линия треугольника
Средней линией треугольника называется отрезок, соединяющий середины двух его
сторон.
К
М
КМ – средняя линия
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
А
В
С
Слайд 4Cерединный перпендикуляр
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного
отрезка и перпендикулярна к нему
а
А
В
а – серединный перпендикуляр к отрезку АВ
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему
М
А
В
О
m
m – серединный перпендикуляр к отрезку АВ,
О – середина отрезка АВ
М Є m
АМ = ВМ
Слайд 5Точка пересечения серединных перпендикуляров
Серединные перпендикуляры к сторонам треугольника
пересекаются в одной
точке
А
В
С
m
n
p
O
m, n, p пересекаются в точке О
Слайд 6Точка пересечения биссектрис треугольника
Биссектрисы треугольника пересекаются в одной точке
А
В
С
К
СК – биссектриса
<С
М
АМ – биссектриса <А
ВР – биссектриса <В
Р
О
О – точка пересечения биссектрис
Слайд 7Точка пересечения высот треугольника
Высоты треугольника (или их продолжения) пересекаются в одной
точке
А
С
В
К
М
Р
О
О – точка пересечения высот
Слайд 8Точка пересечения медиан треугольника
Медианы треугольника пересекаются в одной точке, которая делит
каждую медиану в отношении 2:1, считая от вершины
А
В
С
К
М
Р
О
ВР , СК, АМ – медианы треугольника АВС
О – точка пересечения медиан
СО : КО = 2 : 1
АО : МО = 2 :1
ВО : РО = 2 : 1
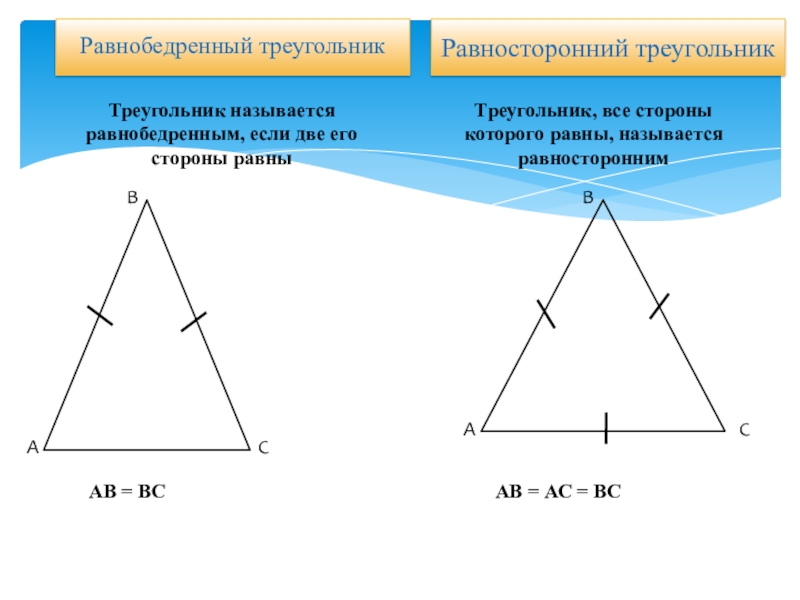
Слайд 9Равнобедренный треугольник
Равносторонний треугольник
Треугольник называется равнобедренным, если две его стороны равны
Треугольник, все
стороны которого равны, называется равносторонним
АВ = ВС
А
В
С
А
В
С
АВ = АС = ВС
Слайд 10Свойства равнобедренного треугольника
А
С
В
В равнобедренном треугольнике углы при основании равны
равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
АС = ВС
СК - биссектриса
К
АК = КВ, СК АВ
Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Слайд 11Прямоугольный треугольник
Треугольник, у которого один из углов прямой, называется прямоугольным
АВ
и АС – катеты
ВС - гипотенуза
ВС - гипотенуза
А
В
С
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
ВС² = АВ² + АС²
Слайд 12Свойства прямоугольного треугольника
Сумма двух острых углов прямоугольного треугольника равна 90°
Катет прямоугольного
треугольника, лежащий против угла в 30°, равен половине гипотенузы
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
С
А
В
Слайд 13Признаки равенства треугольников
I признак
По двум сторонам и углу между ними
II признак
По
стороне и прилежащим к ней углам
III признак
По трем сторонам
А
N
М
К
С
В
Слайд 14Признаки равенства прямоугольных треугольников
По двум катетам
Если АВ = КМ, АС =
KN,
то ∆АВС = ∆KMN
то ∆АВС = ∆KMN
А
N
М
К
С
В
По катету и прилежащему острому углу
Если AB = KM, то ∆АВС = ∆KMN
По гипотенузе и острому углу
Если ВС = MN, то ∆АВС = ∆KMN
По гипотенузе и катету
Если ВС = МN, АС = KN,
то ∆АВС = ∆KMN
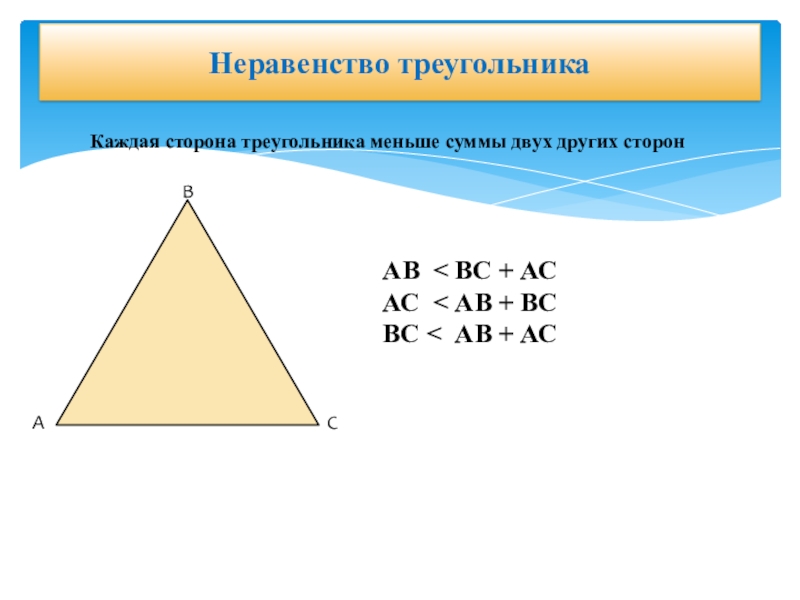
Слайд 15Неравенство треугольника
Каждая сторона треугольника меньше суммы двух других сторон
А
В
С
АВ < ВС
+ АС
АС < АВ + ВС
ВС < АВ + АС
АС < АВ + ВС
ВС < АВ + АС
Слайд 16Сумма углов треугольника равна 180°
A
B
C
смежный с каким-нибудь углом треугольника, называется внешним
О
<АВО – внешний
Слайд 17
<3 = 180°
<1 + <2 = <4
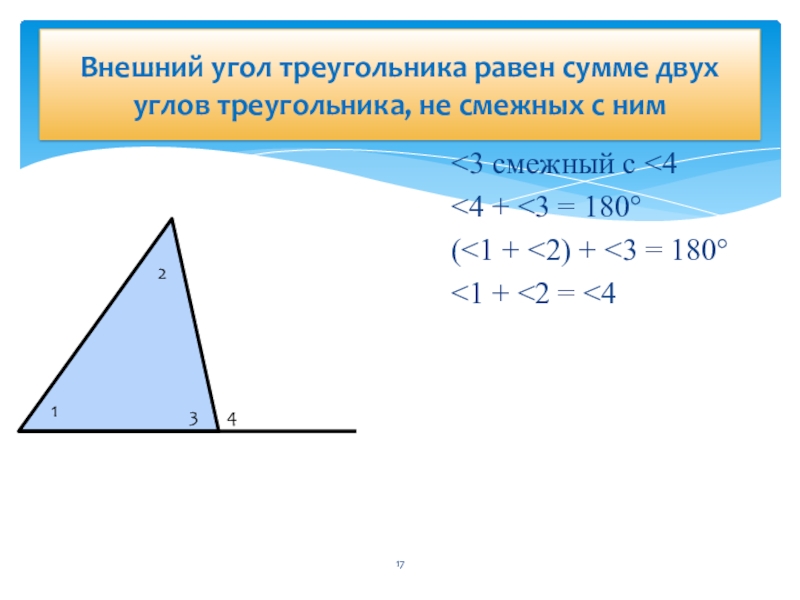
<1 + <2 = <4
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
1
2
3
4
Слайд 18Зависимость между величинами сторон и углов треугольника
В треугольнике:
1) против большей
стороны лежит больший угол;
2) обратно, против большего угла лежит большая сторона
2) обратно, против большего угла лежит большая сторона
1. В прямоугольном треугольнике гипотенуза больше катета
2. Если два треугольника равны, то треугольник равнобедренный
Слайд 19Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько равных
отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки
а
b
А1
А2
А3
А1 А2 = А2А3 = А3 А4
А4
Проведем параллельные прямые
В1
В2
В3
В4
В1В2 = В2В3 = В3В4
Слайд 20Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого
А
С
В
В1
А1
С1
Слайд 21Признаки подобия треугольников
1. Если два угла одного треугольника соответственно равны двум
углам другого треугольника, то такие треугольники подобны
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
А
В
С
К
М
Р
Если Если ∆АВС ∞ ∆КРМ
то ∆АВС ∞ ∆КРМ
АВ : КР = АС : КМ,
<А = <К,
то ∆АВС ∞ ∆КРМ
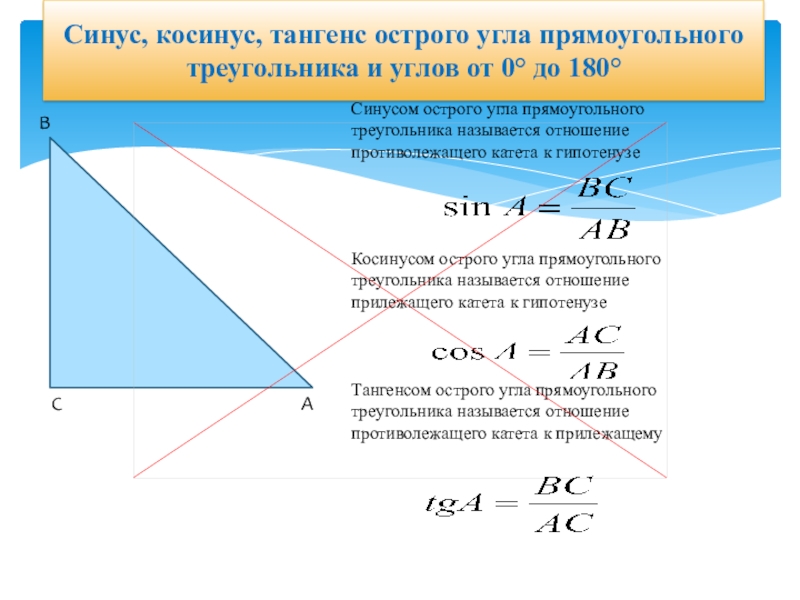
Слайд 22Синус, косинус, тангенс острого угла прямоугольного треугольника и углов от 0°
до 180°
С
А
В
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
Слайд 23sin² x + cos² x = 1
Основное тригонометрическое тождество
Теорема о площади
треугольника
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними
a
b
C
Слайд 25Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними
Теорема косинусов
а
b
c
C
B
A
Слайд 26№ 9. (демонстрационный вариант 2013 г) В равнобедренном треугольнике АВС с основанием
АС внешний угол при вершине С равен 123°. Найдите величину угла АВС. Ответ дайте в градусах.
Решение:
123° А С В
Слайд 29№ 24 (демонстрационный вариант 2013 г) В прямоугольном треугольнике АВС с прямым
углом С известны катеты: АС = 6, ВС = 8. Найдите медиану СК этого треугольника
Решение:
С
В
А
К
Ответ: 5
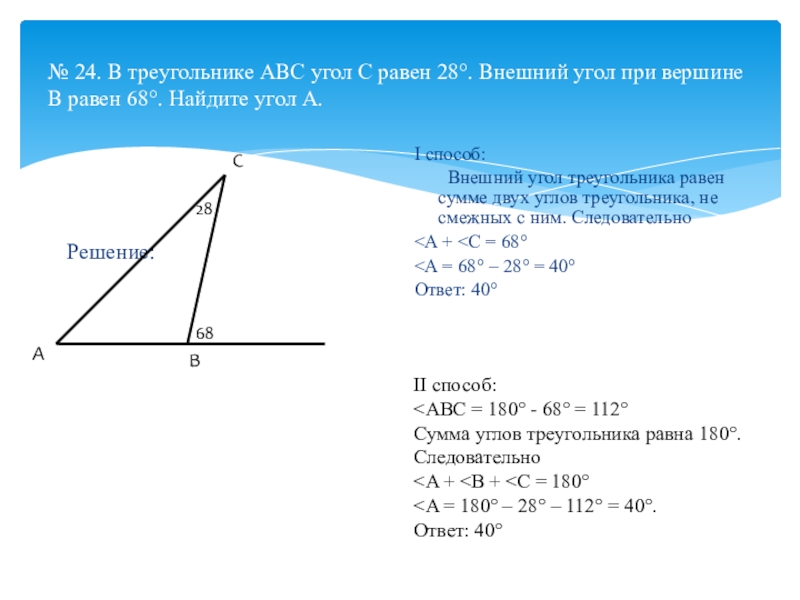
Слайд 30№ 24. В треугольнике АВС угол С равен 28°. Внешний угол
при вершине В равен 68°. Найдите угол А.
Решение:
I способ: А В С 28 68 II способ:
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Следовательно
Ответ: 40°
Следовательно
Ответ: 40°
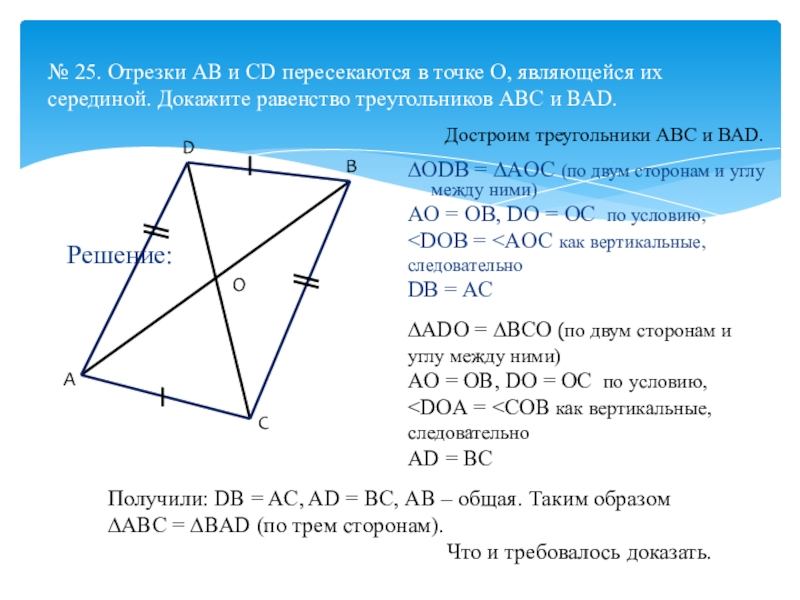
Слайд 31№ 25. Отрезки АВ и CD пересекаются в точке О, являющейся
их серединой. Докажите равенство треугольников АВС и ВАD.
Решение:
∆ODB = ∆AOC (по двум сторонам и углу между ними) А D С В О Достроим треугольники АВС и ВАD. ∆ADO = ∆BCO (по двум сторонам и углу между ними) Получили: DB = AC, AD = BC, АВ – общая. Таким образом
AO = OB, DO = OC по условию,
DB = AC
AO = OB, DO = OC по условию,
АD = ВC
∆ABC = ∆BAD (по трем сторонам).
Что и требовалось доказать.
Слайд 32№25. В треугольнике АВС М – середина АВ, N – середина
ВС. Докажите подобие треугольников MBN и ABC.
Решение:
Так как MN || АС, А В С М N Так как М и N середины сторон АВ и ВС, то MN – средняя линия ∆АВС следовательно MN || АС. следовательно
то
∆MBN ∞ ∆ABC (по двум углам)
Что и требовалось доказать
Слайд 33№ 25. В прямоугольном треугольнике KLM с прямым углом L проведена
высота LP. Докажите, что LP² = KP·MP.
Решение:
∆KLM ∞ ∆KPL по двум углам L M K P Что и требовалось доказать.
(
(
(углы при вершине P прямые,
