- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Золотое сечение
Содержание
- 1. Презентация по математике на тему Золотое сечение
- 2. Цель работы: исследовать наличие « золотого сечения» в архитектуре г. Астаны
- 3. Слайд 3
- 4. Методы исследования: анализ теоретической литературыматематические расчеты пропорциональных
- 5. Понятие золотого сечения.В математике пропорцией (лат. proportio)
- 6. Золотое сечение – это такое пропорциональное деление
- 7. Деление отрезка прямой по золотому сечению. BC
- 8. История развития золотого сечения
- 9. Динамические прямоугольники
- 10. Античный циркуль золотого сечения
- 11. Цейзинг проделал колоссальную работу. Он измерил около
- 12. Ряд чисел 0, 1, 1, 2, 3,
- 13. Примеры архитектурных памятников, построенных по «золотому сечению»
- 14. Гармония – вот что лежит в основе
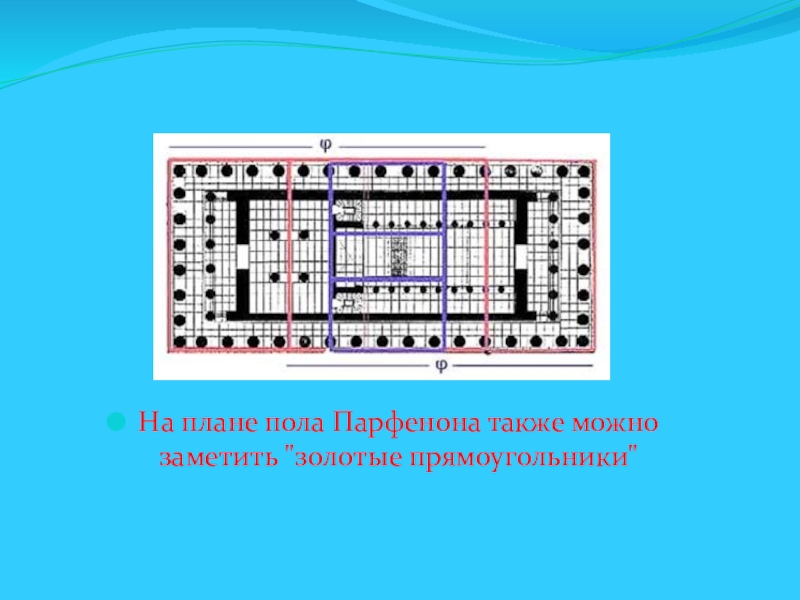
- 15. На плане пола Парфенона также можно заметить "золотые прямоугольники"
- 16. Пропорции пирамиды Хеопса, предметов быта и украшений
- 17. Этот самый большой из всех готических
- 18. Трудно найти человека, который бы не
- 19. Еще один архитектурный шедевр Москвы - дом
- 20. Архитектурные сооружения города Астаны
- 21. 117,525АВСКДом культурыа. БулаксайАВ:ВС=ВС:СК= АB:BK=1,6
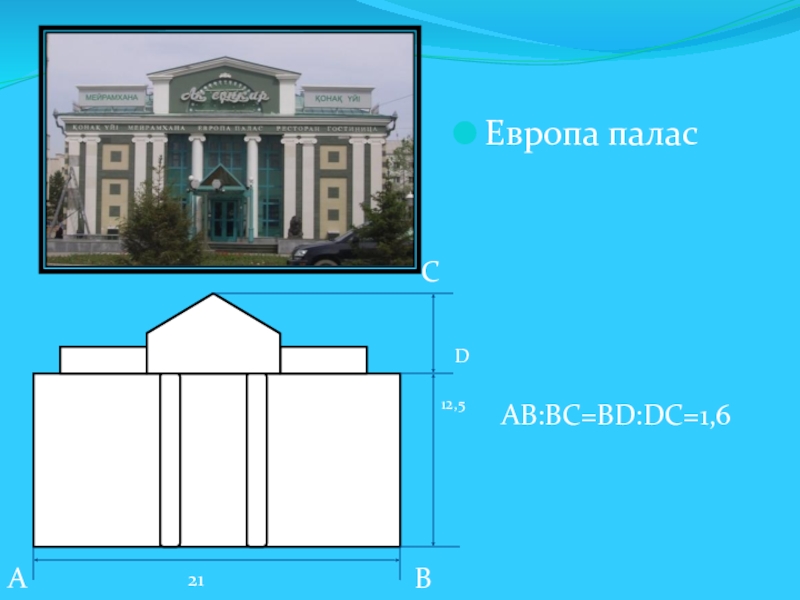
- 22. Европа палас2112,5АВСАВ:ВС=BD:DC=1,6D
- 23. Главпочтамт22,5ВА15САВ:ВС=1,6
- 24. Универмаг «Москва»11,519,5ВАСАВ:ВС=1,6
- 25. Административное здание915,5АВСАВ:ВС=1,6
- 26. Административное здание8,512,5АВСАВ:ВС=0,6
- 27. Мечеть3,86,5АВ:ВС=AD:DB=0,6АВСD
- 28. Правильная пирамида7,57,57,5Дворец мира и согласия
- 29. Ақ Орда115,5АВ:ВС=0,6АВС
- 30. Монумент СлавыАВ:КС=1,669АВСК
- 31. Административное здание на Круглой площади С6,541,52,5АВКДАВ:ВС=ДК:КС=0,6
- 32. Слайд 32
- 33. Спасибо за внимание!
Слайд 3
изучить литературу по теме « Золотое сечение»
подобрать информацию из различных интернет- источников
подготовить коллекцию фотографий с историческими и современными архитектурными зданиями Г. Астаны
провести математические расчеты в вычислении пропорций « золотого сечения»
обобщить полученные результаты
Слайд 4Методы исследования:
анализ теоретической литературы
математические расчеты пропорциональных отношений
составление полученных данных
Объект исследования:
Предмет исследования: отражение « золотого сечения» в архитектуре города
Гипотеза: в архитектуре золотое сечение является основополагающим принципов красоты, прочности, надежности
Слайд 5Понятие золотого сечения.
В математике пропорцией (лат. proportio) называют равенство двух отношений:
a : b = c : d.
Отрезок прямой АВ можно разделить на две части следующими способами:
на две равные части – АВ : АС = АВ : ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Слайд 6Золотое сечение – это такое пропорциональное деление отрезка на неравные части,
a : b = b : c или с : b = b : а.
Геометрическое изображение золотой пропорции.
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
Слайд 7Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
Свойства золотого сечения описываются уравнением:
x2 – x – 1 = 0.
Решение этого уравнения обозначим Ф и оно равно:
≈1,618
Слайд 11Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел
Слайд 12 Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21,
Слайд 14 Гармония – вот что лежит в основе всех видов искусства на
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).
На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618...
Слайд 16Пропорции пирамиды Хеопса, предметов быта и украшений из гробницы Тутанхамона свидетельствуют,
Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Слайд 17 Этот самый большой из всех готических соборов мира вмещает
40
Пропорции это собора являются золотым сечением,
j : j 2 : j 3 : j 4 : j 5 : j 6 : j 7= 0,618
Слайд 18 Трудно найти человека, который бы не знал и не видел
1 : j : j 2 : j 3 : j 4 : j 5 : j 6 : j 7,
где j =0,618