- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Вписанная и описанная окружность(8 класс)
Содержание
- 1. Презентация по математике на тему Вписанная и описанная окружность(8 класс)
- 2. Многоугольник называется описанным около окружности, если все
- 3. Если суммы противоположных сторон четырехугольника равны ,то в него можно вписать окружностьОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИDC+AB=AD+BC
- 4. Многоугольник называется вписанным в окружность, если все
- 5. Если сумма противоположных углов четырехугольника равна 180о,то около него можно описать окружность.ВПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
- 6. ЗАДАЧА 1?H
- 7. 1 способ:
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
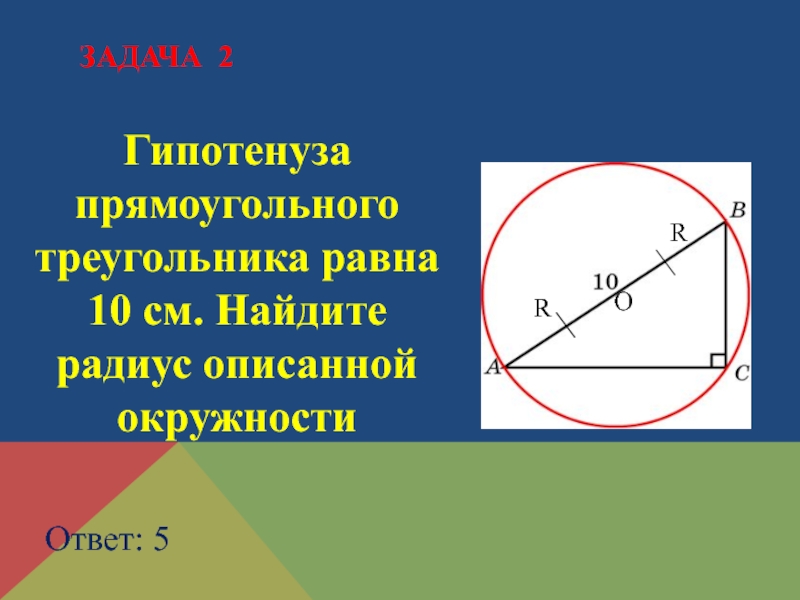
- 11. Гипотенуза прямоугольного треугольника равна 10 см. Найдите радиус описанной окружности Ответ: 5 ЗАДАЧА 2ОRR
- 12. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой сторонеОтвет: 30о ЗАДАЧА 3ORR
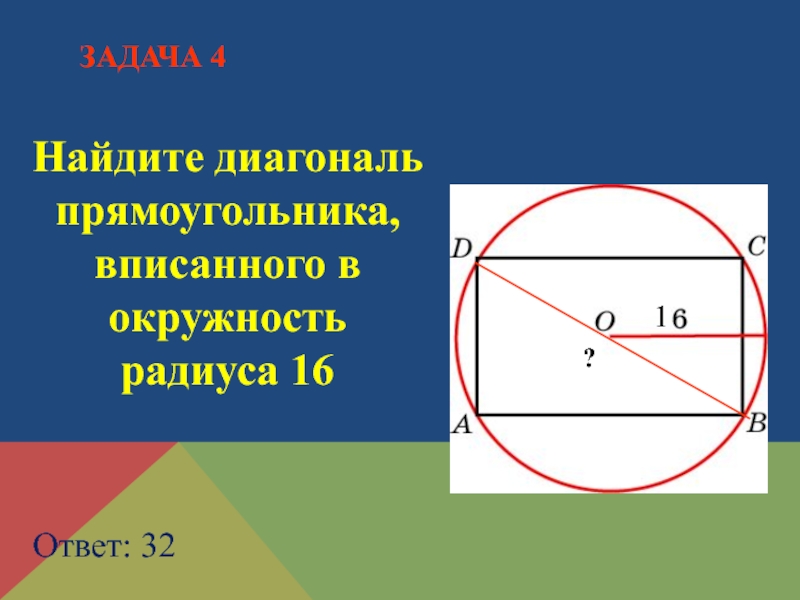
- 13. Найдите диагональ прямоугольника, вписанного в окружность радиуса 16 Ответ: 32 ЗАДАЧА 4?1
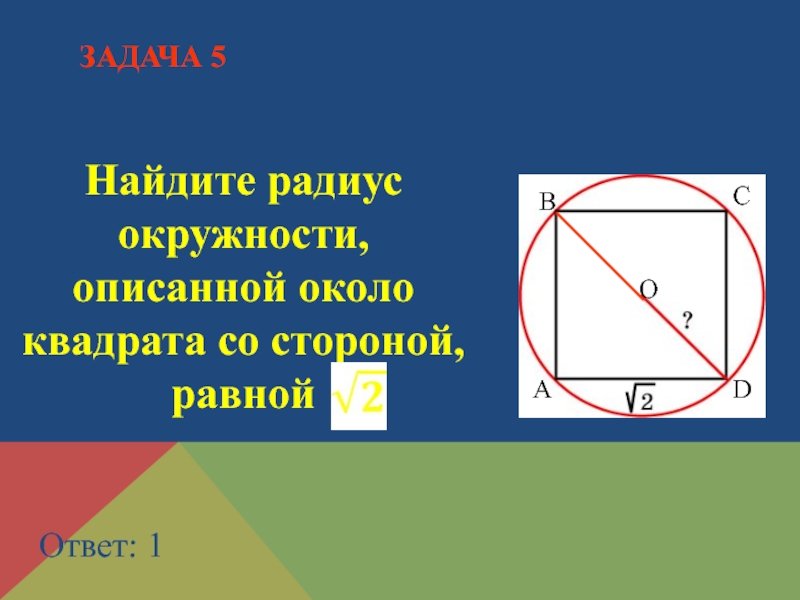
- 14. Найдите радиус окружности, описанной около квадрата со стороной, равной Ответ: 1 ЗАДАЧА 5АВСDO
- 15. Меньшая сторона прямоугольника равна 5 см. Угол
- 16. Около окружности радиуса, равного ,
- 17. Окружность, вписанная в равнобедренный треугольник, делит в
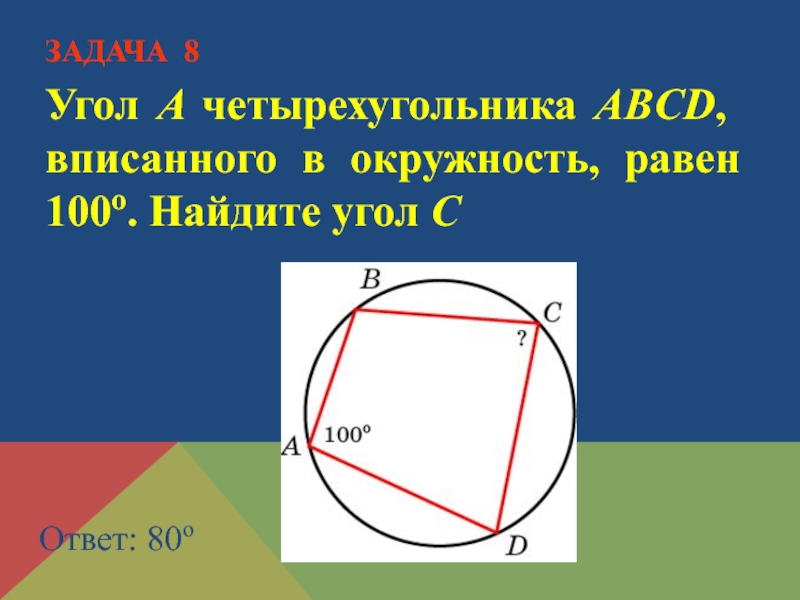
- 18. Угол A четырехугольника ABCD, вписанного в окружность, равен 100о. Найдите угол C Ответ: 80о ЗАДАЧА 8
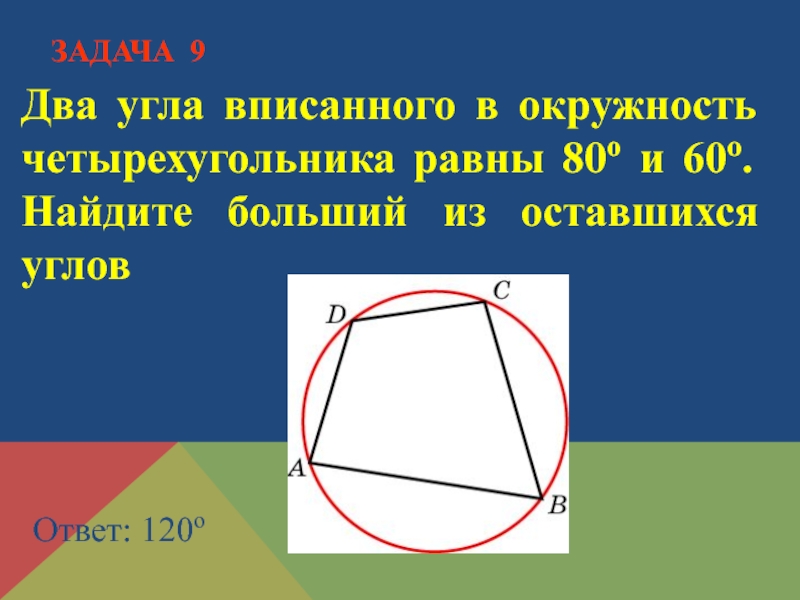
- 19. Два угла вписанного в окружность четырехугольника равны
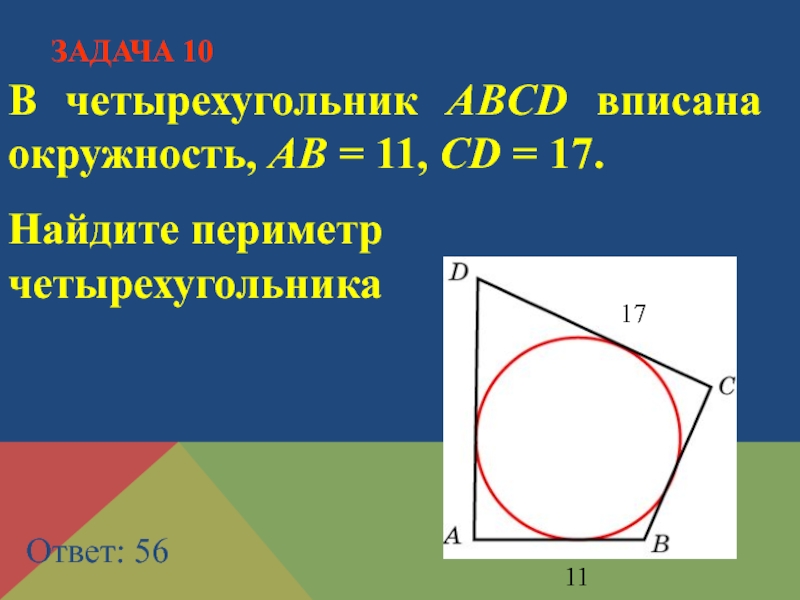
- 20. В четырехугольник ABCD вписана окружность, AB =
- 21. Боковые стороны равнобедренного треугольника равны 40, основание
- 22. СПАСИБО ЗА УРОК!
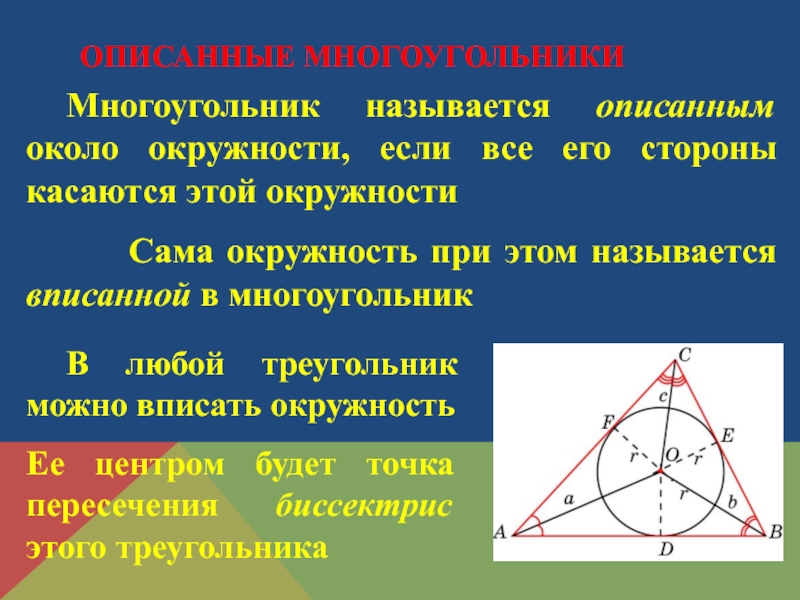
Слайд 2 Многоугольник называется описанным около окружности, если все его стороны касаются этой
Сама окружность при этом называется вписанной в многоугольник
В любой треугольник можно вписать окружность
Ее центром будет точка пересечения биссектрис этого треугольника
ОПИСАННЫЕ МНОГОУГОЛЬНИКИ
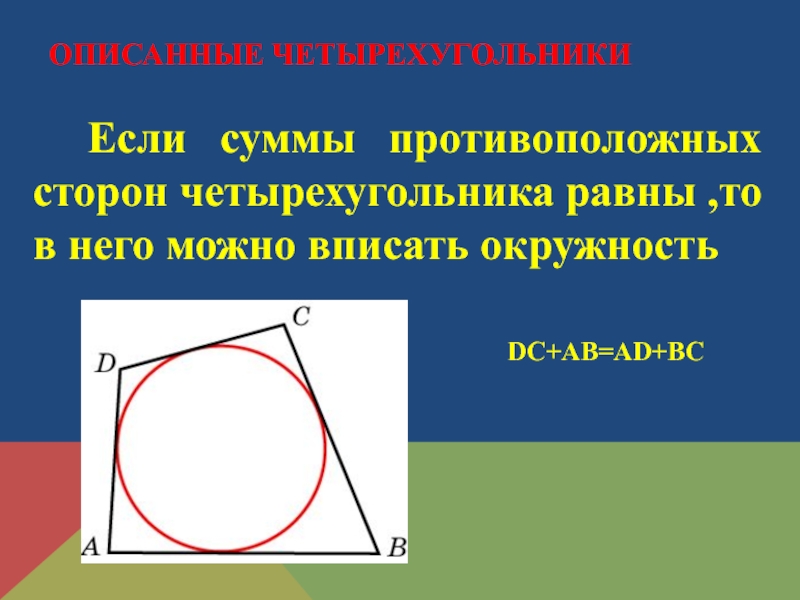
Слайд 3 Если суммы противоположных сторон четырехугольника равны ,то в него можно
ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
DC+AB=AD+BC
Слайд 4 Многоугольник называется вписанным в окружность, если все его вершины принадлежат окружности
Окружность при этом называется описанной около многоугольника
Около любого треугольника можно описать единственную окружность
Ее центром является точка пересечения серединных перпендикуляров к сторонам треугольника
ВПИСАННЫЕ МНОГОУГОЛЬНИКИ
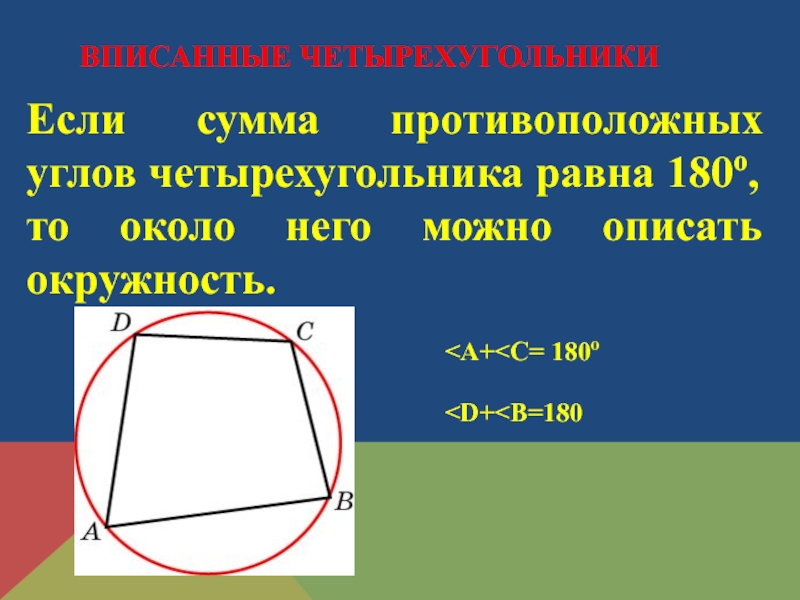
Слайд 5Если сумма противоположных углов четырехугольника равна 180о,то около него можно описать
ВПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
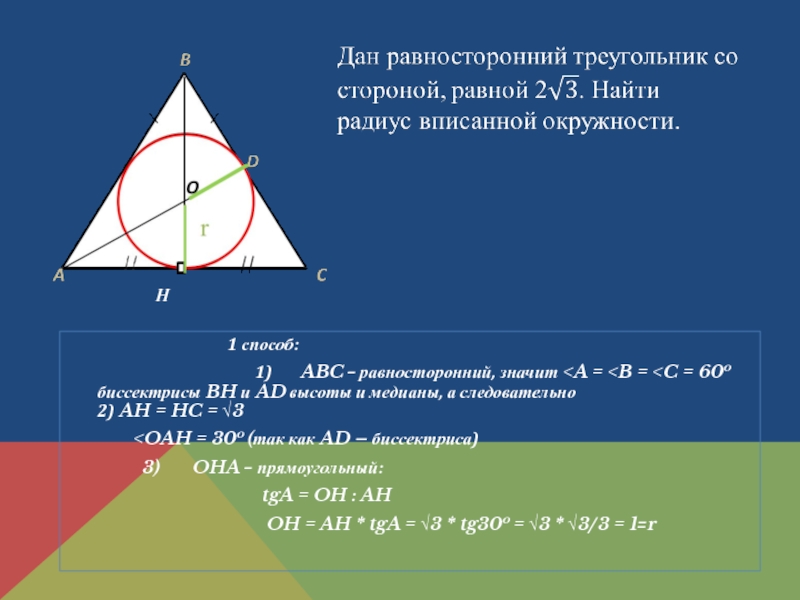
Слайд 7
1 способ:
tgA = OH : AH
OH = AH * tgA = √3 * tg30o = √3 * √3/3 = 1=r
H
Слайд 8
1) Рассмотрим BOD и BHC
1. < B – общий;
2. < BDO =
OD:HC=BD:BH=BO:BC
BD=DC= √3 => OD: √3= √3:BH
BHC – прямоугольный, по теореме Пифагора:
BH2 = BC2 – HC2
BH2 = (2 √ 3) 2 – (√ 3) 2 = 9 => BH = 3
OD: √ 3 = √ 3:3 => OD = √3* √3:3 = 1 = r
H
Слайд 9
1) S р/с = a2 √ 3 /4 S =r*p , где р=1/2Р
S р/с = a2 √ 3 / 4 = ( 2 √ 3) 2 √ 3 : 4 = 4 * 3 √3 / 4 = 3 √3
2) P = AB +BC + AC = 3 AB = 3 * 2 √ 3 = 6 √3
3) p = P / 2 = 6 √ 3 : 2 = 3 √ 3
4) S=r*p r = S / p = 3 √3 /3 √3 = 1
Ответ: 1
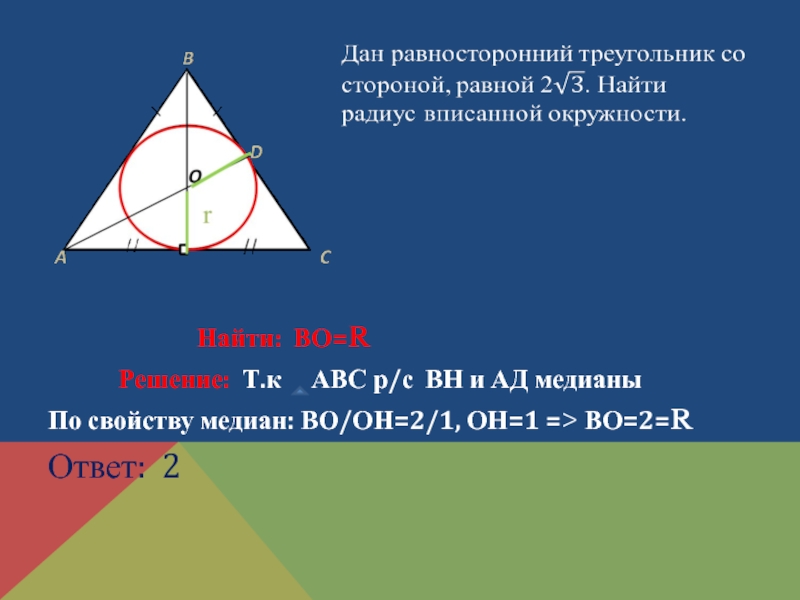
Слайд 10
Решение: Т.к АВС р/с ВН и АД медианы
По свойству медиан: ВО/ОН=2/1, ОН=1 => ВО=2=R
Ответ: 2
Слайд 11Гипотенуза прямоугольного треугольника равна 10 см. Найдите радиус описанной окружности
Ответ: 5
ЗАДАЧА 2
О
R
R
Слайд 12Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий
Ответ: 30о
ЗАДАЧА 3
O
R
R
Слайд 14Найдите радиус окружности, описанной около квадрата со стороной, равной
Ответ: 1
ЗАДАЧА 5
А
В
С
D
O
Слайд 15Меньшая сторона прямоугольника равна 5 см. Угол между диагоналями равен 60о.
Ответ: 15
ЗАДАЧА 5
о
11
Слайд 16Около окружности радиуса, равного , описан квадрат. Найдите радиус
Ответ: 2
ЗАДАЧА 6
2
4
O
√2
Слайд 17Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из
Ответ: 20
ЗАДАЧА 7
H
D
E
3
3
3
4
Слайд 18Угол A четырехугольника ABCD, вписанного в окружность, равен 100о. Найдите угол
Ответ: 80о
ЗАДАЧА 8
Слайд 19Два угла вписанного в окружность четырехугольника равны 80о и 60о. Найдите
Ответ: 120о
ЗАДАЧА 9
Слайд 20В четырехугольник ABCD вписана окружность, AB = 11, CD = 17.
Найдите периметр четырехугольника
Ответ: 56
ЗАДАЧА 10
11
17
Слайд 21Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус
Ответ: 25
ЗАДАЧА 11
0
24