СОШ «Рязанские сады»
Учитель: Ярославцева Л.Е.
2013-2014
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по математике на тему Теорема Пифагора (8 класс)
- 2. Цели проекта. 1. Расширить свои знания по истории
- 3. Задачи проекта.1. Найти исторический материал из биографии
- 4. Введение.«Геометрия владеет двумя сокровищами: одно из них
- 5. История. Пифагор родился около 570
- 6. История теоремы.Измеряй свои желания,взвешивай свои мысли,исчисляй свои
- 7. Древний Вавилон: Несколько больше известно о
- 8. Древняя Индия: Геометрия у индусов,
- 9. Древний Египет: Считается, что равенство:
- 10. Строго говоря, хоть теорема
- 11. Способы доказательств. На данный момент
- 12. Доказательство Басхари «Смотри!» Доказательство великого индийского математика
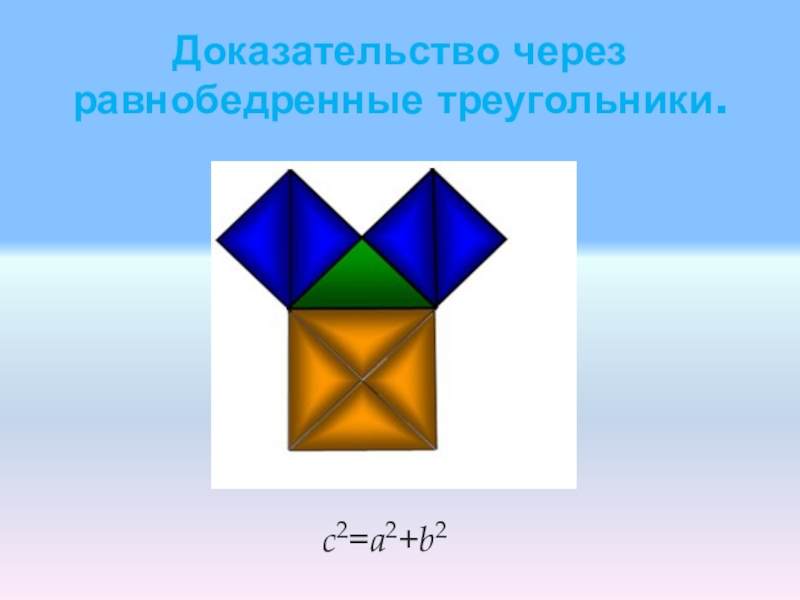
- 13. Доказательство через равнобедренные треугольники. с2=а2+b2
- 14. Дружеские шаржи, которые рисовали ученики пифагорейской школыКстати,
- 15. Доказательство древних индусов. На рисунке
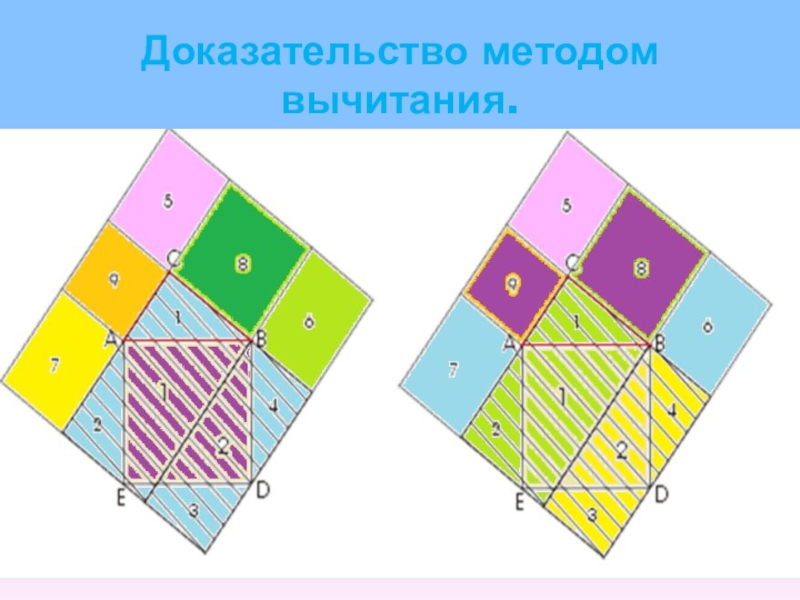
- 16. Доказательство методом вычитания.
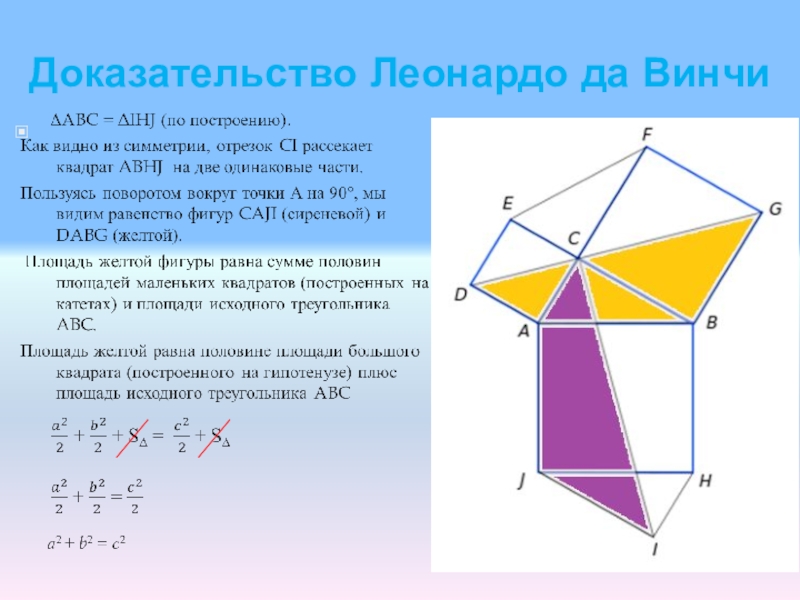
- 17. Доказательство Леонардо да Винчи
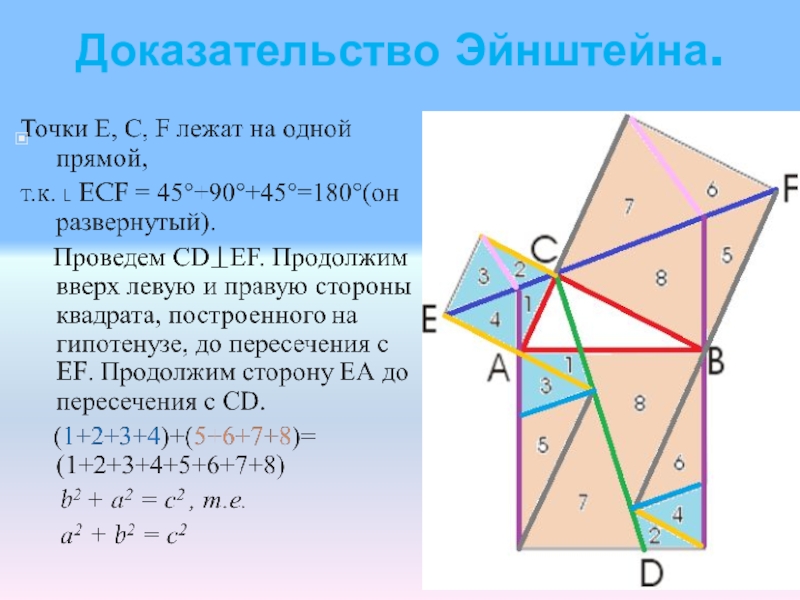
- 18. Доказательство Эйнштейна.
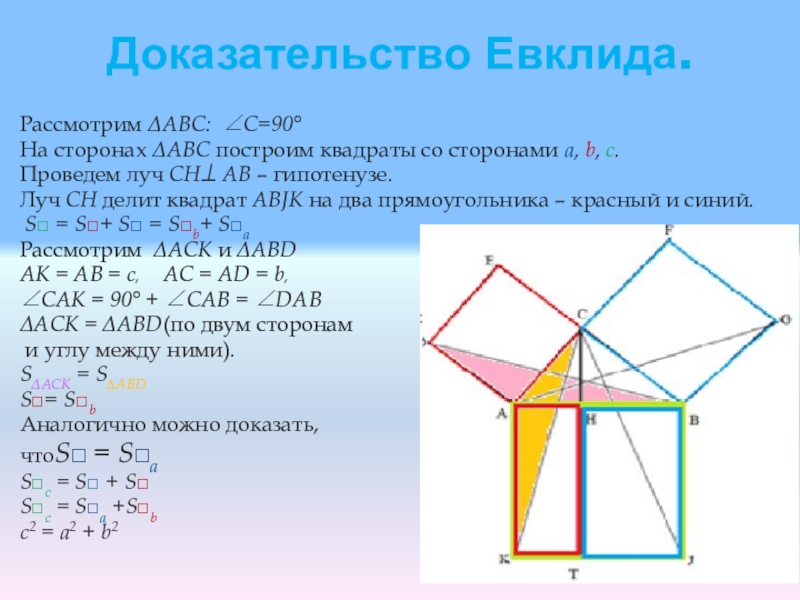
- 19. Доказательство Евклида.Рассмотрим ΔАВС: С=90°На сторонах ΔABC построим
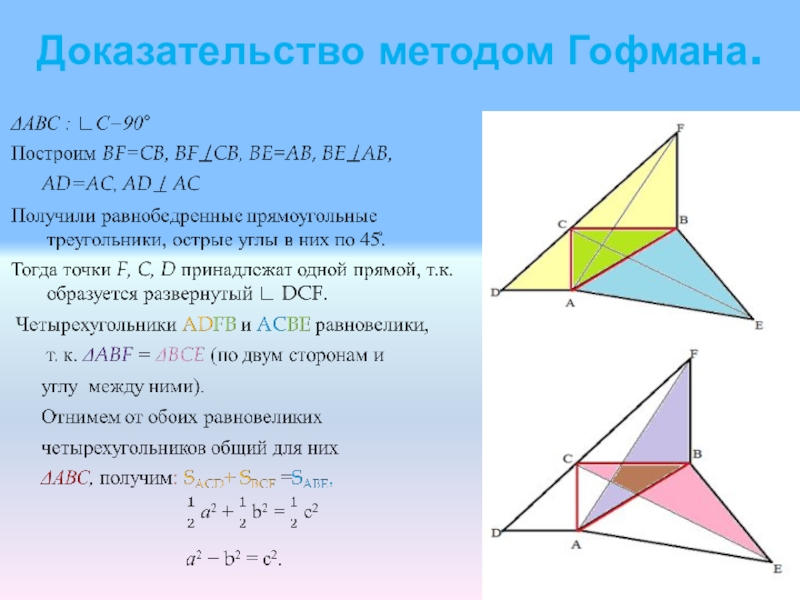
- 20. Доказательство методом Гофмана.
- 21. Доказательство, основанное на разрезании квадратов («Колесо с
- 22. Доказательство по косинусу.
- 23. Теорема Пифагора получила много различных
- 24. Практическое применение. Теорема Пифагора находит
- 25. Задача №1Дано:ΔАВС, ∟С = 90°АС = 8
- 26. Задача 2Дано: ΔАВС, ∟С = 90°АВ =13
- 27. Заключение. Теорема Пифагора –
Цели проекта. 1. Расширить свои знания по истории математики.2. Узнать больше информации, легенд, мифов о Пифагоре и о его теореме.3. Познакомиться с различными способами доказательства теоремы Пифагора.4. Найти ответ на вопрос: «В чем уникальность теоремы Пифагора?»5. Овладеть
Слайд 1Различные способы доказательств теоремы пифагора.
ПРОЕКТ
Ермиловой Екатерины
ученицы 8 класса
МБОУ –
Слайд 2Цели проекта.
1. Расширить свои знания по истории математики.
2. Узнать больше информации,
легенд, мифов о Пифагоре и о его теореме.
3. Познакомиться с различными способами доказательства теоремы Пифагора.
4. Найти ответ на вопрос: «В чем уникальность теоремы Пифагора?»
5. Овладеть навыками применения ИКТ.
3. Познакомиться с различными способами доказательства теоремы Пифагора.
4. Найти ответ на вопрос: «В чем уникальность теоремы Пифагора?»
5. Овладеть навыками применения ИКТ.
Слайд 3Задачи проекта.
1. Найти исторический материал из биографии Пифагора и о его
теореме.
2. Выступить с докладом о Пифагоре перед одноклассниками на кружке «Математический калейдоскоп».
3. Найти и разобрать различные способы доказательства теоремы Пифагора.
4. Рассмотреть применение теоремы Пифагора при решении задач из различных разделов геометрии.
5. Создать презентацию своего проекта.
2. Выступить с докладом о Пифагоре перед одноклассниками на кружке «Математический калейдоскоп».
3. Найти и разобрать различные способы доказательства теоремы Пифагора.
4. Рассмотреть применение теоремы Пифагора при решении задач из различных разделов геометрии.
5. Создать презентацию своего проекта.
Слайд 4Введение.
«Геометрия владеет двумя сокровищами: одно из них — это теорема Пифагора...»
Иоганн
Кеплер.
Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни. О ней писали свои произведения великие писатели всего мира. О ней складывалось множество легенд и мифов. Вокруг теоремы ходит много споров: Кто же ее открыл?
Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни. О ней писали свои произведения великие писатели всего мира. О ней складывалось множество легенд и мифов. Вокруг теоремы ходит много споров: Кто же ее открыл?
Слайд 5История.
Пифагор родился около 570 г. до н.э. на
острове Самосе. Отцом Пифагора был
Мнесарх, мать – Парфениса. Будущий
великий математик и философ уже в детстве
обнаружил большие способности к наукам.
У своего первого учителя Гермодамаса Пифагор получает знания основ музыки и живописи. Затем Пифагора отправляется в Милет, где встречается с Фалесом. Затем отправляется в путешествие и попадает в плен к вавилонскому царю Киру. В 530 г. до н.э. Пифагор сбежал на родину.
А на Самосе в то время царствовал тиран Поликрат. Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена ("пифагорейцы"), члены которого обязывались вести так называемый пифагорейский образ жизни.
Слайд 6История теоремы.
Измеряй свои желания,
взвешивай свои мысли,
исчисляй свои слова.
Пифагор
Древний Китай:
В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:
«Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
«Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Слайд 7Древний Вавилон:
Несколько больше известно о теореме Пифагора у вавилонян.
В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э., приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях.
Слайд 8
Древняя Индия:
Геометрия у индусов, была тесно связана с
культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
Слайд 9Древний Египет:
Считается, что равенство: 3² + 4² = 5² было известно уже
египтянам еще около 2300 г. до н. э. По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Слайд 10 Строго говоря, хоть теорема и называется «теоремой Пифагора»,
сам Пифагор ее не открывал. Прямоугольный треугольник и его особенные свойства изучались задолго до него. Есть две полярных точки зрения на этот вопрос. По одной версии Пифагор первым нашел полноценное доказательство теоремы. По другой доказательство не принадлежит авторству Пифагора.
Сегодня уже не проверишь, кто прав, а кто заблуждается. Известно лишь, что доказательства Пифагора, если оно когда-либо существовало, не сохранилось. Впрочем, высказываются предположения, что знаменитое доказательство из «Начал» Евклида может принадлежать как раз Пифагору, и Евклид его только зафиксировал. Однако существует легенда, что когда Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков.
Сегодня уже не проверишь, кто прав, а кто заблуждается. Известно лишь, что доказательства Пифагора, если оно когда-либо существовало, не сохранилось. Впрочем, высказываются предположения, что знаменитое доказательство из «Начал» Евклида может принадлежать как раз Пифагору, и Евклид его только зафиксировал. Однако существует легенда, что когда Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков.
Слайд 11Способы доказательств.
На данный момент в научной литературе зафиксировано
367 доказательств данной теоремы, она занесена в книгу рекордов Гиннеса. Самые известные методы доказательства: методом площадей, аксиоматические и экзотические доказательства.
Я рассмотрела несколько основных приемов доказательства теоремы Пифагора:
1. Алгебраический метод.
2. Метод площадей.
3. Подобие треугольников.
4.Тригонометрический.
Я рассмотрела несколько основных приемов доказательства теоремы Пифагора:
1. Алгебраический метод.
2. Метод площадей.
3. Подобие треугольников.
4.Тригонометрический.
Слайд 12Доказательство Басхари «Смотри!»
Доказательство великого индийского математика Басхари сопровождало лишь одно
слово: СМОТРИ!
Внутри – квадрат со стороной b–a.
(b – a)2 = c2 – 4· 0.5 ab
b2 - 2ab + a2 = c2 – 2ab
b2 + a2 = c2
Внутри – квадрат со стороной b–a.
(b – a)2 = c2 – 4· 0.5 ab
b2 - 2ab + a2 = c2 – 2ab
b2 + a2 = c2
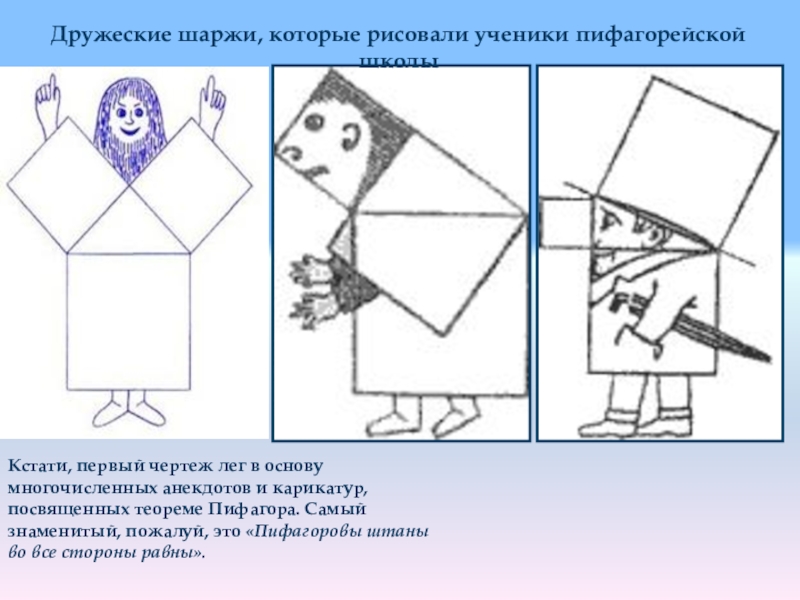
Слайд 14Дружеские шаржи, которые рисовали ученики пифагорейской школы
Кстати, первый чертеж лег в
основу многочисленных анекдотов и карикатур, посвященных теореме Пифагора. Самый знаменитый, пожалуй, это «Пифагоровы штаны во все стороны равны».
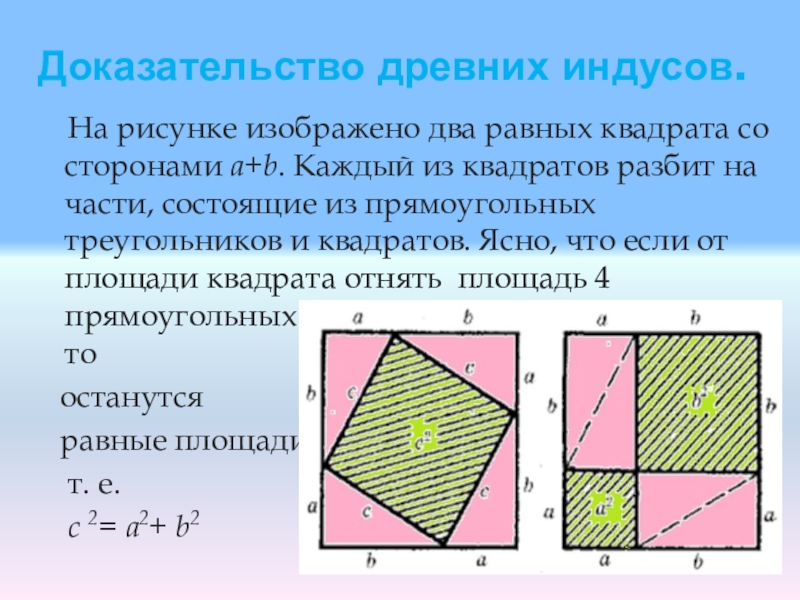
Слайд 15Доказательство древних индусов.
На рисунке изображено два равных квадрата
со сторонами а+b. Каждый из квадратов разбит на части, состоящие из прямоугольных треугольников и квадратов. Ясно, что если от площади квадрата отнять площадь 4 прямоугольных треугольников с катетами a и b, то
останутся
равные площади,
т. е.
с 2= а2+ b2
останутся
равные площади,
т. е.
с 2= а2+ b2
Слайд 19Доказательство Евклида.
Рассмотрим ΔАВС: С=90°
На сторонах ΔABC построим квадраты со сторонами а,
b, с.
Проведем луч СН⟘ АВ – гипотенузе.
Луч СН делит квадрат ABJK на два прямоугольника – красный и синий.
S□ = S□+ S□ = S□b+ S□а
Рассмотрим ΔACK и ΔABD
AK = AB = c, AC = AD = b,
CAK = 90° + CAB = DAB
ΔACK = ΔABD(по двум сторонам
и углу между ними).
SΔACK = S∆ABD
S□= S□b
Аналогично можно доказать,
чтоS□ = S□a
S□c = S□ + S□
S□c = S□a +S□b
с2 = a2 + b2
Проведем луч СН⟘ АВ – гипотенузе.
Луч СН делит квадрат ABJK на два прямоугольника – красный и синий.
S□ = S□+ S□ = S□b+ S□а
Рассмотрим ΔACK и ΔABD
AK = AB = c, AC = AD = b,
CAK = 90° + CAB = DAB
ΔACK = ΔABD(по двум сторонам
и углу между ними).
SΔACK = S∆ABD
S□= S□b
Аналогично можно доказать,
чтоS□ = S□a
S□c = S□ + S□
S□c = S□a +S□b
с2 = a2 + b2
Слайд 21Доказательство, основанное на разрезании квадратов («Колесо с лопастями» - Перигаль)
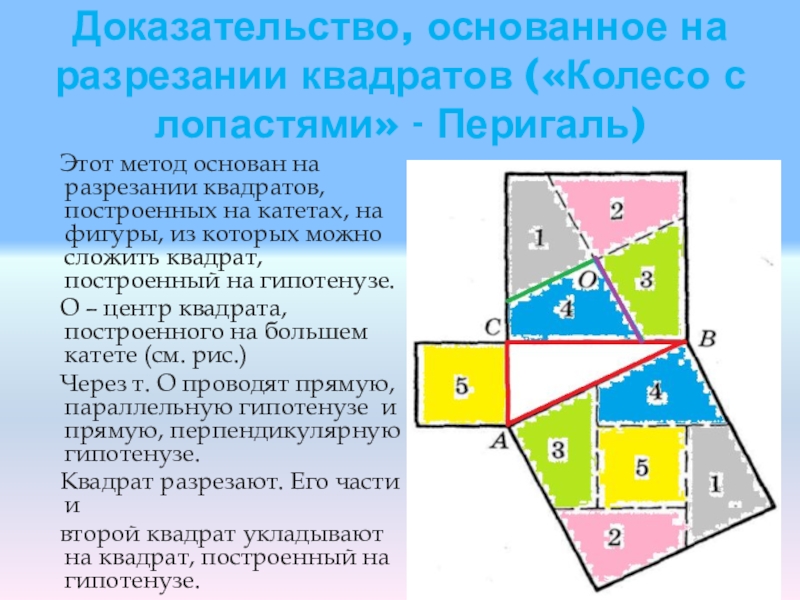
Этот метод основан на разрезании квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.
О – центр квадрата, построенного на большем катете (см. рис.)
Через т. О проводят прямую, параллельную гипотенузе и прямую, перпендикулярную гипотенузе.
Квадрат разрезают. Его части и
второй квадрат укладывают на квадрат, построенный на гипотенузе.
О – центр квадрата, построенного на большем катете (см. рис.)
Через т. О проводят прямую, параллельную гипотенузе и прямую, перпендикулярную гипотенузе.
Квадрат разрезают. Его части и
второй квадрат укладывают на квадрат, построенный на гипотенузе.
Слайд 23 Теорема Пифагора получила много различных названий:
«теорема бабочки»,
«теорема
невесты»,
теорема «100 быков»,
«бегство убогих»,
«ветреная мельница»,
«мост ослов».
Думаю, только по количеству названий, теорему можно считать уникальной!
теорема «100 быков»,
«бегство убогих»,
«ветреная мельница»,
«мост ослов».
Думаю, только по количеству названий, теорему можно считать уникальной!
Слайд 24Практическое применение.
Теорема Пифагора находит применение не только в
математике, но и в астрономии и даже литературе. В математике теорему используют для решения задач, для доказательства других теорем. Что касается литературы, то теорема Пифагора вдохновляла. А в двадцатом веке советский писатель Евгений Велтистов в книге «Приключения Электроника» доказательствам теоремы Пифагора отвел целую главу. Она помогает выйти за границы привычного, и на знакомые вещи посмотреть по-новому.
Слайд 25Задача №1
Дано:
ΔАВС, ∟С = 90°
АС = 8 см
ВС = 6 см
Найти:
АВ
Решение:
а2 + b2 = с2
ВС2 + АС2 = АВ2
62 + 82 = АВ2
36 + 64 = АВ2
АВ2 = 100
АВ = 10 см
Ответ: 10 см.
Решение:
а2 + b2 = с2
ВС2 + АС2 = АВ2
62 + 82 = АВ2
36 + 64 = АВ2
АВ2 = 100
АВ = 10 см
Ответ: 10 см.
Слайд 26Задача 2
Дано: ΔАВС, ∟С = 90°
АВ =13 см
ВС = 12 см
Найти:
АС
Решение:
а2 + b2 = с2
ВС2 + АС2 = АВ2
122 +АС2 = 132
144 +АС2 = 169
АС2 = 25
АС = 5
Ответ: АС = 5 см.
Решение:
а2 + b2 = с2
ВС2 + АС2 = АВ2
122 +АС2 = 132
144 +АС2 = 169
АС2 = 25
АС = 5
Ответ: АС = 5 см.
Слайд 27Заключение.
Теорема Пифагора – одна из главных теорем
в геометрии. Значение ее в том, что с ее помощью можно вывести большинство теорем геометрии. Она замечательна еще тем, что сама по себе она вовсе не является очевидной: сколько ни смотри на прямоугольный треугольник, никак не увидишь, что квадрат гипотенузы равен сумме квадратов катетов. Теорема Пифагора популярна по трем причинам:
1. простота;
2. красота;
3. значимость.
Вот почему теорему Пифагора считают уникальной.
Используемые источники:
http://ru.wikipedia.org/
http://rpp.nashaucheba.ru/
1. простота;
2. красота;
3. значимость.
Вот почему теорему Пифагора считают уникальной.
Используемые источники:
http://ru.wikipedia.org/
http://rpp.nashaucheba.ru/