- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение задач №14 из ЕГЭ №2
Содержание
- 1. Презентация по математике на тему Решение задач №14 из ЕГЭ №2
- 2. Разбор задачи №14Каррыев Эркин
- 3. Условие:В правильной треугольной пирамиде SABC с вершиной S, все рёбра
- 4. Слайд 4
- 5. Слайд 5
- 6. Проектная работа задача №14(ЕГЭ)Подготовил Мехтиев Самир 11 А
- 7. Задача.Дано:Правильная шестиугольная пирамида SABCDEFРебро SA = 2Основание
- 8. Решение.Построим пирамиду в стереометрии и её основание в планиметрии SBCDEFAOABCDEFKKpp
- 9. Решение. 1)В правильной пирамиде основанием высоты является
- 10. Решение. SBCDEFAOKp
- 11. Котцова Лидия 11 АРешение задачи № 14 (ЕГЭ профиль)
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Задача № 14 Мардонова Сабина ученица 11 «А»
- 18. Условие
- 19. Дано:ЦилиндрLS=NF=26LN=FS=21AB=24CD=10KT=√730а) Докажите, что эта плоскость пересекает ось цилиндра.б) найти угол (ABCD; )
- 20. а) Т. к. диаметр равен 26, то
- 21. б) Угол (ABCD; )= углу (TKT1)Рассмотрим ∆КTT1,
- 22. Геометрия. Задание №14 ЕГЭСедова Кристина 11 «А»
- 23. Основание прямой четырехугольной призмы ABCDA1B1C1D1-прямоугольник ABCD, в
- 24. O Дано:ABCDA1B1C1D1 –
- 25. Решение:а) Искомая линия пересечения – перпендикуляр DH,
- 26. Решение:б) АС и B1D1 лежат в параллельных
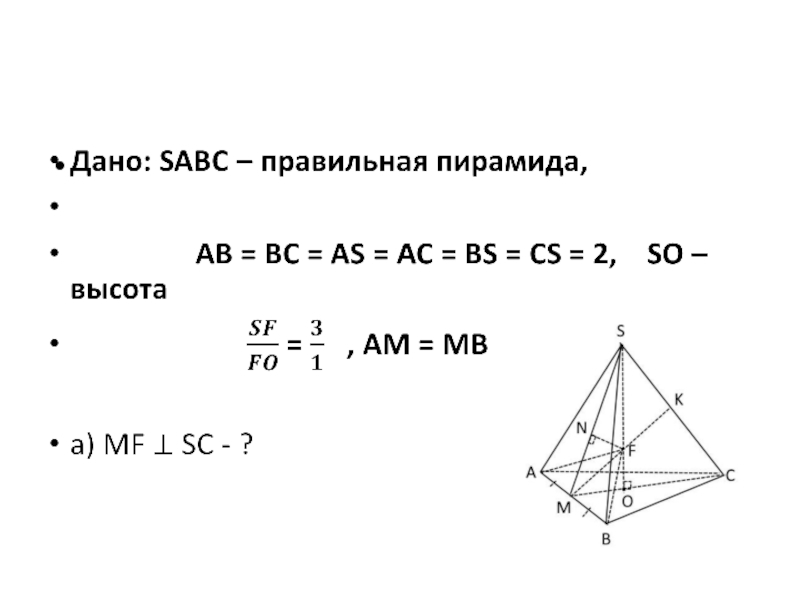
Разбор задачи №14Каррыев Эркин
Слайд 3Условие:
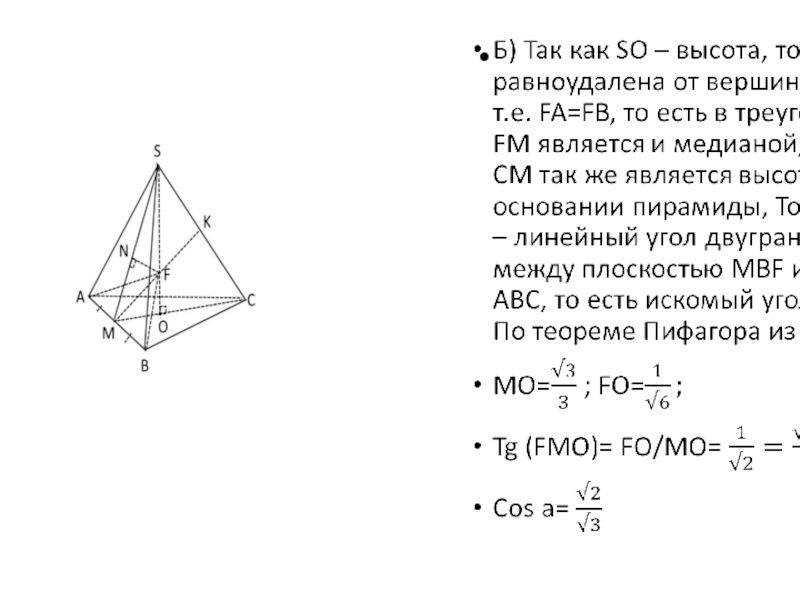
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 2, точка M —
середина ребра AB, точка O — центр основания пирамиды, точка F делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
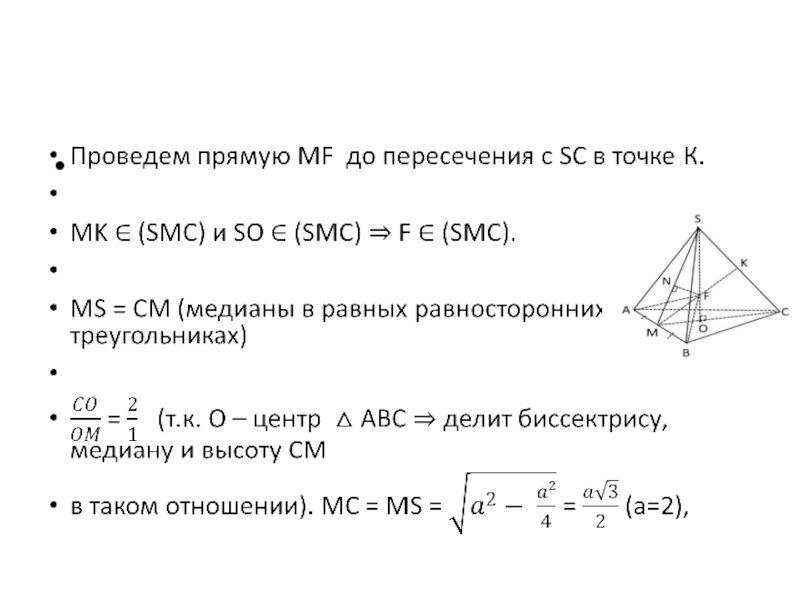
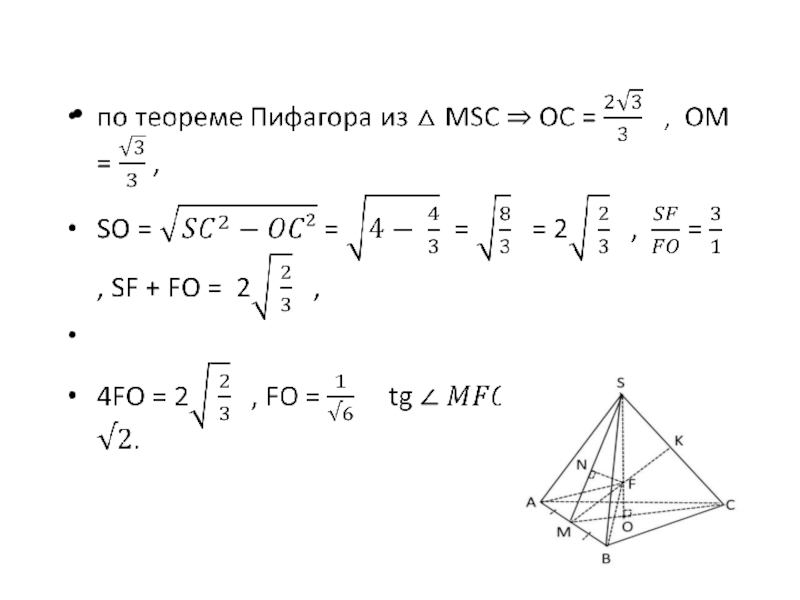
а) Докажите, что прямая MF перпендикулярна прямой SC.
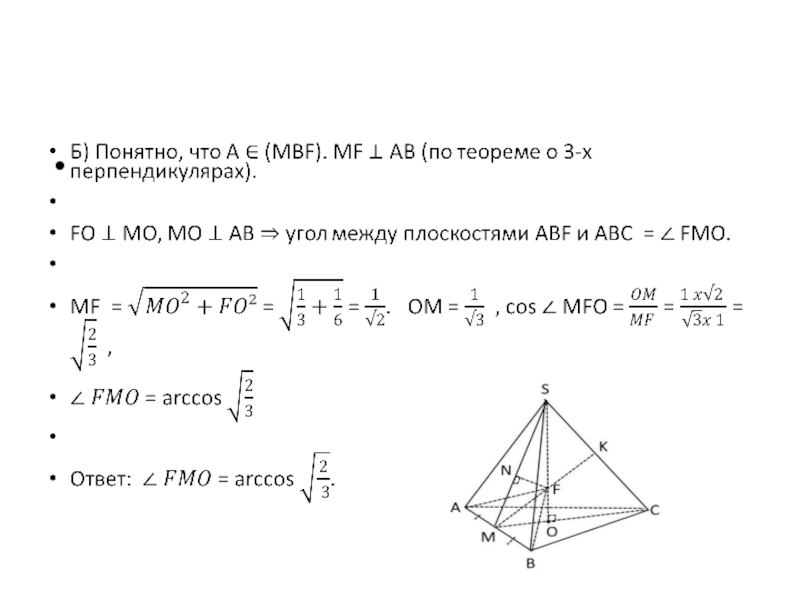
б) Найдите угол между плоскостью MBF и плоскостью ABC.
а) Докажите, что прямая MF перпендикулярна прямой SC.
б) Найдите угол между плоскостью MBF и плоскостью ABC.
Слайд 7Задача.
Дано:
Правильная шестиугольная пирамида SABCDEF
Ребро SA = 2
Основание AF = 1
____________________
1. Доказать,
что плоскость, проходящая через вершину S и середины AF и CD, перпендикулярна плоскости основания.
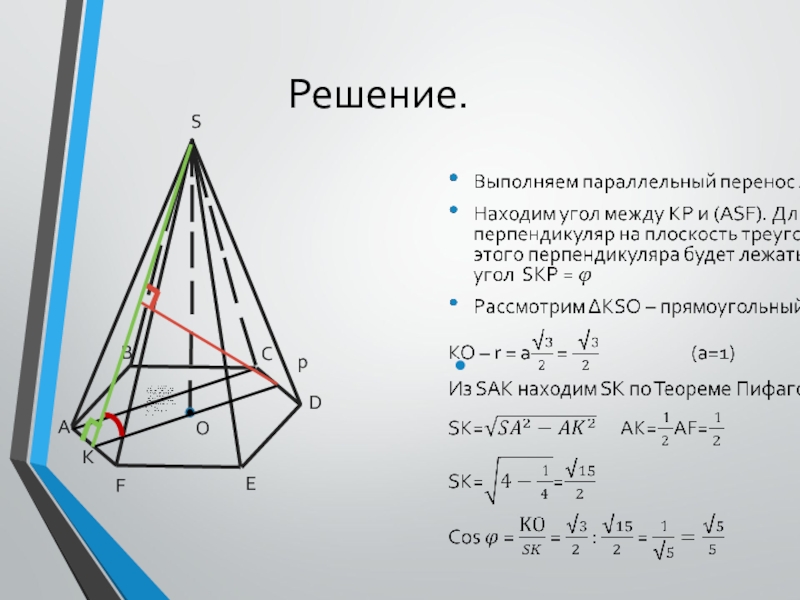
2. Найти косинус угла между прямой AC и плоскостью SAF.
2. Найти косинус угла между прямой AC и плоскостью SAF.
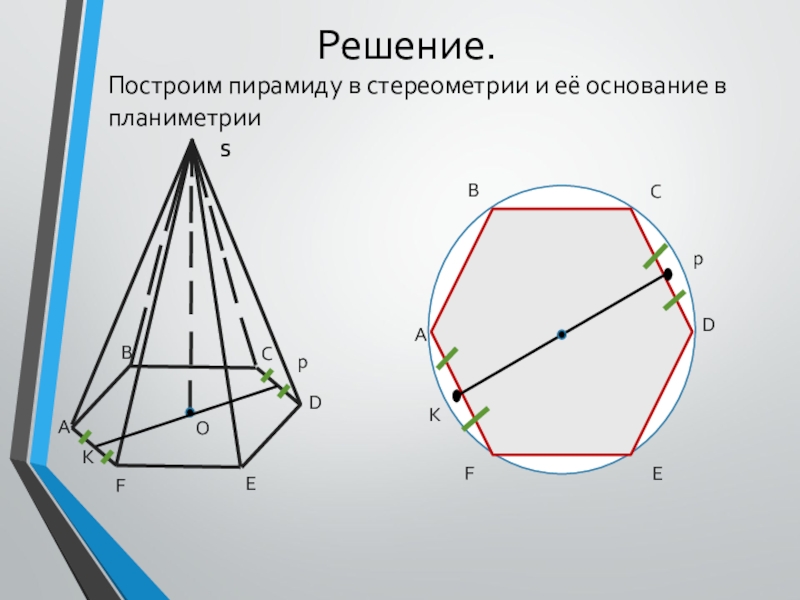
Слайд 9Решение.
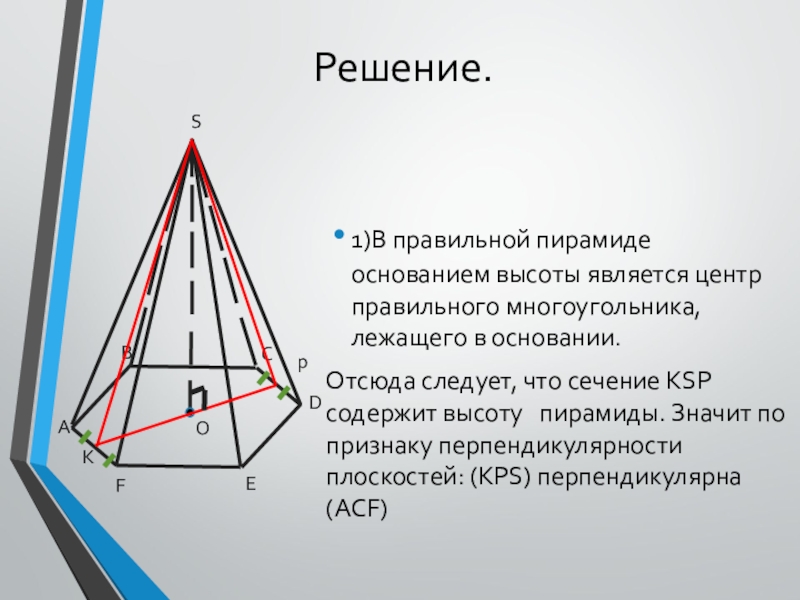
1)В правильной пирамиде основанием высоты является центр правильного многоугольника, лежащего
в основании.
Отсюда следует, что сечение KSP содержит высоту пирамиды. Значит по признаку перпендикулярности плоскостей: (KPS) перпендикулярна (ACF)
Отсюда следует, что сечение KSP содержит высоту пирамиды. Значит по признаку перпендикулярности плоскостей: (KPS) перпендикулярна (ACF)
S
B
C
D
E
F
A
O
K
p
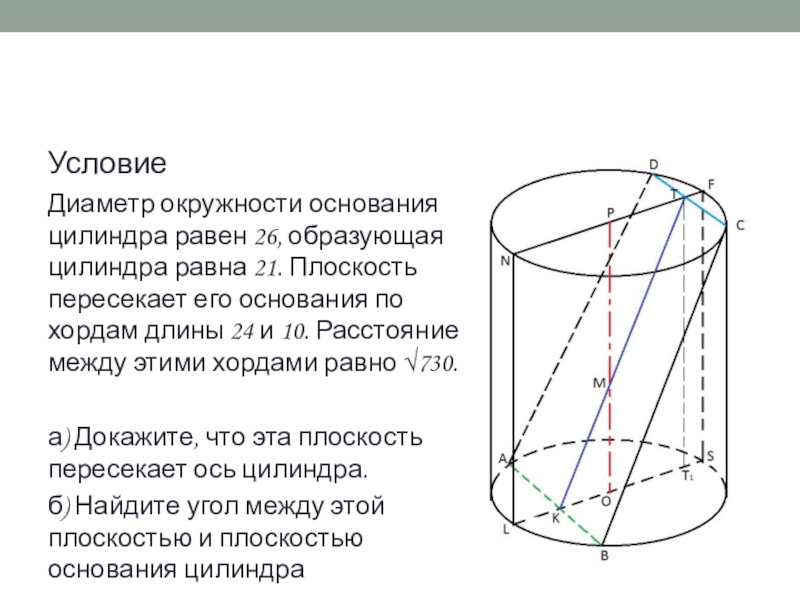
Слайд 18Условие
Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно √730.
а) Докажите, что эта плоскость пересекает ось цилиндра.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра
Слайд 19Дано:
Цилиндр
LS=NF=26
LN=FS=21
AB=24
CD=10
KT=√730
а) Докажите, что эта плоскость пересекает ось цилиндра.
б) найти угол (ABCD;
)
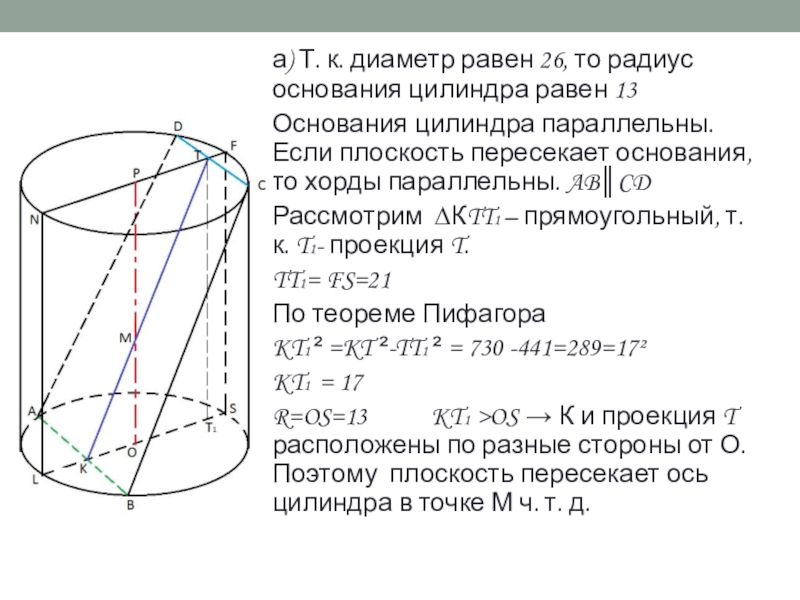
Слайд 20а) Т. к. диаметр равен 26, то радиус основания цилиндра равен
13
Основания цилиндра параллельны. Если плоскость пересекает основания, то хорды параллельны. AB║CD
Рассмотрим ∆КTT1 – прямоугольный, т. к. T1- проекция T.
TT1= FS=21
По теореме Пифагора
KT1 ² =KT ²-TT1 ² = 730 -441=289=17²
KT1 = 17
R=OS=13 KT1 >OS → К и проекция T расположены по разные стороны от О. Поэтому плоскость пересекает ось цилиндра в точке М ч. т. д.
Основания цилиндра параллельны. Если плоскость пересекает основания, то хорды параллельны. AB║CD
Рассмотрим ∆КTT1 – прямоугольный, т. к. T1- проекция T.
TT1= FS=21
По теореме Пифагора
KT1 ² =KT ²-TT1 ² = 730 -441=289=17²
KT1 = 17
R=OS=13 KT1 >OS → К и проекция T расположены по разные стороны от О. Поэтому плоскость пересекает ось цилиндра в точке М ч. т. д.
Слайд 21б) Угол (ABCD; )= углу (TKT1)
Рассмотрим ∆КTT1, где KT1 = 17
и TT1=21
Тогда, tg(TKT1)= TT1 / KT1 =21/17
→ Угол (ABCD; )= arctg (21/17)
Ответ: arctg (21/17)
Тогда, tg(TKT1)= TT1 / KT1 =21/17
→ Угол (ABCD; )= arctg (21/17)
Ответ: arctg (21/17)
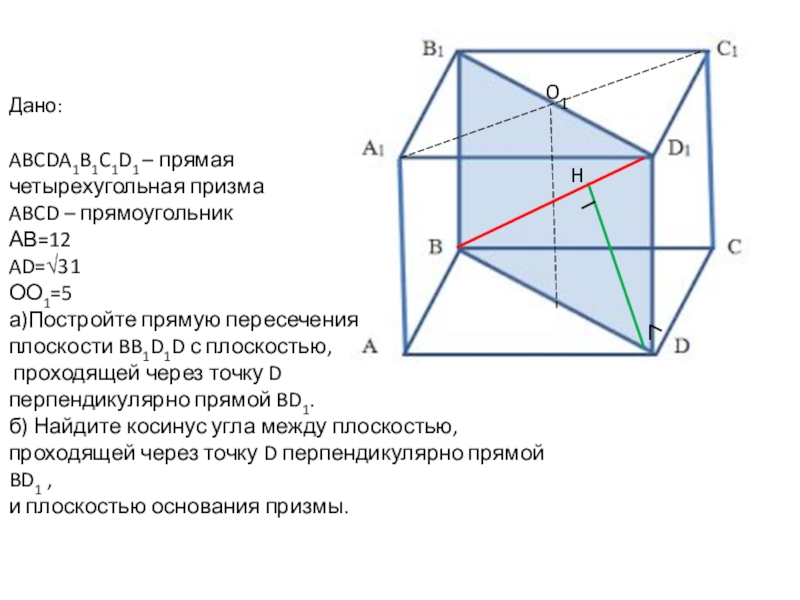
Слайд 23Основание прямой четырехугольной призмы ABCDA1B1C1D1-прямоугольник ABCD, в котором АВ=12, AD=√31. Расстояние
между прямыми АС и В1D1 равно 5.
а)Постройте прямую пересечения плоскости BB1D1D с плоскостью, проходящей через точку D перпендикулярно прямой BD1.
б) Найдите косинус угла между плоскостью, проходящей через точку D перпендикулярно прямой BD1 , и плоскостью основания призмы.
Слайд 24
O
Дано:
ABCDA1B1C1D1 – прямая
четырехугольная призма
ABCD – прямоугольник
АВ=12
AD=√31
ОО1=5
а)Постройте прямую пересечения
плоскости BB1D1D с плоскостью,
проходящей через точку D
перпендикулярно прямой BD1. б) Найдите косинус угла между плоскостью,
проходящей через точку D перпендикулярно прямой BD1 ,
и плоскостью основания призмы.
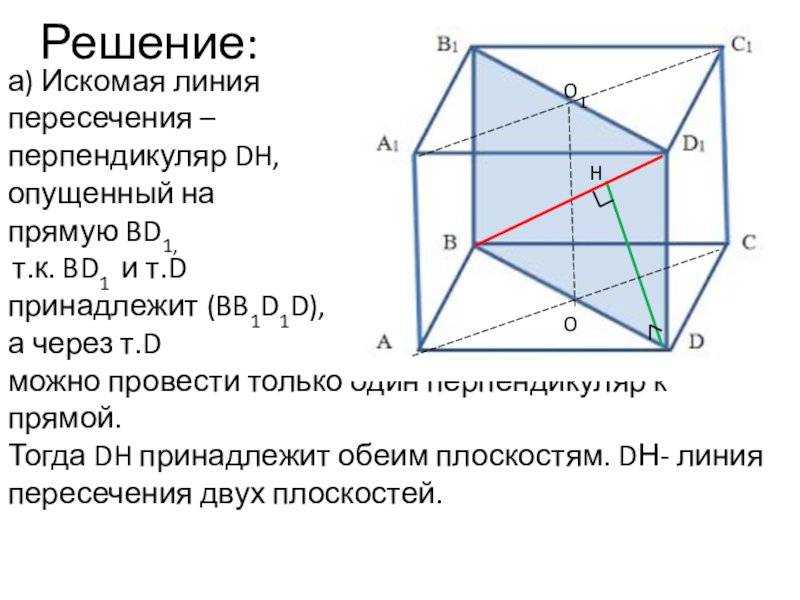
Слайд 25Решение:
а) Искомая линия
пересечения –
перпендикуляр DH,
опущенный на
прямую BD1,
т.к. BD1 и т.D
принадлежит (BB1D1D),
а через т.D
можно провести только один перпендикуляр к прямой.
Тогда DH принадлежит обеим плоскостям. DН- линия пересечения двух плоскостей.
принадлежит (BB1D1D),
а через т.D
можно провести только один перпендикуляр к прямой.
Тогда DH принадлежит обеим плоскостям. DН- линия пересечения двух плоскостей.
H
O1
O
Слайд 26Решение:
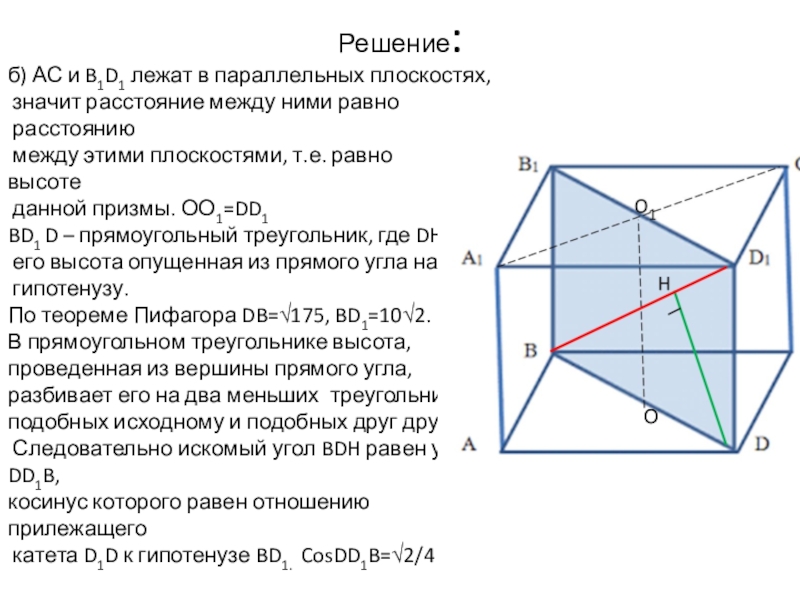
б) АС и B1D1 лежат в параллельных плоскостях,
значит расстояние между
ними равно
расстоянию
между этими плоскостями, т.е. равно
высоте
данной призмы. ОО1=DD1
BD1 D – прямоугольный треугольник, где DH –
его высота опущенная из прямого угла на
гипотенузу.
По теореме Пифагора DB=√175, BD1=10√2.
В прямоугольном треугольнике высота,
проведенная из вершины прямого угла,
разбивает его на два меньших треугольника,
подобных исходному и подобных друг другу.
Следовательно искомый угол BDH равен углу DD1B,
косинус которого равен отношению прилежащего
катета D1D к гипотенузе BD1. CosDD1B=√2/4
расстоянию
между этими плоскостями, т.е. равно
высоте
данной призмы. ОО1=DD1
BD1 D – прямоугольный треугольник, где DH –
его высота опущенная из прямого угла на
гипотенузу.
По теореме Пифагора DB=√175, BD1=10√2.
В прямоугольном треугольнике высота,
проведенная из вершины прямого угла,
разбивает его на два меньших треугольника,
подобных исходному и подобных друг другу.
Следовательно искомый угол BDH равен углу DD1B,
косинус которого равен отношению прилежащего
катета D1D к гипотенузе BD1. CosDD1B=√2/4
О