- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Прямоугольный треугольник (7 класс)
Содержание
- 1. Презентация по математике на тему Прямоугольный треугольник (7 класс)
- 2. Соотношения между сторонами и углами прямоугольного треугольникаТема урока:
- 3. Этапы урока1. Повторение пройденного материала2. Решение задач3. Самостоятельная работа4. Подведение итогов урока5. Домашнее задание
- 4. Определение прямоугольного треугольникаПовторение пройденного материала1 свойство прямоугольного треугольника2 свойство прямоугольного треугольника3 свойство прямоугольного треугольника
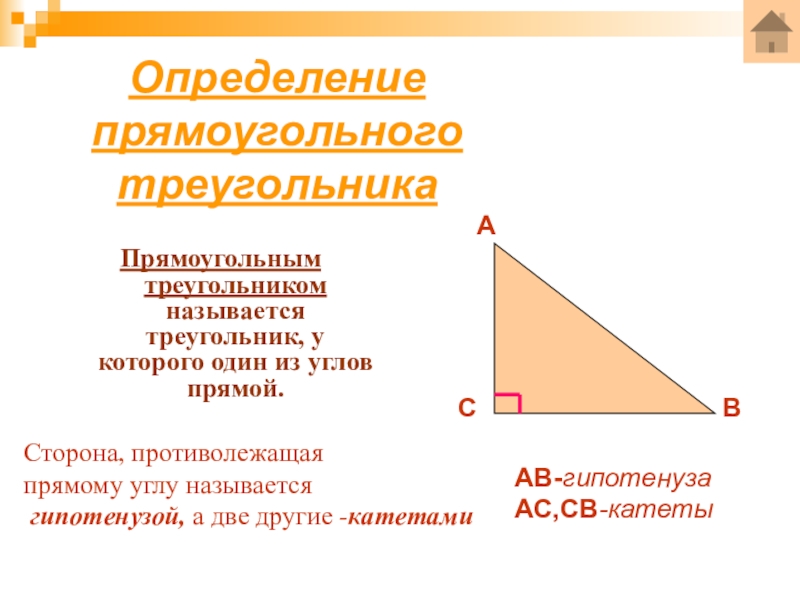
- 5. Определение прямоугольного треугольникаПрямоугольным треугольником называется треугольник, у
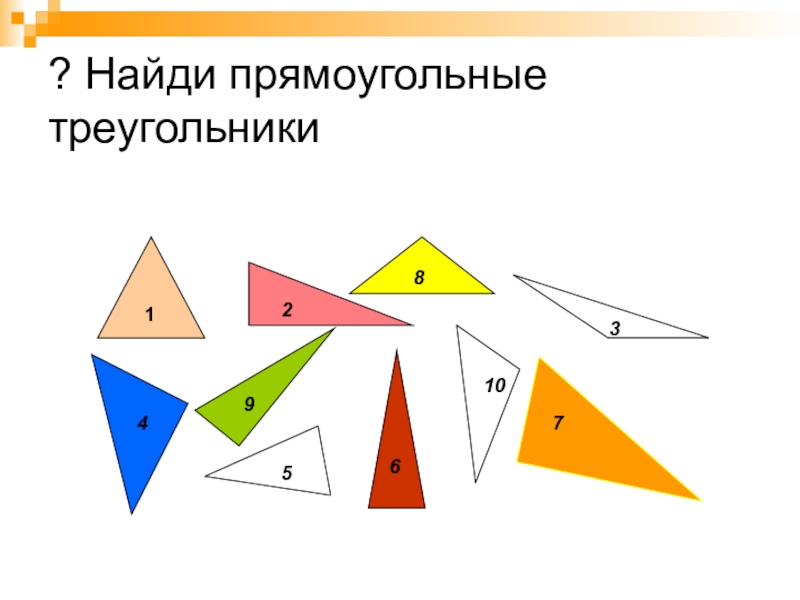
- 6. ? Найди прямоугольные треугольники12345678910
- 7. Гипотенуза и катетСлова «гипотенуза» и «катет» греческие.«Гипотенуза» -в переводе «натянутая»«Катет»-в переводе «отвес»
- 8. ?Найдите гипотенузу и катетыАВ СDАВСDОКD-высотаМNКD
- 9. ? Найдите острый угол200300450700600450
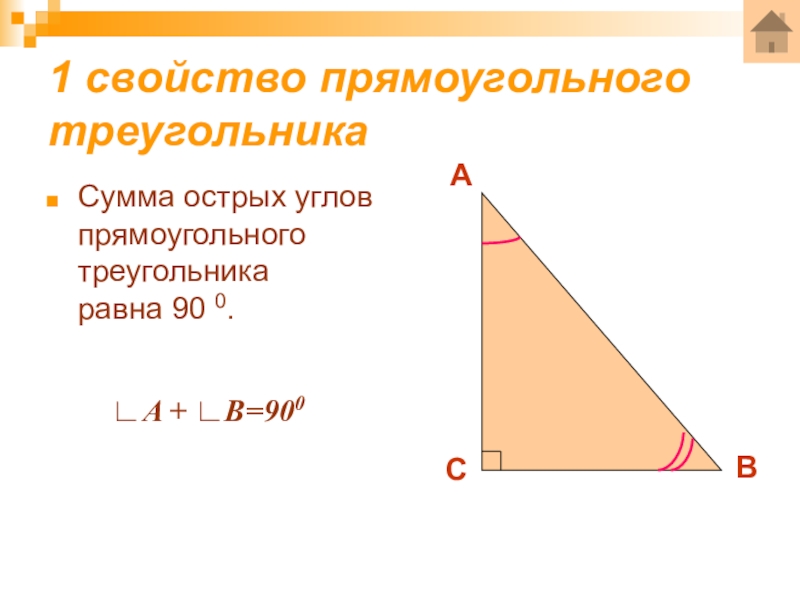
- 10. 1 свойство прямоугольного треугольникаСумма острых углов прямоугольного
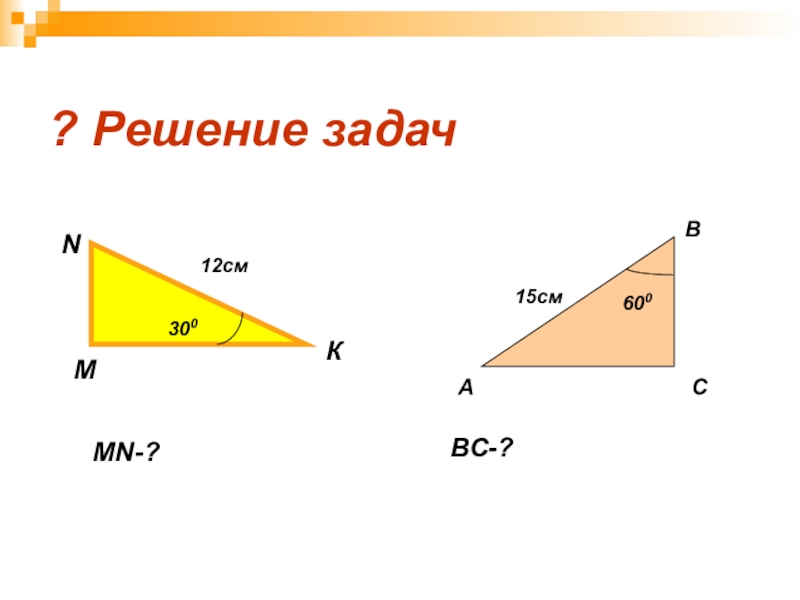
- 11. 12см30015см600? Решение задачАВСВС-?МNКMN-?
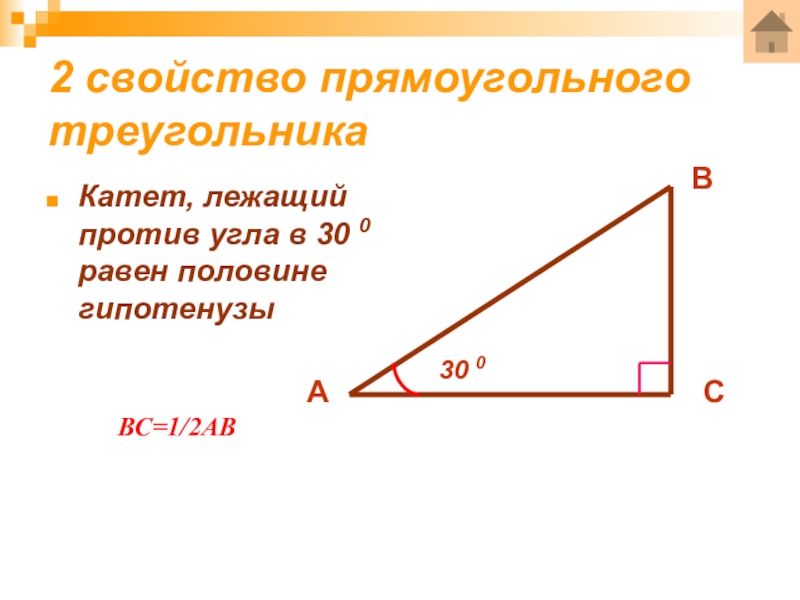
- 12. 2 свойство прямоугольного треугольникаКатет, лежащий против угла в 30 0 равен половине гипотенузыВС=1/2АВАВС30 0
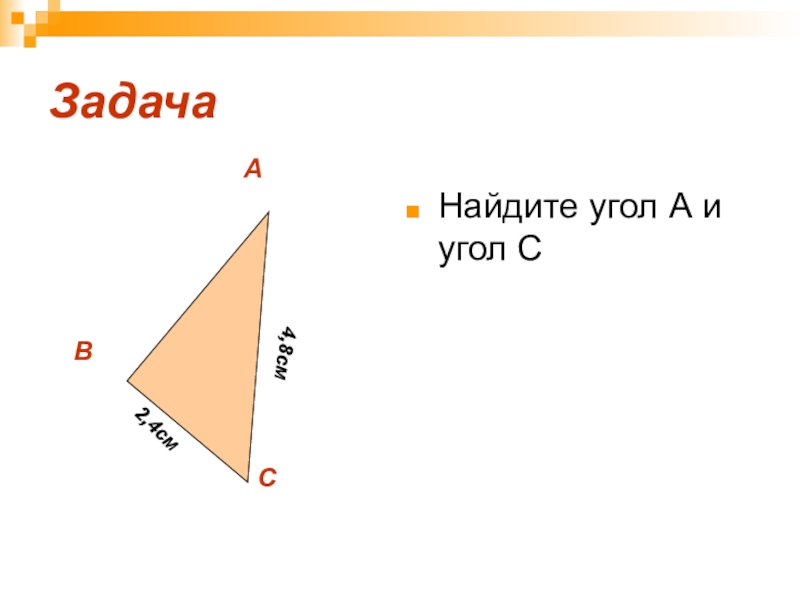
- 13. ЗадачаНайдите угол А и угол САВС2,4см4,8см
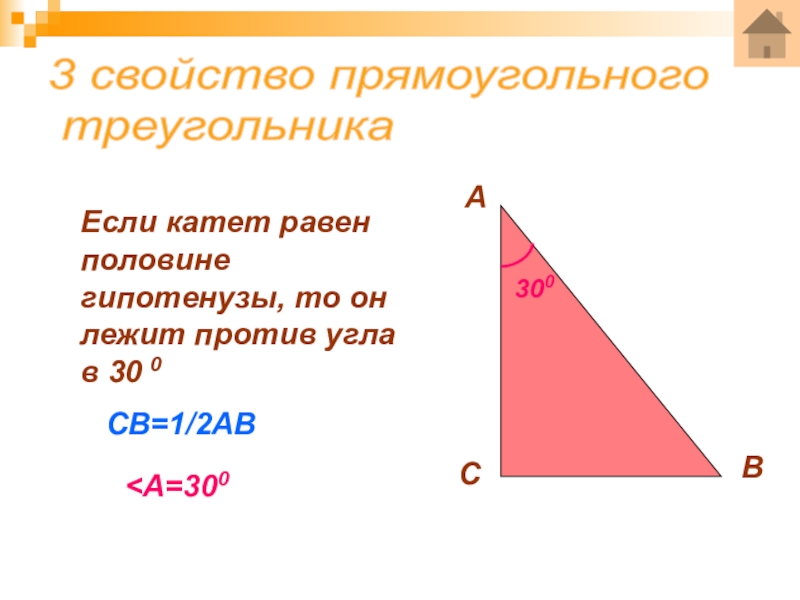
- 14. 3 свойство прямоугольного треугольникаАСВЕсли катет
- 15. Прямоугольный треугольник∆АВС-прямоугольный ∟С=900 АВСАС-катет,противолежащий углу ВСВ-катет, прилежащий углу ВАВ-гипотенуза
- 16. Определение синуса острого углаСинусом острого угла
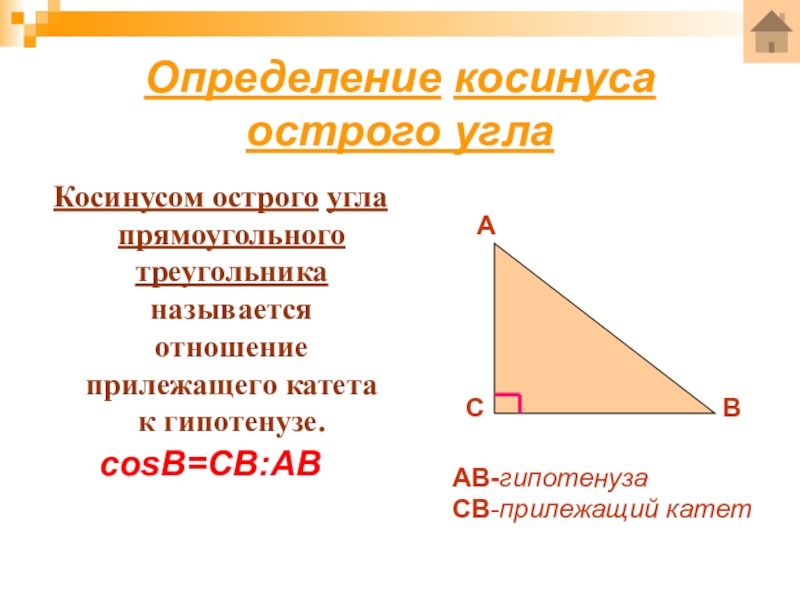
- 17. Определение косинуса острого углаКосинусом острого угла
- 18. Определение тангенса острого углаТангенсом острого угла
- 19. Решить задачу
- 20. Синус острого угла Синусом острого угла прямоугольного
- 21. Синус острого угла САВ
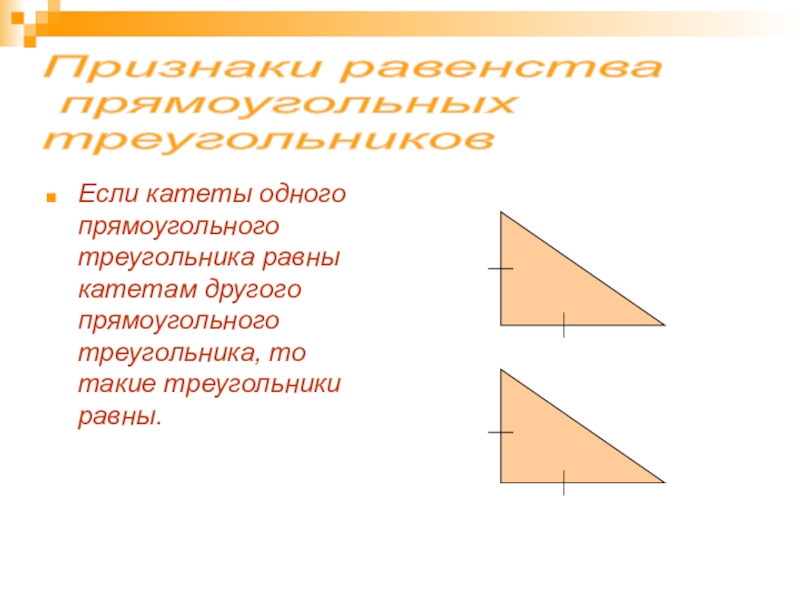
- 22. Признаки равенства прямоугольных треугольниковЕсли
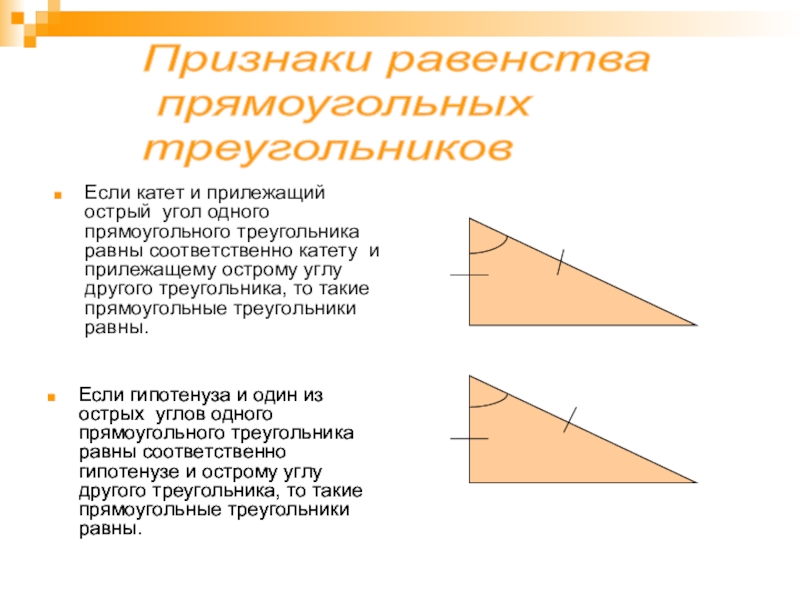
- 23. Если гипотенуза и один из острых углов
- 24. Если гипотенуза и катет одного прямоугольного треугольника
- 25. Признаки равенства прямоугольных треугольников
- 26. ? Найдите пары равных треугольников и докажите их равенство.
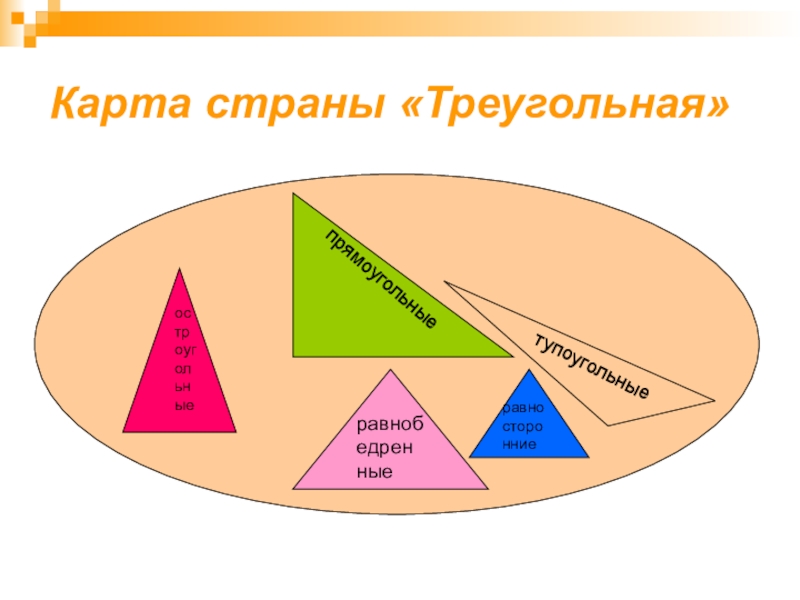
- 27. Карта страны «Треугольная»прямоугольныеостроугольныетупоугольныеравносторонниеравнобедренные
- 28. Задача 1. В треугольнике АВС угол С
- 29. Подведение итогов урокаЗадача 1Задача 2
- 30. Решение задачи 1Рассмотрим треугольник СС1В-прямоугольный. По условию
- 31. Решение задачи 2Доказательство:По условию СВ=АД, АВ- общая гипотенуза, значит ∆АВС= ∆ АВД (по гипотенузе и катету),тогда∟САВ=∟ДВА.АВСД
- 32. Домашнее задание
- 33. Открытая математика 2.6. Планиметрия.При разработке презентации были использованы:Математика 5-11. Практикум.
Слайд 1Геометрия
8 класс
Габдракипова Л.Р.,
учитель математики МКОУ «Усть-Багарякская средняя общеобразовательная школа»
Слайд 3Этапы урока
1. Повторение пройденного материала
2. Решение задач
3. Самостоятельная работа
4. Подведение итогов
5. Домашнее задание
Слайд 4Определение прямоугольного треугольника
Повторение пройденного материала
1 свойство прямоугольного треугольника
2 свойство прямоугольного треугольника
3
Слайд 5Определение прямоугольного треугольника
Прямоугольным треугольником называется треугольник, у которого один из углов
А
В
С
Сторона, противолежащая
прямому углу называется
гипотенузой, а две другие -катетами
АВ-гипотенуза
АС,СВ-катеты
Слайд 7Гипотенуза и катет
Слова «гипотенуза» и «катет» греческие.
«Гипотенуза» -в переводе «натянутая»
«Катет»-в переводе
Слайд 101 свойство прямоугольного треугольника
Сумма острых углов прямоугольного треугольника
∟A + ∟B=900
А
С
В
Слайд 122 свойство прямоугольного треугольника
Катет, лежащий против угла в 30 0 равен
ВС=1/2АВ
А
В
С
30 0
Слайд 143 свойство прямоугольного
треугольника
А
С
В
Если катет равен половине гипотенузы, то он
СВ=1/2АВ
<А=300
300
Слайд 15Прямоугольный треугольник
∆АВС-прямоугольный
∟С=900
А
В
С
АС-катет,противолежащий углу В
СВ-катет, прилежащий углу В
АВ-гипотенуза
Слайд 16Определение синуса
острого угла
Синусом острого угла прямоугольного треугольника называется отношение противолежащего
А
В
С
АВ-гипотенуза
АС-противолежащий катет
sinB=AC:AB
Слайд 17Определение косинуса
острого угла
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего
А
В
С
cosB=СВ:АВ
АВ-гипотенуза
СВ-прилежащий катет
Слайд 18Определение тангенса
острого угла
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего
А
В
С
tg B=AC:BC
АС-противолежащий катет
СВ-прилежащий катет
Слайд 20Синус острого угла
Синусом острого угла прямоугольного треугольника
∟A + ∟B=900
А
С
В
Слайд 22Признаки равенства
прямоугольных
треугольников
Если катеты одного прямоугольного треугольника равны катетам
Слайд 23Если гипотенуза и один из острых углов одного прямоугольного треугольника равны
Признаки равенства
прямоугольных
треугольников
Если гипотенуза и один из острых углов одного прямоугольного треугольника равны соответственно гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.
Если катет и прилежащий острый угол одного прямоугольного треугольника равны соответственно катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны.
Слайд 24Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и
Признаки равенства
прямоугольных
треугольников
Слайд 27Карта страны «Треугольная»
прямоугольные
остроугольные
тупоугольные
равносторонние
равнобедренные
Слайд 28Задача 1. В треугольнике АВС угол С равен 900, СС1-высота,
Задача 2. Два прямоугольных треугольника АВС и АВД имеют общую гипотенузу АВ и лежат по разные стороны от неё. Известно, что АД=ВС. Докажите, что угол САВ равен углу ДВА.
для самостоятельного решения
Слайд 30Решение задачи 1
Рассмотрим треугольник СС1В-прямоугольный. По условию СС1=5см,СВ=10см,т.е.СС1=1/2СВ, значит ∟В=300,тогда
тогда ∟САВ=900-300=600
Ответ: 60º
С
С1
А
В
5см
10см
Слайд 31Решение задачи 2
Доказательство:По условию СВ=АД, АВ- общая гипотенуза, значит ∆АВС= ∆
∟САВ=∟ДВА.
А
В
С
Д