- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Пирамида 10 класс
Содержание
- 1. Презентация по математике на тему Пирамида 10 класс
- 2. Начало геометрии пирамиды было положено в
- 3. ПИРАМИДА (др.-греч. πυραμίς, род. п. πυραμίδος) —
- 4. Элементы пирамиды апофема — высота боковой грани
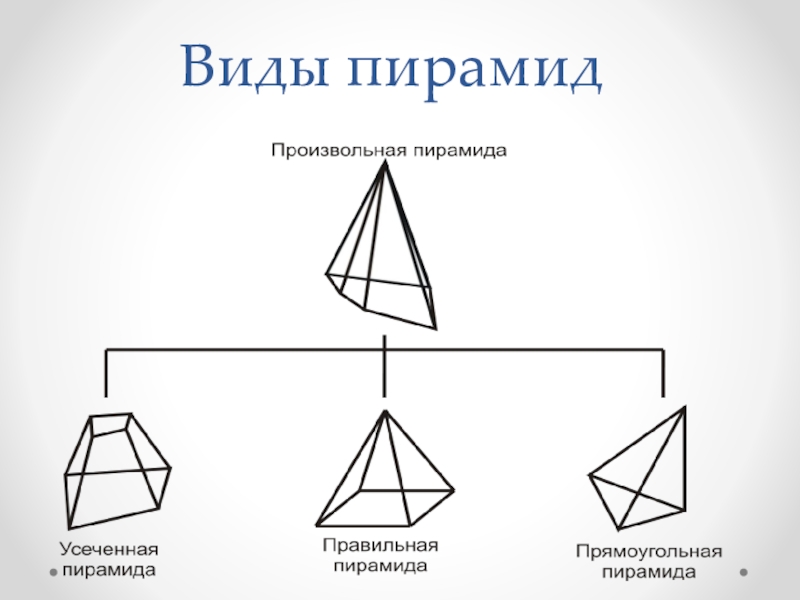
- 5. Виды пирамид
- 6. Особые случаи пирамиды
- 7. Слайд 7
- 8. Прямоугольная Пирамида называется прямоугольной, если одно из
- 9. Тетраэдр Тетраэдром называется треугольная пирамида. В тетраэдре
- 10. Основные свойства правильной пирамиды Боковые ребра, боковые
- 11. Объем треугольной пирамиды равен 15. Плоскость проходит
- 12. Объем тетраэдра равен 200. Найдите объем многогранника,
- 13. Площадь поверхности тетраэдра равна 120. Найдите площадь
- 14. Ребра многогранника равны его половине ребра тетраэдра,
- 15. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИКакой многогранник называется пирамидой?Назовите вершину
- 16. СПАСИБО ЗА ВНИМАНИЕ!!!!!
Слайд 1Пирамиды
Презентация подготовлена учителем математики
МКОУ Русскогвоздевская СОШ
Богачевой Ниной Владимировной
Слайд 2 Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако
Слайд 3ПИРАМИДА (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, одна из граней
Слайд 4Элементы пирамиды апофема — высота боковой грани правильной пивккрамиды, проведённая из её
SO — высота
SF — апофема
OF — радиус вписанной в основание окружности
Слайд 8Прямоугольная Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно
Слайд 9Тетраэдр Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть
Слайд 10Основные свойства правильной пирамиды Боковые ребра, боковые грани и апофемы соответственно равны. Двугранные
Слайд 11Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой
Проанализируем объём какой пирамиды будет больше: EABC или SEBC?
*Объём пирамиды равен одной трети произведения площади её основания и высоты:
Если рассмотреть две полученные пирамиды и в обеих принять за основание грань ЕВС, то становится очевидно, то объём пирамиды АЕВС будет больше объёма пирамиды SEBC. Почему?
Расстояние от точки А до плоскости ЕВС больше чем расстояние от точки S. А это расстояние играет у нас роль высоты.
Итак, найдём объём пирамиды ЕАВС.
Объём исходной пирамиды нам дан, основание у пирамид SАВС и ЕАВС общее. Если мы установим соотношение высот, то без труда сможем определить объём.
Из отношения отрезков ES и AE следует, что АЕ равно две третьих ES. Высоты пирамид SАВС и ЕАВС находятся в такой же зависимости - высота пирамиды ЕАВС будет равна 2/3 высоты пирамиды SАВС.
Таким образом, если
То
Ответ: 10
Постоим пирамиду, обозначим вершины. Отметим на ребре AS точку Е, так чтобы AE была в два раза больше ES (в условии сказано, что ES относится к AE как 1 к 2), и построим указанную плоскость проходящую, через ребро АС и точку Е:
Слайд 12Объем тетраэдра равен 200. Найдите объем многогранника, вершинами которого являются середины
Объем указанного многогранника равен разности объемов исходного тетраэдра V0 и четырех равных тетраэдров, каждый из которых получается отсечением плоскостью, проходящей через середины рёбер, имеющих общую вершину:
Определим, чему равен объём отсеченного тетраэдра.
Отметим, что исходный тетраэдр и «отсечённый» тетраэдр являются подобными телами. Известно, что отношение объёмов подобных тел равно k3, где k - коэффициент подобия. В данном случае он равен 2 (так как все линейные размеры исходного тетраэдра в два раза больше соответствующих размеров отсечённого):
Вычислим объём отсечённого тетраэдра:
Таким образом, искомый объём будет равен:
Ответ: 100
Слайд 13Площадь поверхности тетраэдра равна 120. Найдите площадь поверхности многогранника, вершинами которого
Первый способ:
Искомая поверхность состоит из 8 равносторонних треугольников со стороной, вдвое меньшей ребра исходного тетраэдра. Поверхность исходного тетраэдра состоит из 16-ти таких треугольников (на каждой из 4 граней тетраэдра по 4 треугольника), поэтому искомая площадь равна половине площади поверхности данного тетраэдра и равна 60.
Второй способ:
Так как известна площадь поверхности тетраэдра, то мы можем найти его ребро, затем определить длину ребра многогранника и далее вычислить площадь его поверхности.
Площадь поверхности тетраэдра состоит из четырёх равных по площади правильных треугольников. Пусть сторона такого треугольника (ребро тетраэдра) равна а, тогда можем записать:
Слайд 14Ребра многогранника равны его половине ребра тетраэдра, то есть:
Они проходят через
Многогранник имеет восемь равных граней являющихся правильными треугольниками, значит его площадь поверхности будет равна:
Данное решение алгебраическое и рациональным его назвать никак нельзя, представлено как альтернативный вариант.
Ответ: 60
Слайд 15ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Какой многогранник называется пирамидой?
Назовите вершину пирамиды? Основание?
Какая пирамида называется
Куда проектируется высота правильной пирамиды?
Назовите угол между боковым ребром пирамиды и основанием; Между боковой гранью и основанием; угол между боковыми гранями пирамиды?