Э.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Пирамида (10 класс)
Содержание
- 1. Презентация по математике на тему Пирамида (10 класс)
- 2. Многогранник, составленный из n-угольника А1A 2…A n
- 3. Перпендикуляр, проведенный из вершины пирамиды к плоскости
- 4. Правильная пирамида Пирамида называется правильной, если ее основание
- 5. Высота боковой грани правильной пирамиды, проведенная из
- 6. Усеченная пирамида Плоскость, параллельная основанию пирамиды и пересекающая
- 7. Отрезки А1В1,А2В2, …АnВn называются боковыми ребрами усеченной
- 8. Правильная усеченная пирамидаP А1А2… Аn - правильная
- 9. Высота боковой грани правильной усеченной пирамиды называется
- 10. Решение задачЗадача №1. SABC – правильная треугольная
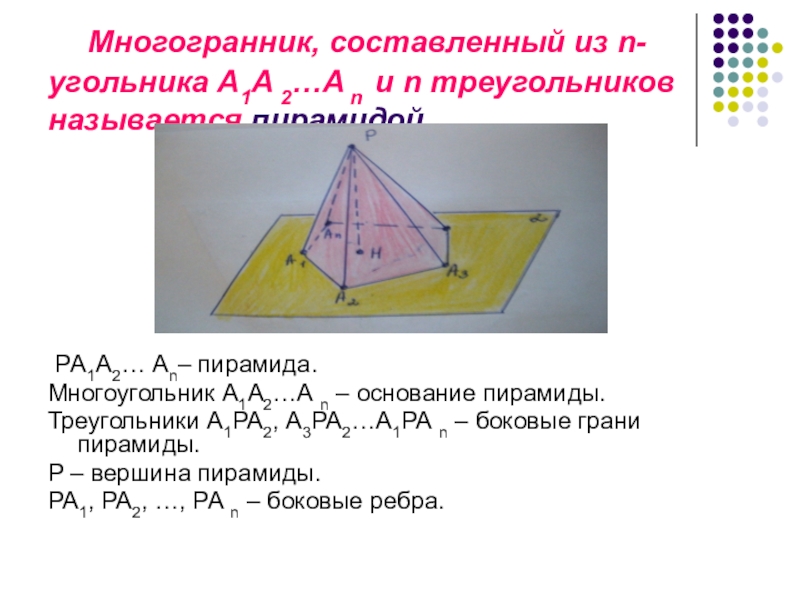
Многогранник, составленный из n-угольника А1A 2…A n и n треугольников называется пирамидой. PА1А2… Аn– пирамида.Многоугольник А1А2…А n – основание пирамиды.Треугольники А1РА2, А3РА2…А1РА n – боковые грани пирамиды.Р – вершина пирамиды.РА1, РА2, …, РА n – боковые
Слайд 2 Многогранник, составленный из n-угольника А1A 2…A n и n треугольников называется
пирамидой.
PА1А2… Аn– пирамида.
Многоугольник А1А2…А n – основание пирамиды.
Треугольники А1РА2, А3РА2…А1РА n – боковые грани пирамиды.
Р – вершина пирамиды.
РА1, РА2, …, РА n – боковые ребра.
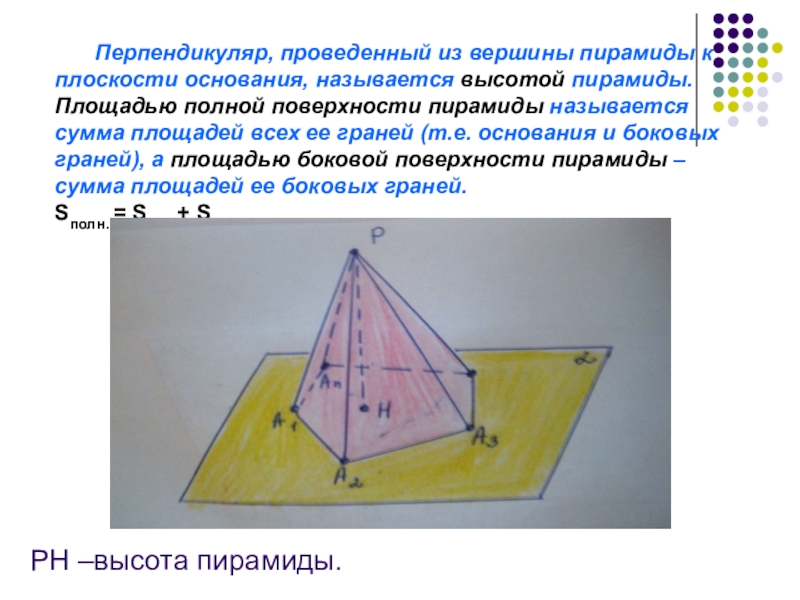
Слайд 3 Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т.е. основания и боковых граней), а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.
Sполн. = Sбок.+ Sосн.
РН –высота пирамиды.
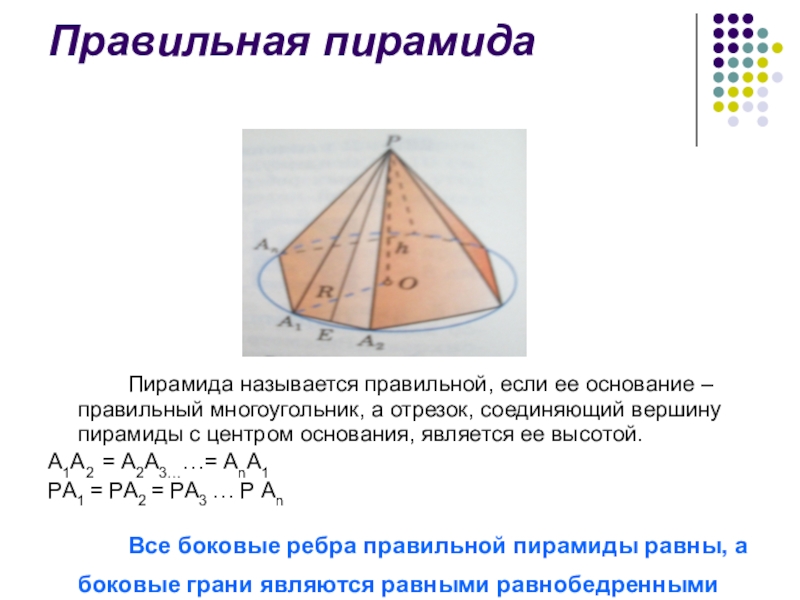
Слайд 4Правильная пирамида
Пирамида называется правильной, если ее основание – правильный многоугольник, а
отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
А1А2 = А2А3……= АnА1
PА1 = PА2 = PА3 … P Аn
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
А1А2 = А2А3……= АnА1
PА1 = PА2 = PА3 … P Аn
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Слайд 5 Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
РЕ
– апофема.
РЕ1= РЕ2= … = РЕn
Теорема. Площадь боковой поверхности пирамиды равна половине произведения периметра основания на апофему.
РЕ1= РЕ2= … = РЕn
Теорема. Площадь боковой поверхности пирамиды равна половине произведения периметра основания на апофему.
Слайд 6Усеченная пирамида
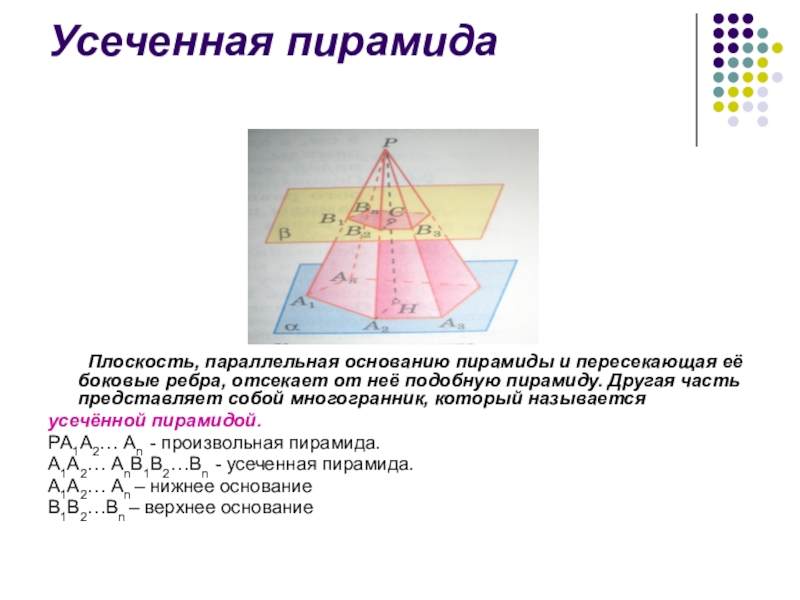
Плоскость, параллельная основанию пирамиды и пересекающая её боковые ребра, отсекает
от неё подобную пирамиду. Другая часть представляет собой многогранник, который называется
усечённой пирамидой.
PА1А2… Аn - произвольная пирамида.
А1А2… АnВ1В2…Вn - усеченная пирамида.
А1А2… Аn – нижнее основание
В1В2…Вn – верхнее основание
усечённой пирамидой.
PА1А2… Аn - произвольная пирамида.
А1А2… АnВ1В2…Вn - усеченная пирамида.
А1А2… Аn – нижнее основание
В1В2…Вn – верхнее основание
Слайд 7 Отрезки А1В1,А2В2, …АnВn называются боковыми ребрами усеченной пирамиды. Перпендикуляр, проведенный из какой-нибудь
точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды.
СН – высота усеченной пирамиды.
Боковые грани усеченной пирамиды – трапеции.
Слайд 8Правильная усеченная пирамида
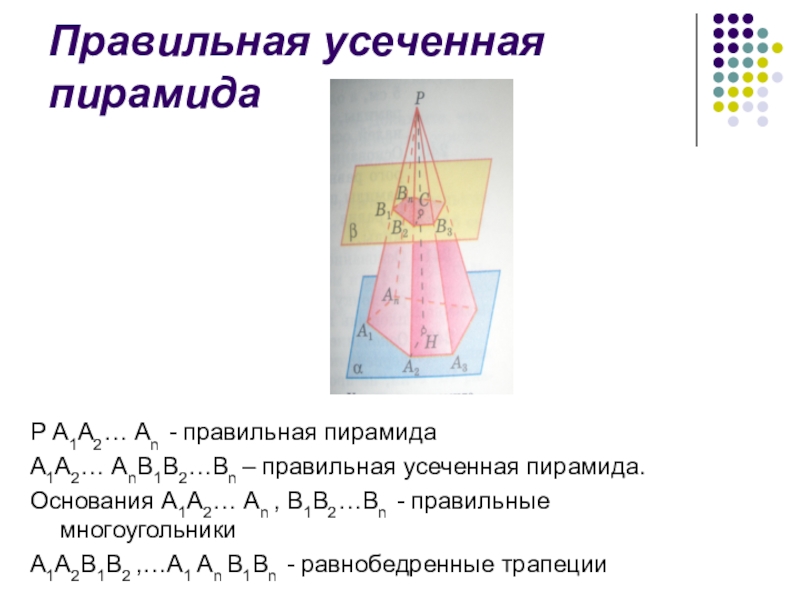
P А1А2… Аn - правильная пирамида
А1А2… АnВ1В2…Вn – правильная
усеченная пирамида.
Основания А1А2… Аn , В1В2…Вn - правильные многоугольники
А1А2В1В2 ,…А1 Аn В1Вn - равнобедренные трапеции
Основания А1А2… Аn , В1В2…Вn - правильные многоугольники
А1А2В1В2 ,…А1 Аn В1Вn - равнобедренные трапеции
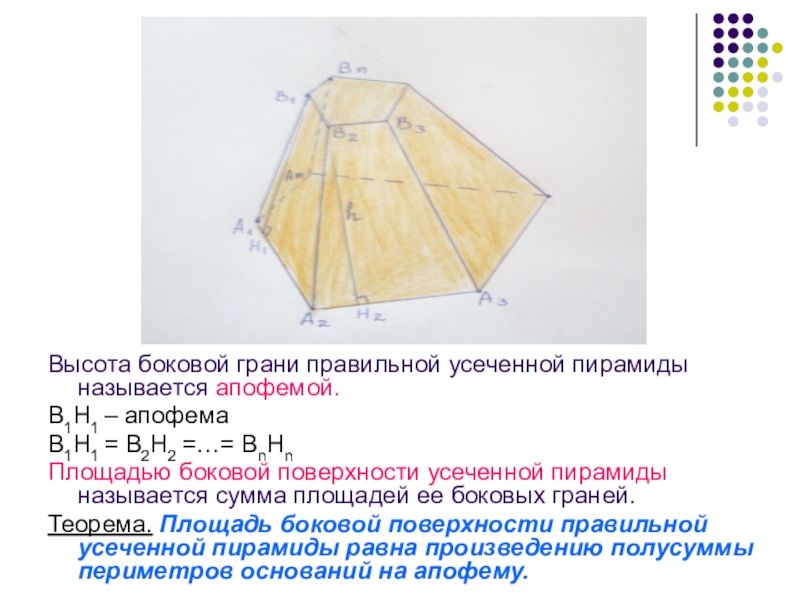
Слайд 9Высота боковой грани правильной усеченной пирамиды называется апофемой.
В1Н1 – апофема
В1Н1 =
В2Н2 =…= ВnНn
Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.
Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.
Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Слайд 10Решение задач
Задача №1. SABC – правильная треугольная пирамида.
АВ=3
SD – апофема
SD =
5
Sбок -?
Задача №2. PABCD – правильная четырехугольная пирамида.
АВ=6 см, высота РО=4 см.
Sполной пов. -?
Задача №3. Стороны оснований правильной треугольной пирамиды равны 6 см и 5 см. А апофема равна 7 см. Найдите площадь полной поверхности усеченной пирамиды.
Sбок -?
Задача №2. PABCD – правильная четырехугольная пирамида.
АВ=6 см, высота РО=4 см.
Sполной пов. -?
Задача №3. Стороны оснований правильной треугольной пирамиды равны 6 см и 5 см. А апофема равна 7 см. Найдите площадь полной поверхности усеченной пирамиды.